Chapter 5 因果推断
5.1 探寻可能的影响因素(经典先单因素后多因素分析,所有因素分析结果列入表格)
探索性影响因素研究,即探索对某个临床结局(事件)有影响的关联因素,属于病因学的范畴,探索对结局有影响的可能原因。
所谓”探索性”,是指研究开始没有固定某些感兴趣的影响因素,而是在一堆可能的因素里,探索性挖掘可能有意义的独立影响因素。
主要特点:
根据上传的科研数据,简单点击设置后,系统探寻结局的可能影响因素,遵循临床研究中常见的流程:先单因素(univariate)筛查 → 再多因素(multivariable)建模。
支持多种回归家族:
二分类结局:Logistic(输出 OR),Log-Binomial(输出 RR)
有序多分类结局:Ordered Logistic(输出 OR,支持 clm 与 polr)
连续结局:线性回归(输出回归系数 β)
生存结局:Cox 回归(输出 HR)
计数/率:Poisson(输出 IRR);Poisson+offset(适用于率、分数、比值)
自动合并单因素和多因素分析结果
支持人工纳入多因素变量、逐步回归纳入多因素变量
支持一键自动进行缺失数据多重填补(Multiple imputation)
支持一键自动把连续性变量拆分成分类变量
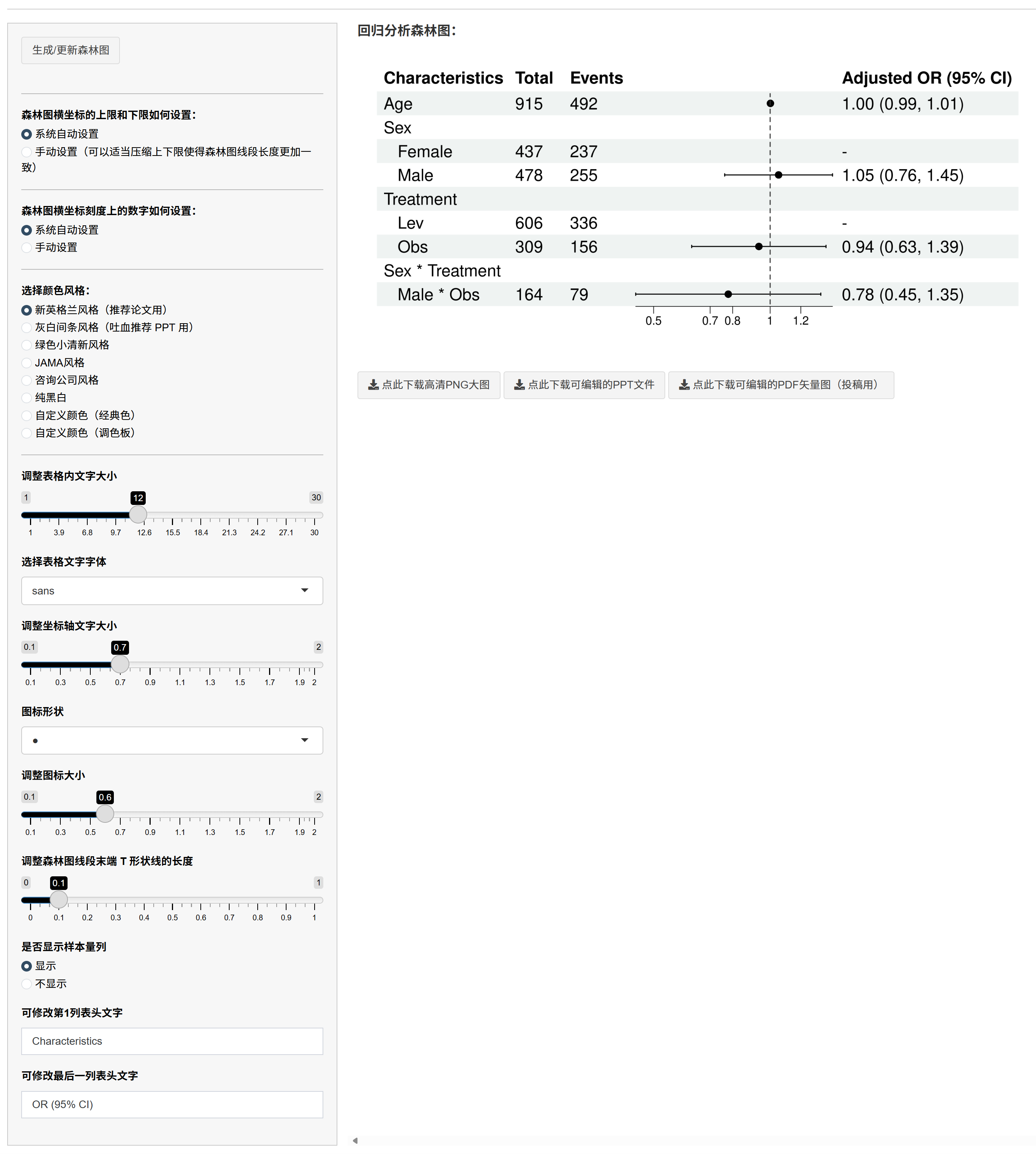
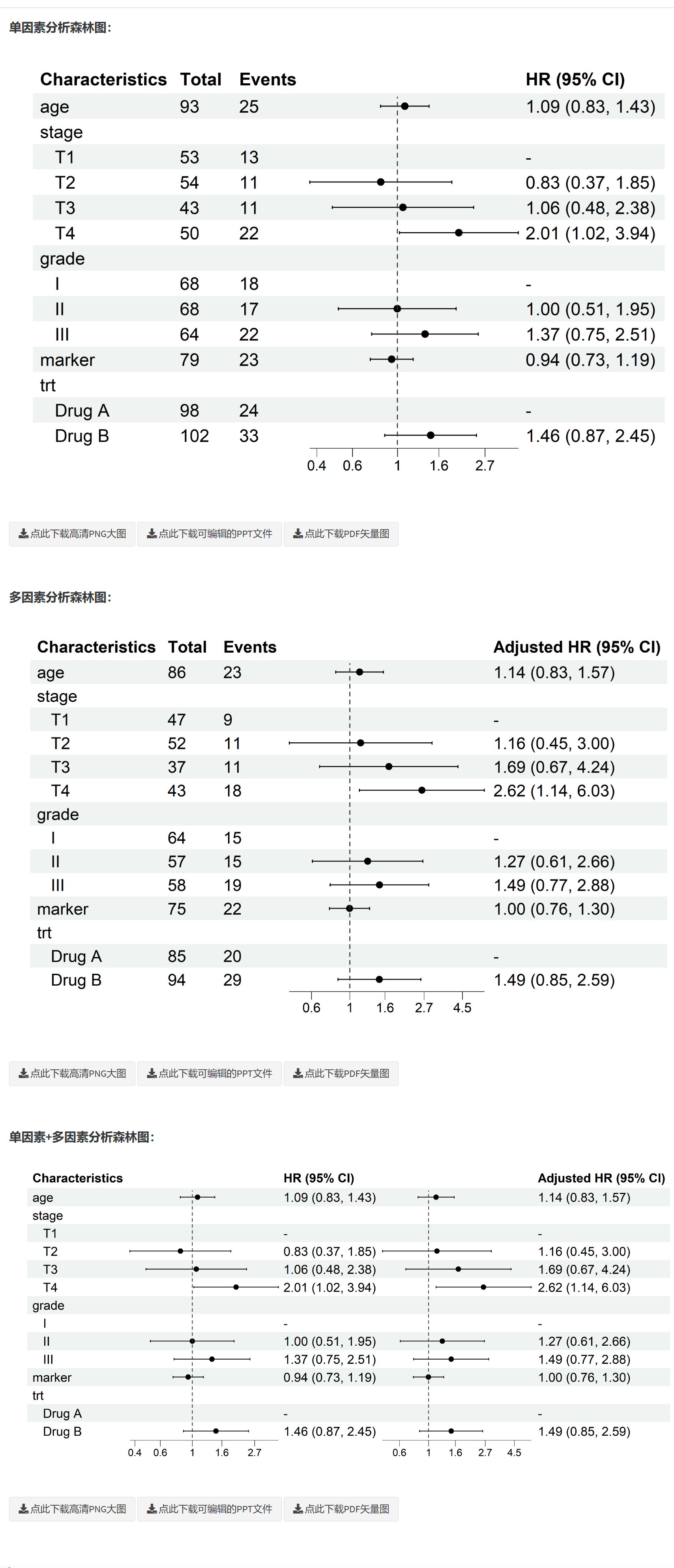
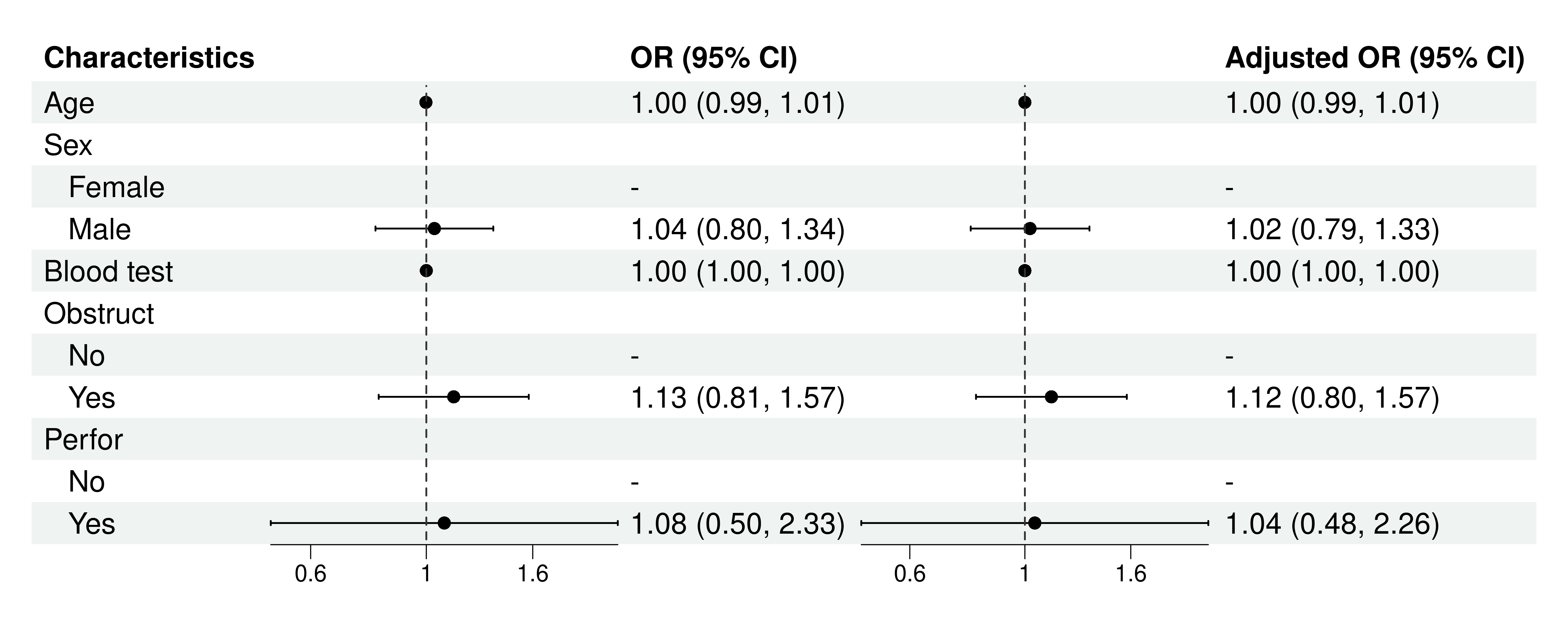
自动生成新英格兰医学杂志风格的华丽森林图
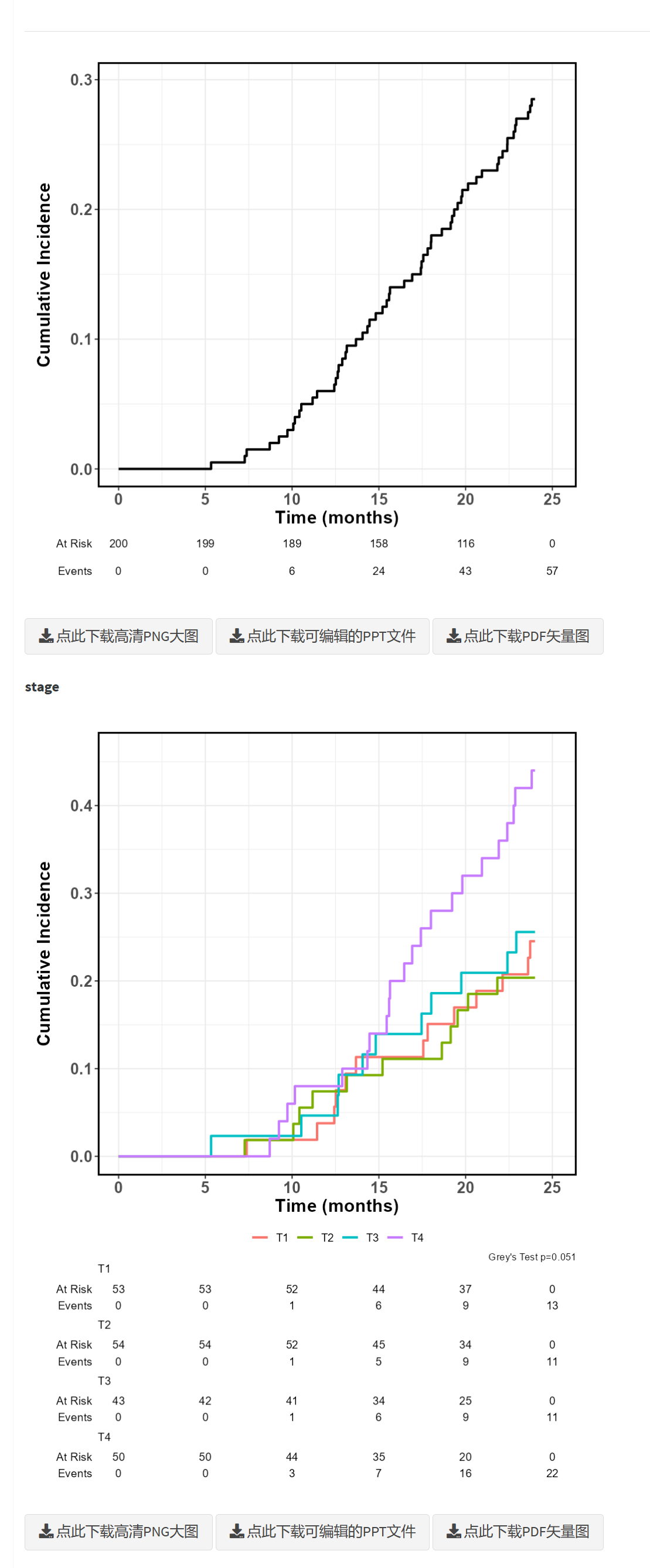
自动批量生成生存曲线图
生成 word 统计报告,自动生成 Title, Objective, Methods 和 Results, 生成 SCI 期刊标准统计表格
核心产物:投稿用表格(单因素/多因素/多重填补三栏合并)、回归系数表、拟合与共线性诊断、森林图、批量生存曲线、一键下载 Word/PPT 报告与可复现的 R 源代码。
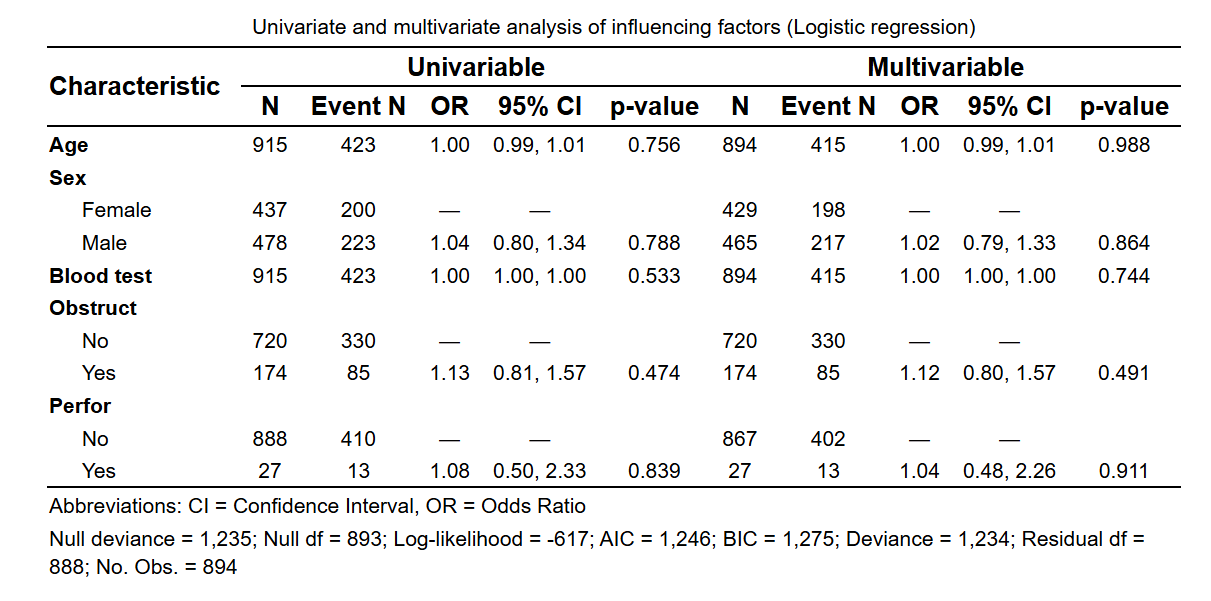
Logistic 回归:
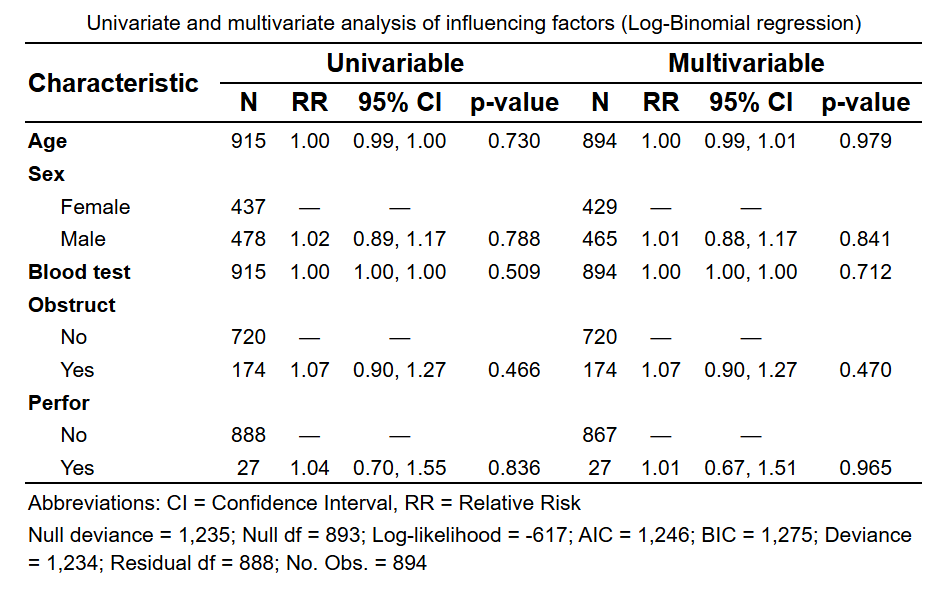
Log-Binomial 回归:
Linear 回归:
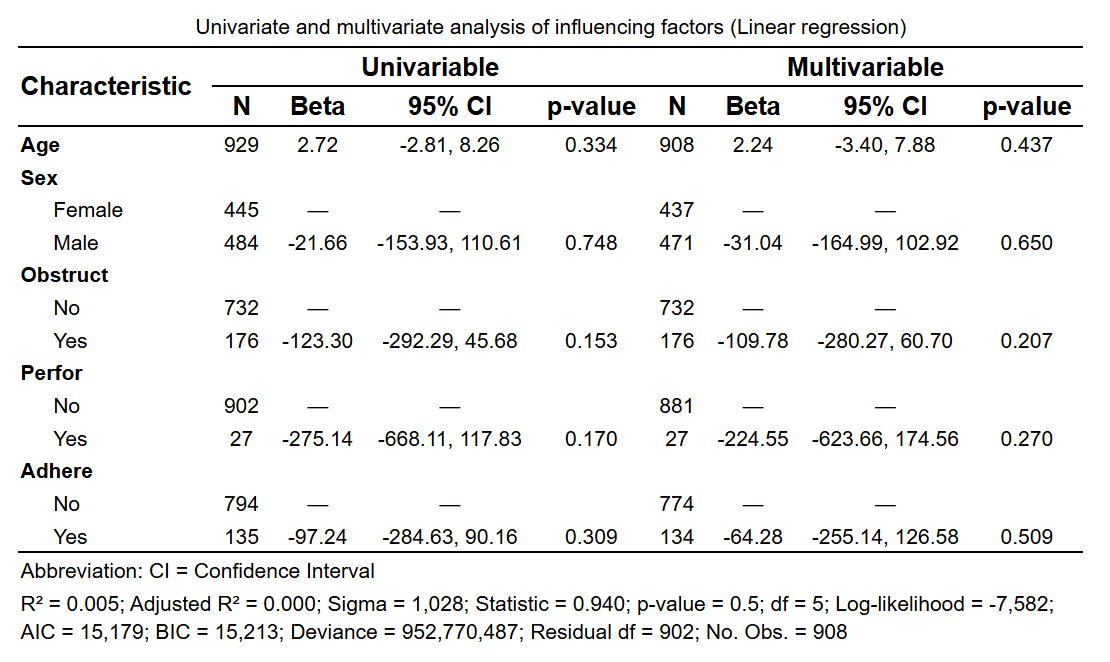
Cox 回归:
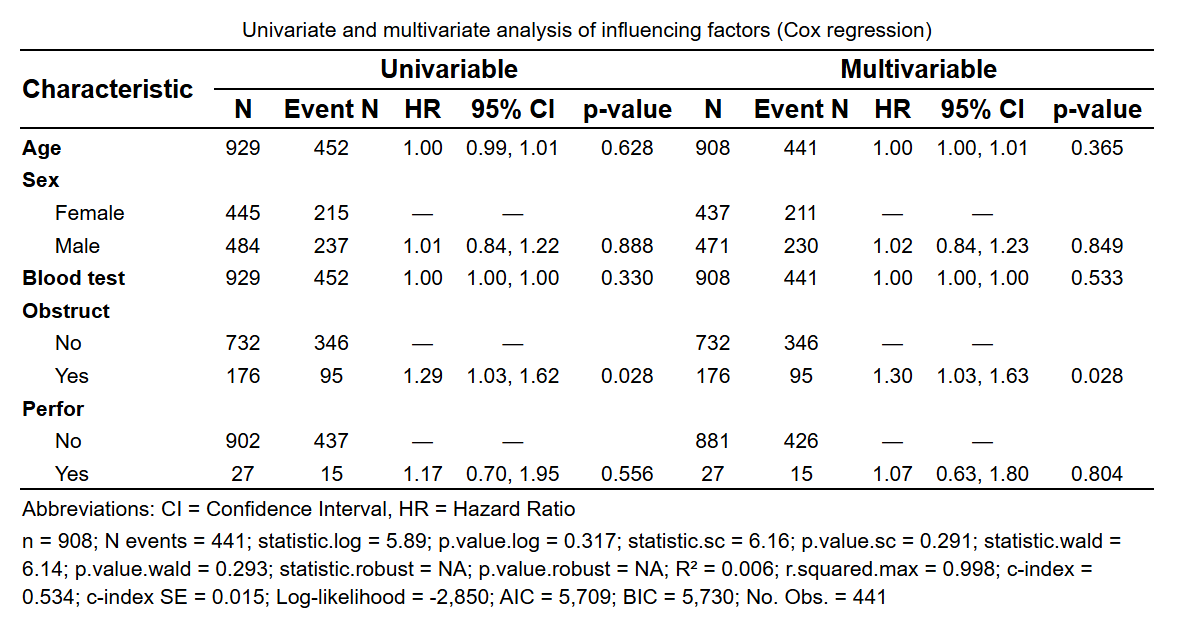
Poisson 回归:
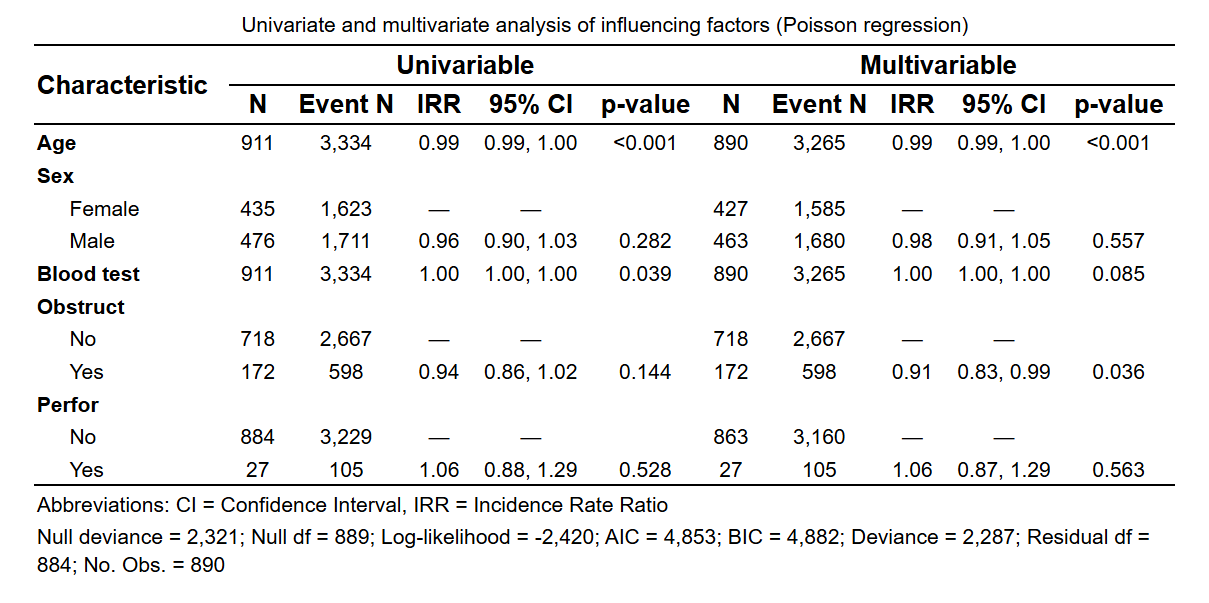
多重填补:
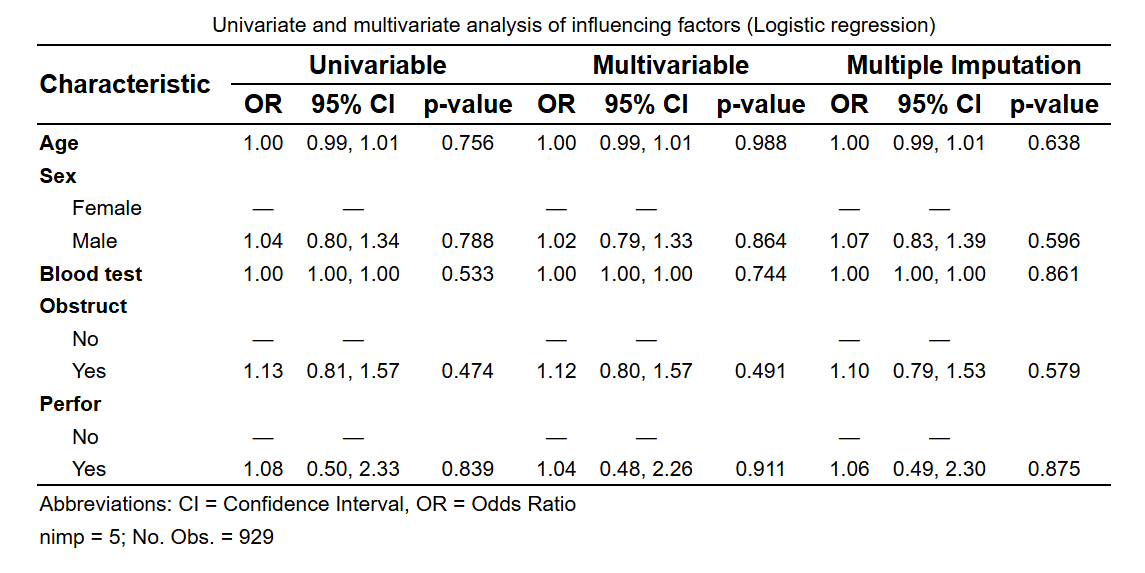
回归森林图:
5.1.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
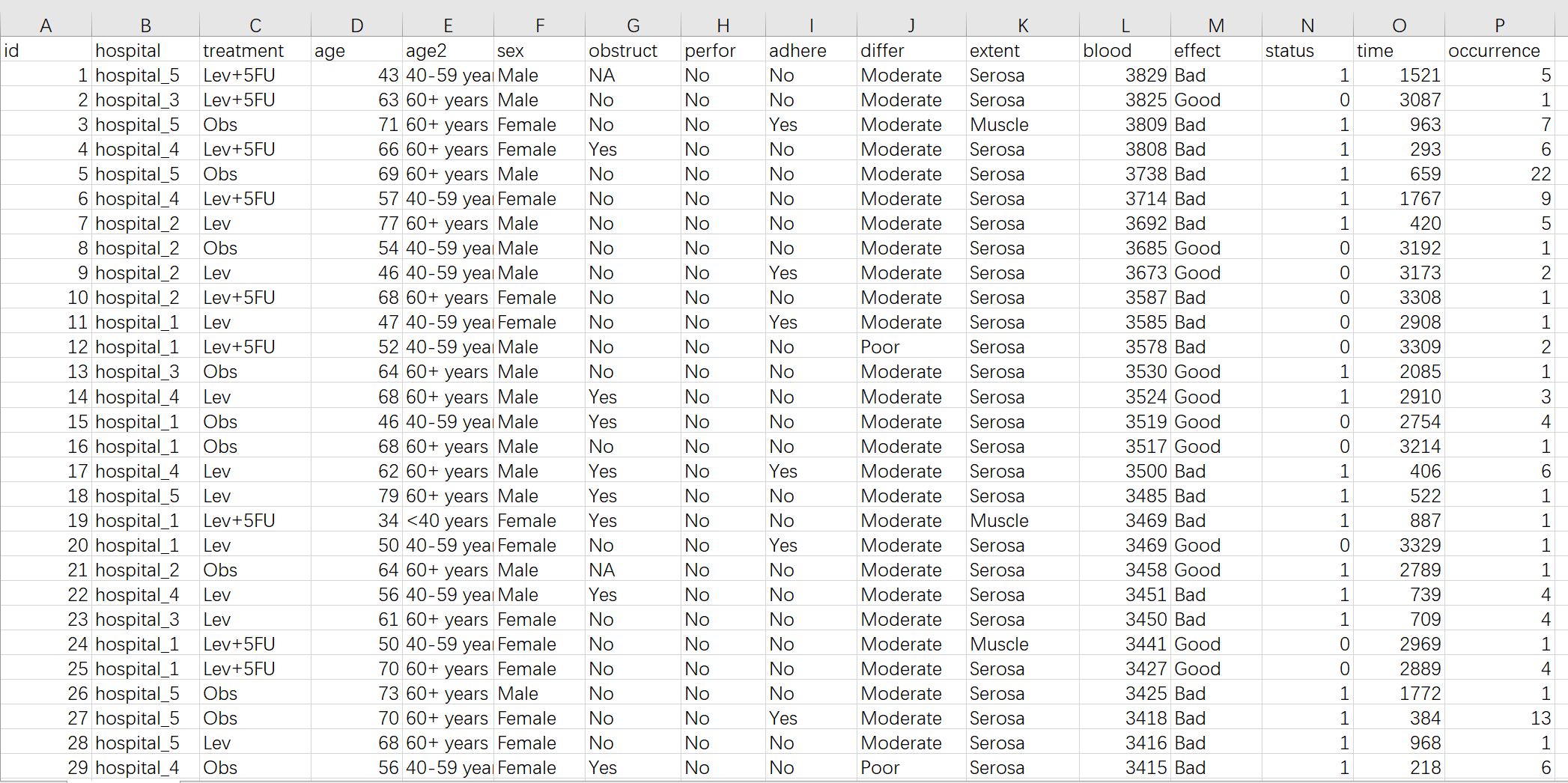
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量:
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的 effect(疗效)为二分类变量(Good,Bad)
有序分类结局变量
如本例中的 differ 为有序分类变量(Poor, Moderate, Well)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
5.1.3 前提条件
已在前面的 “数据导入/定义字段” 完成:变量类型设定、必要的重编码与命名(并点击应用更改直至按钮变绿)。
如需排除异常/限定亚组,建议先在 “患者筛选和亚组选择” 完成筛选。
结局变量准备:
Logistic/Log-Binomial:确保结局只有两个水平,并在本页明确选择“事件”所对应的水平。
Cox:提供 time(时间,数值型)与 status(状态,二分类;1=事件、0=删失),并在本页指定哪个水平为事件。
Poisson/offset:应变量(分子/计数)与 offset(分母)应为非负整数;分母>0。
5.1.4 页面结构与导航
本页包含 6 个页签(Tab):
使用说明。
单因素多因素分析:本模块的核心设置与表格输出。
生成森林图:基于回归结果绘制单因素/多因素森林图。
批量生成生存曲线:仅当上一步做的是生存分析时可用。
下载所有 Word 图表和统计报告:生成表格、图形、英文/中文报告、PPT。
查看 R 源代码和原始输出:导出可复现的数据与注释版源代码。
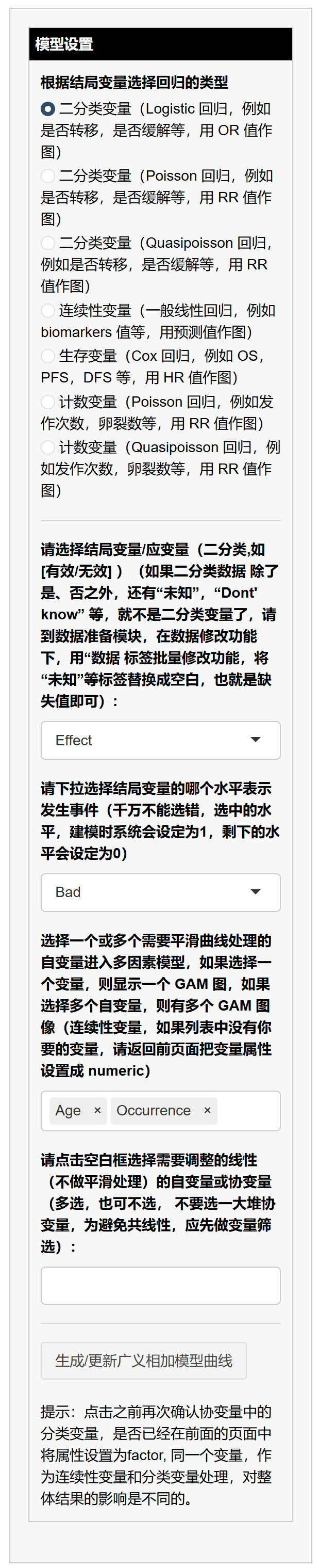
5.1.5 选择结局类型与模型(Family)
在左侧面板 “选择结局变量的类型及相应的模型种类”:
Logistic / Log-Binomial(二分类):先在 “应变量(二分类)” 选择结局,再在 “发生事件的水平” 指定哪一水平为“1(事件)”。
Ordered Logistic(有序多分类):先将结局在“定义字段”页设为有序因子(按从低到高排序),本页可在 clm/polr 两种实现间切换(推荐 clm,若报错可用 polr)。
Linear(连续):结局需为数值型。
Cox(生存):选择 time 与 status 两列,并在 “发生事件的水平” 指定事件值。
Poisson(计数):选择非负整数的应变量。
Poisson+offset(率/比):分别选择分子与分母(系统自动取
log(分母)作为 offset)。
务必注意: - “发生事件的水平”选错,会导致 OR/HR/RR/IRR 方向完全相反。 - Poisson/offset 中,分子与分母不能是同一变量;分母需为正数。
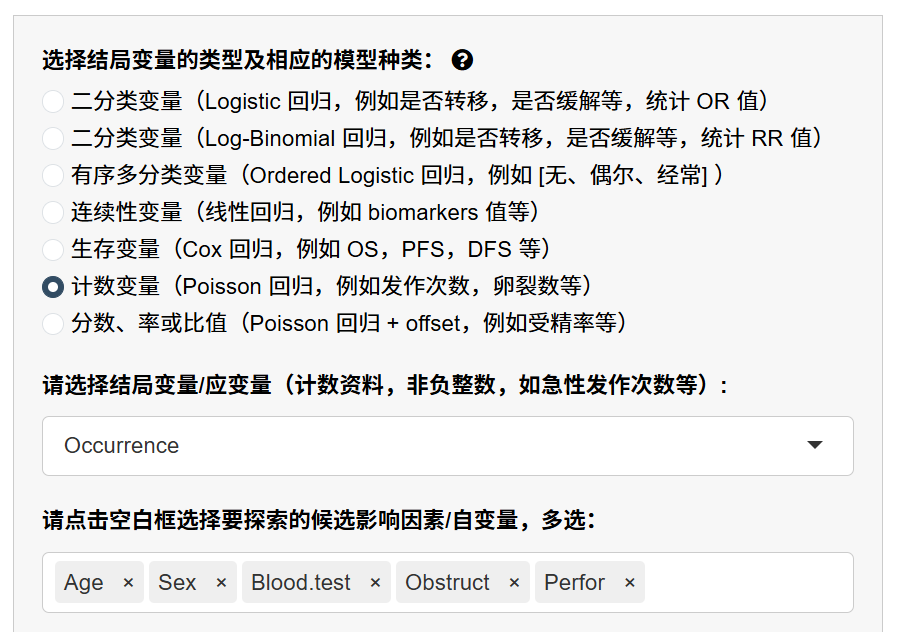
5.1.6 选择候选自变量(Explanatory)
在 “候选影响因素/自变量” 中多选变量。系统自动:
排除没有变异(只有一个水平)或全缺失的变量;
对字符型/高水平数的变量做合理过滤;
Cox 会自动排除
time/status;offset 会排除分子/分母。
若某变量在因变量缺失删行后只剩单一取值,会被自动排除。
5.1.7 多因素纳入策略(Multi-method)
Full model:全部候选变量进入多因素(注意 EPV ≈ 事件数/变量数 ≥ 10)。
Reduced model(推荐):基于文献与专业知识手工勾选进入多因素的变量。
按单因素 P 值筛选(不推荐):仅纳入单因素 P < 阈值(如 0.05/0.1)的变量。
逐步回归(stepAIC, backward):从全模型开始按 AIC 后退筛选,可在 “强制入选” 中指定必保留变量(如年龄、性别)。
经验提示:逐步回归结果不稳定、对样本敏感;推荐先用“因果推断/自动筛选”模块完成稳健筛选,再回到此处用 Reduced model 手工指定。

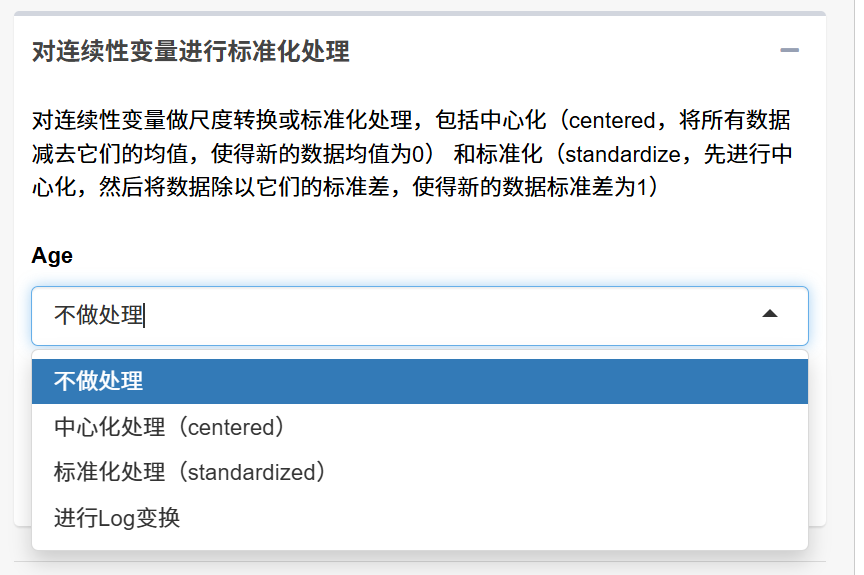
5.1.9 连续变量的处理
标准化/变换:在 “对连续性变量进行标准化处理” 中为每个数值型变量按需选择:
不处理 / 中心化(减去均值)/ 标准化(中心化后除以标准差)/ log 变换。
按分位数离散化(可选):勾选 “将连续性变量根据分位数转换成 n 等分”,选择待转换变量与分组数(常用 2–4 组),可选择是否显示切点范围。

提醒:将连续变量分组会损失信息、降低功效,除非确有临床意义或用于图表展示,一般不建议过度分箱。
5.1.10 缺失值处理(可选:多重插补 MI)
勾选 “对自变量缺失值进行多重填补”,设定 seed 与数据集个数 m(默认 5)。系统会:
通过
mice生成多套数据、分别建模并自动合并(pool)估计;合并结果在第三栏“Multiple Imputation”中展示,同时提供合并后的拟合指标表(glance)。
重要:若勾选 MI,不要再选择 profile likelihood CI(该方法对 MI 无效)。

5.1.11 表格展示与统计选项
置信区间:
Wald(与传统软件一致)或profile likelihood(更精确,勿与 MI 同用)。是否显示 N/Event、是否附加模型拟合指标(glance 底注)。
分类自变量 P 值类型:每个亚组 vs 参照组的 P(哑变量法,期刊常见)或 Global P。
P 值展示:原始 P / P+星号 / 仅星号。
小数位:效应量
digits与 P 值p_digits。设置完毕,点击 “生成/更新影响因素分析表” 执行分析。

5.1.12 查看与解读结果
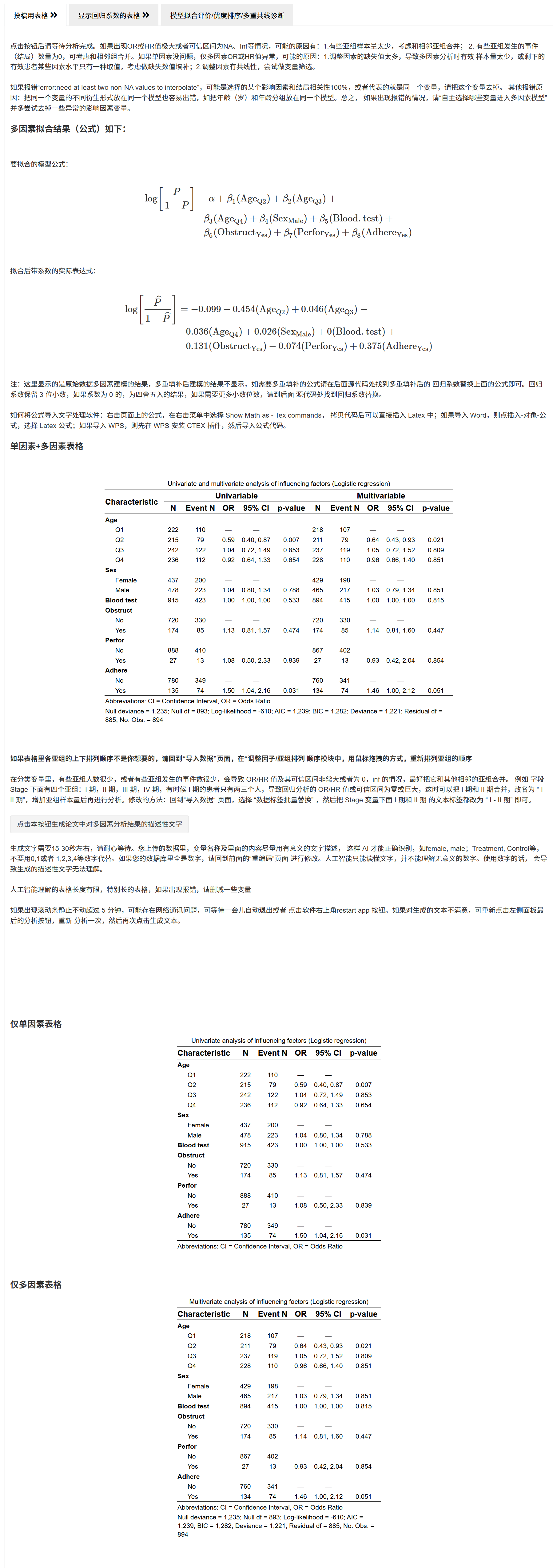
投稿用表格:左栏单因素,中栏多因素,若启用 MI,右栏显示 多重填补 结果。若 OR/HR/IRR 极大或 CI 为 NA/Inf,请参考“问题排查”。
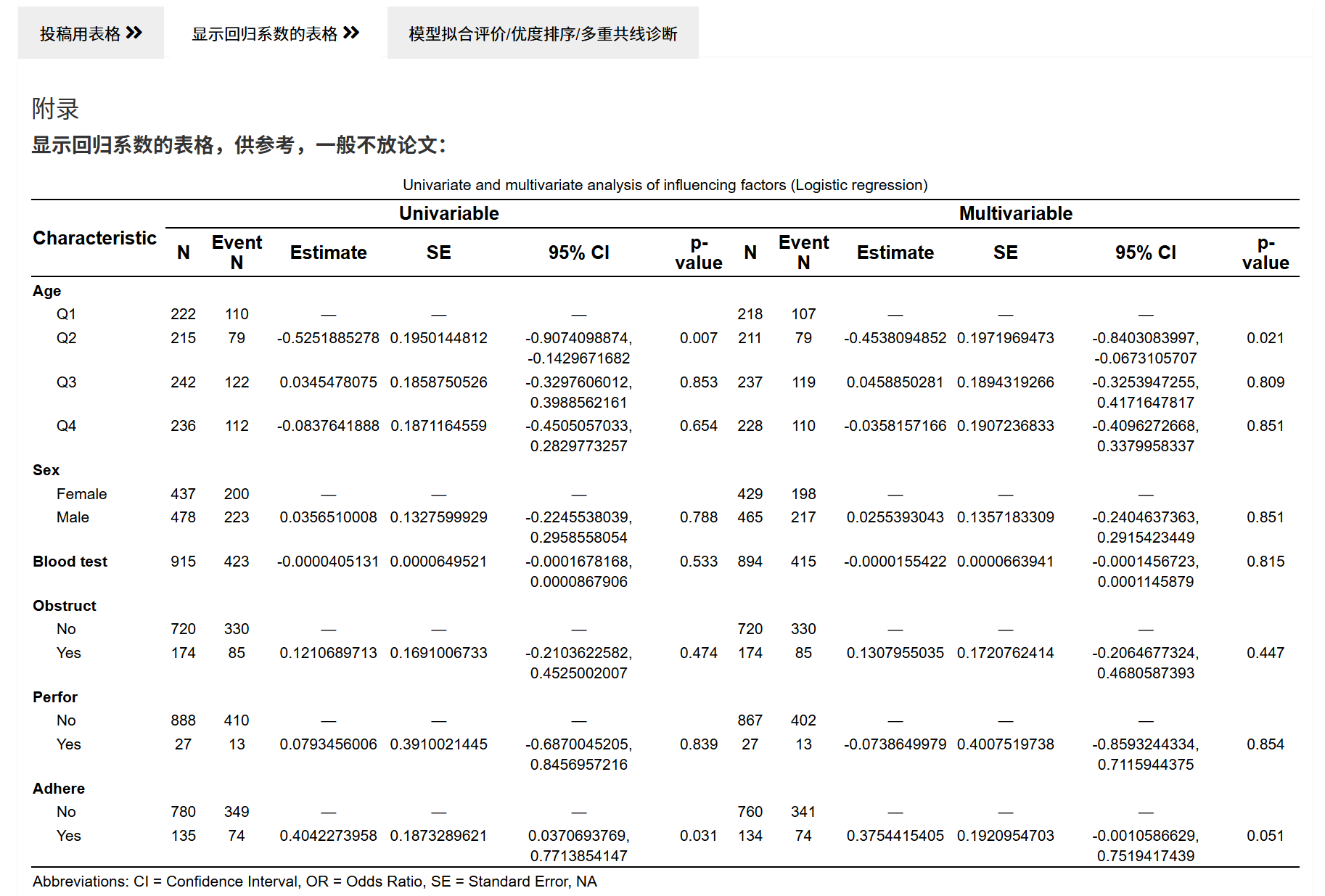
显示回归系数的表格:输出估计值与标准误等(便于附录/补充材料)。
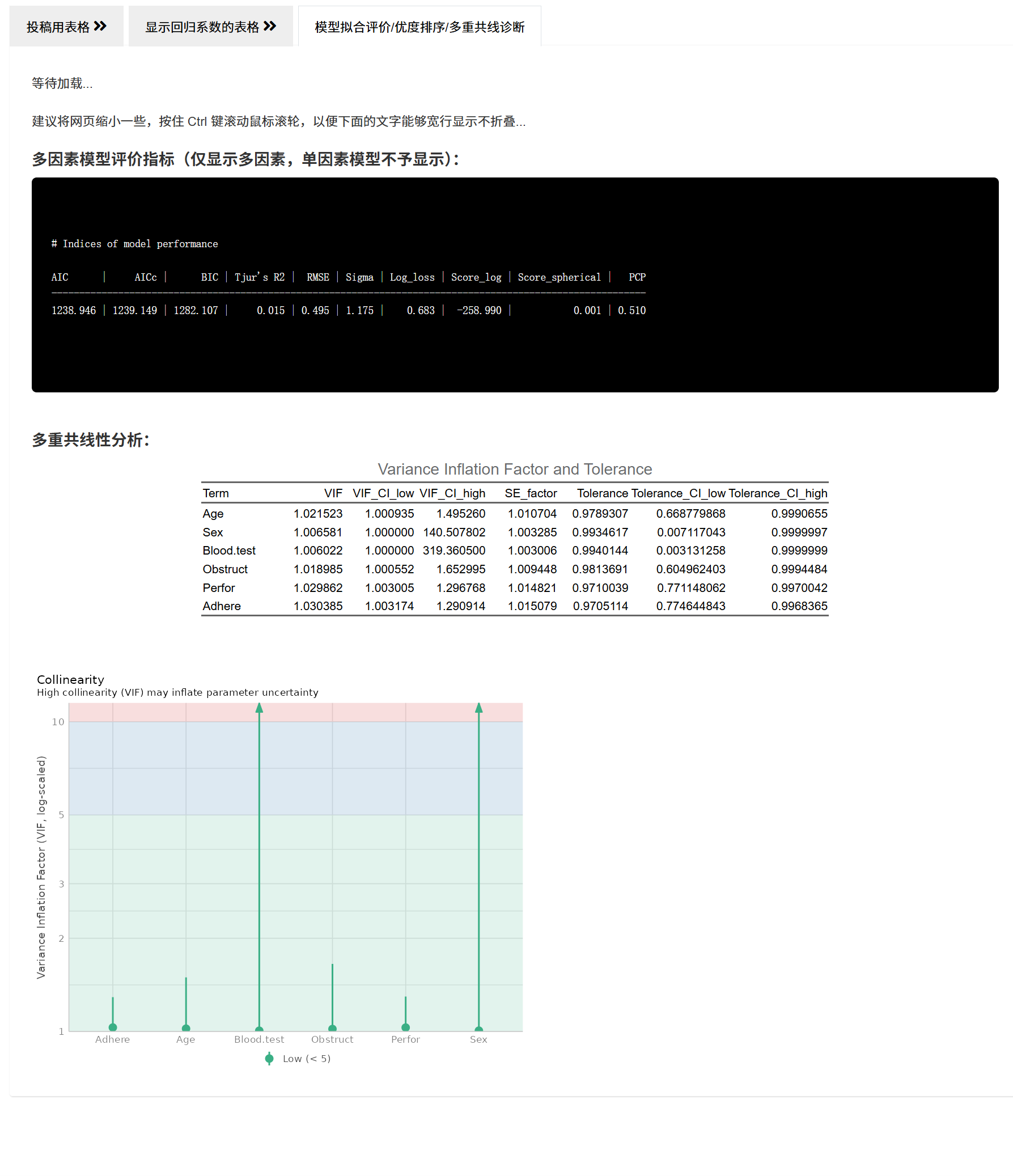
模型拟合评价/优度排序/多重共线诊断:展示
glance系列指标;Ordered Logistic 的 clm 另有专门的拟合表。
5.1.13 生成森林图
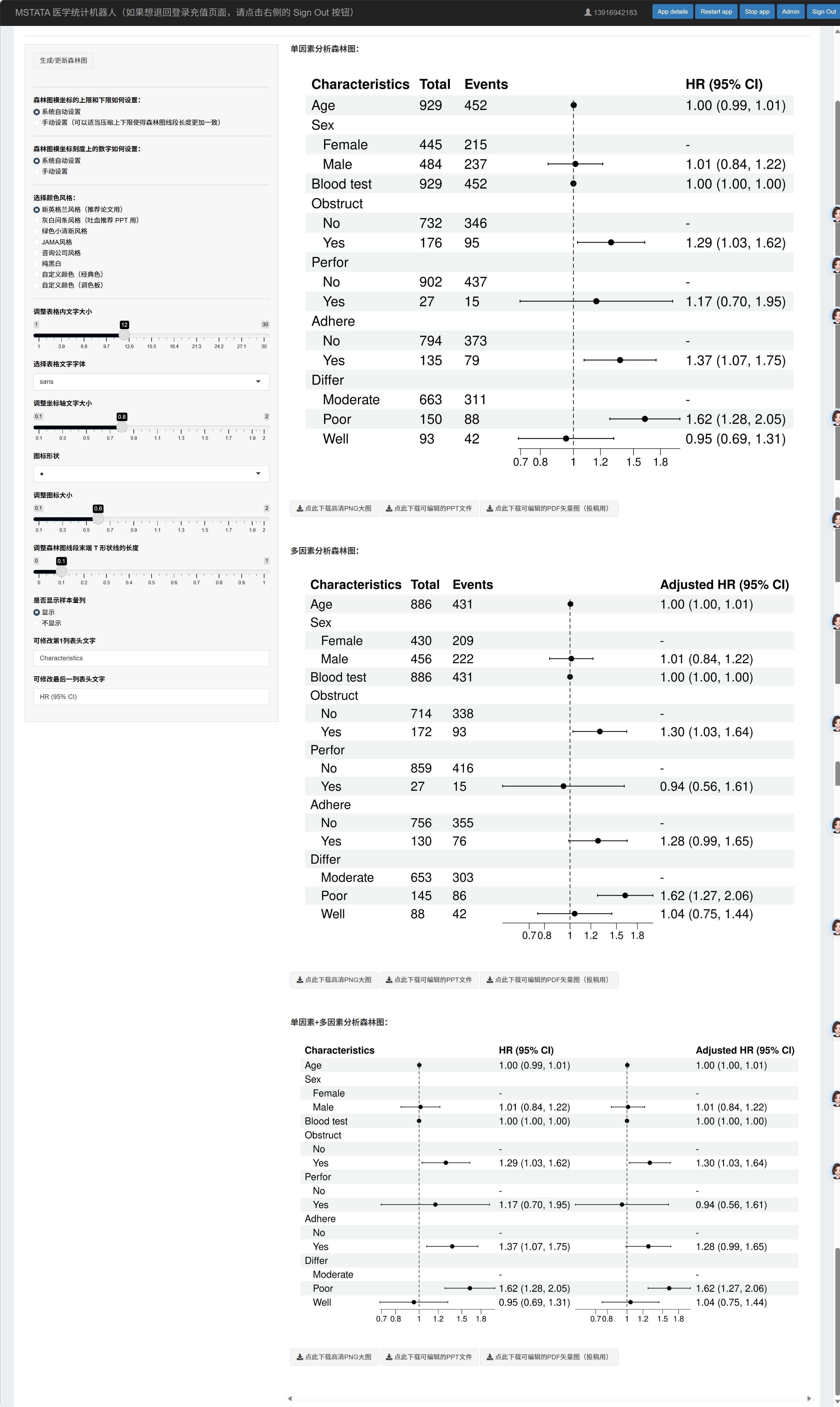
进入 “生成森林图”:
点击按钮分别生成单因素与多因素森林图(MI 时会提供合并后图)。
若图中 OR/HR/IRR 或其 CI 出现极大(>999)或极小(≈0),坐标会被压缩,请在左侧手动设置横轴上下限(如 0.1–10)与刻度。
若结果出现 0 或 Inf,系统会自动将其截断为极小/极大值以便绘图,并用带箭头的线表示越界;此时亦需手动设置坐标。
5.1.14 批量生成生存曲线(仅生存分析)
确认上一页选择的是 Cox。
选择时间单位与换算(1 年=365.25 天,1 月=30.4375 天)。
点击 “生成/更新生存曲线” 预览;根据需要调节图像宽高与字体、X 轴最小刻度等,直至不拥挤。
右击图片可另存为 PNG。
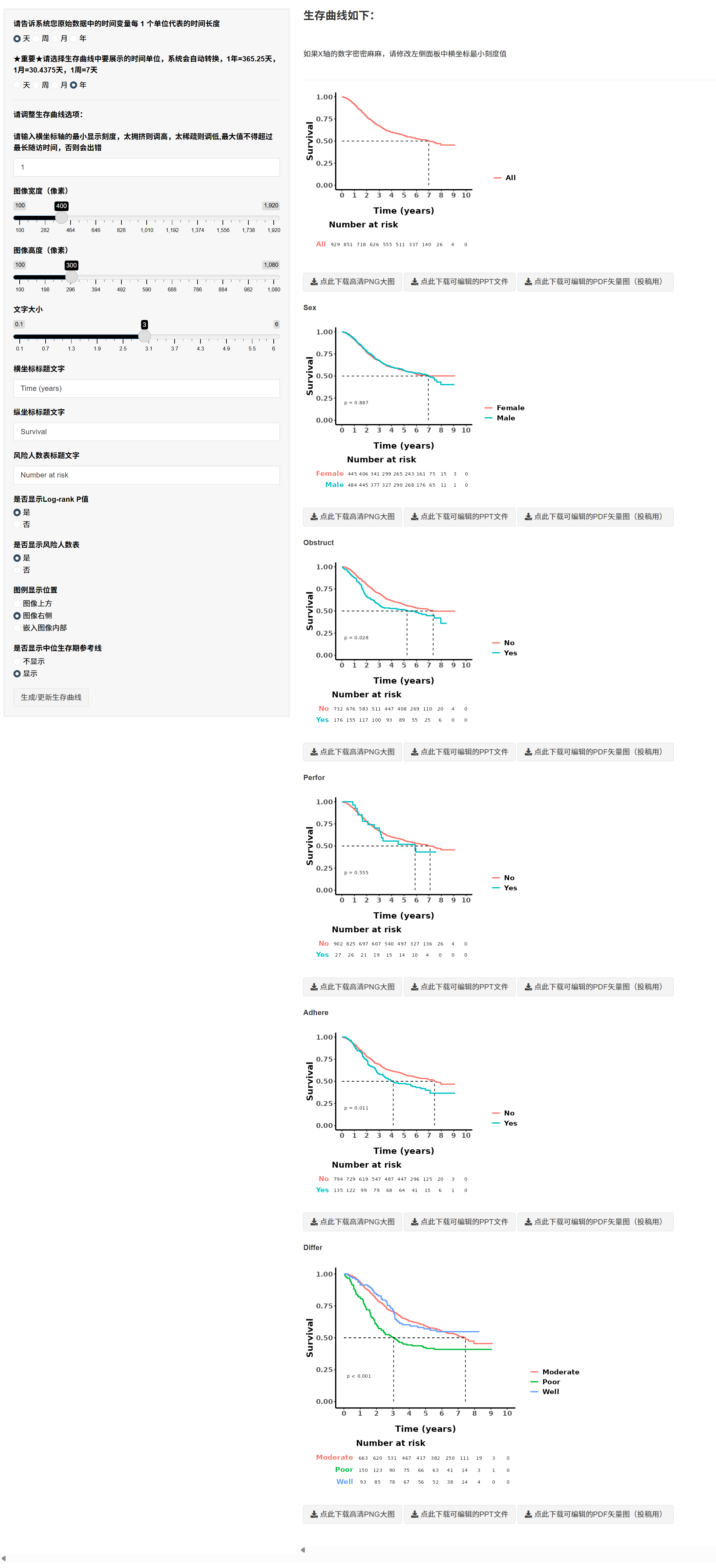
5.1.15 下载:表格、报告与 PPT
在 “下载所有 Word 图表和统计报告”:
仅图表(速度快):下载 Word 版表格与图。
英文/中文统计报告(含标题、方法、软件版本、结果描述、表图):
- 英文报告(推荐);中文报告为辅助(可能有个别用语不够地道)。
- 重要提示:若数据库仍用 0/1 表示“否/是”、1/2 表示“男/女”,请先回到重编码改成有意义的文字,否则自动撰写部分将难以阅读。
PPT 报告:英文/中文两种(适合汇报)。
报告生成需时间,请等待下载完成;建议用 Microsoft Word 打开,WPS 可能导致表头与脚注错位。

5.1.16 R 源代码与可复现性
在 “查看 R 源代码和原始输出”:
先点击 下载
data_frame.RData,在 R 中load('你的下载路径/data_frame.RData')或直接双击用 RStudio 打开。选择源代码注释语言(中文/英文),点击 下载 R 源代码文件。
重要:下载代码前,请保持本模块选项固定不再改动,否则代码与数据不一致会报错。

5.1.17 常见问题与排查
OR/HR/IRR 极端或 CI 为 NA/Inf:
亚组样本太少 → 合并相邻水平;
某亚组事件数为 0 → 合并水平或更换参照组;
多因素时有效样本骤减(因协变量缺失多)→ 考虑 多重填补;
协变量间共线性严重 → 变量筛选/降维;
Log-Binomial 不收敛时可改用 Logistic 报 OR。
“need at least two non-NA values to interpolate”:
- 某自变量与结局完美相关/重复信息,或同一变量的不同衍生形态同时入模(如
age与age_group同时进入);去掉其中之一。
- 某自变量与结局完美相关/重复信息,或同一变量的不同衍生形态同时入模(如
Ordered Logistic 报错:
- 尝试在 clm/polr 间切换;确认结局为有序因子且顺序正确。
Poisson/offset 报错:
- 确认应变量/分母均为非负整数且分母>0;避免将同一列同时作为分子与分母。
Cox 报错:
time为正数;status明确事件水平;避免负时间或全删失。
MI 与 CI 方法冲突:
- 启用 MI 时,请使用 Wald CI,不要选 profile likelihood。
5.1.18 质量核对清单(提交前必看)
结局类型选择正确,并已指定事件水平(Logistic/Cox)。
分类自变量均已设定合适参照组,稀有水平已适度合并。
连续变量是否被不必要地离散化?若已分组,是否同时保留原始连续变量用于建模或敏感性分析?
EPV 原则:事件数/自变量数 ≥ ~10,避免过拟合;共线性已检查。
Poisson/offset:分子/分母为非负整数,分母>0。
报告前核对:CI 方法、P 值展示方式、小数位、是否显示 N/Event 与拟合指标。
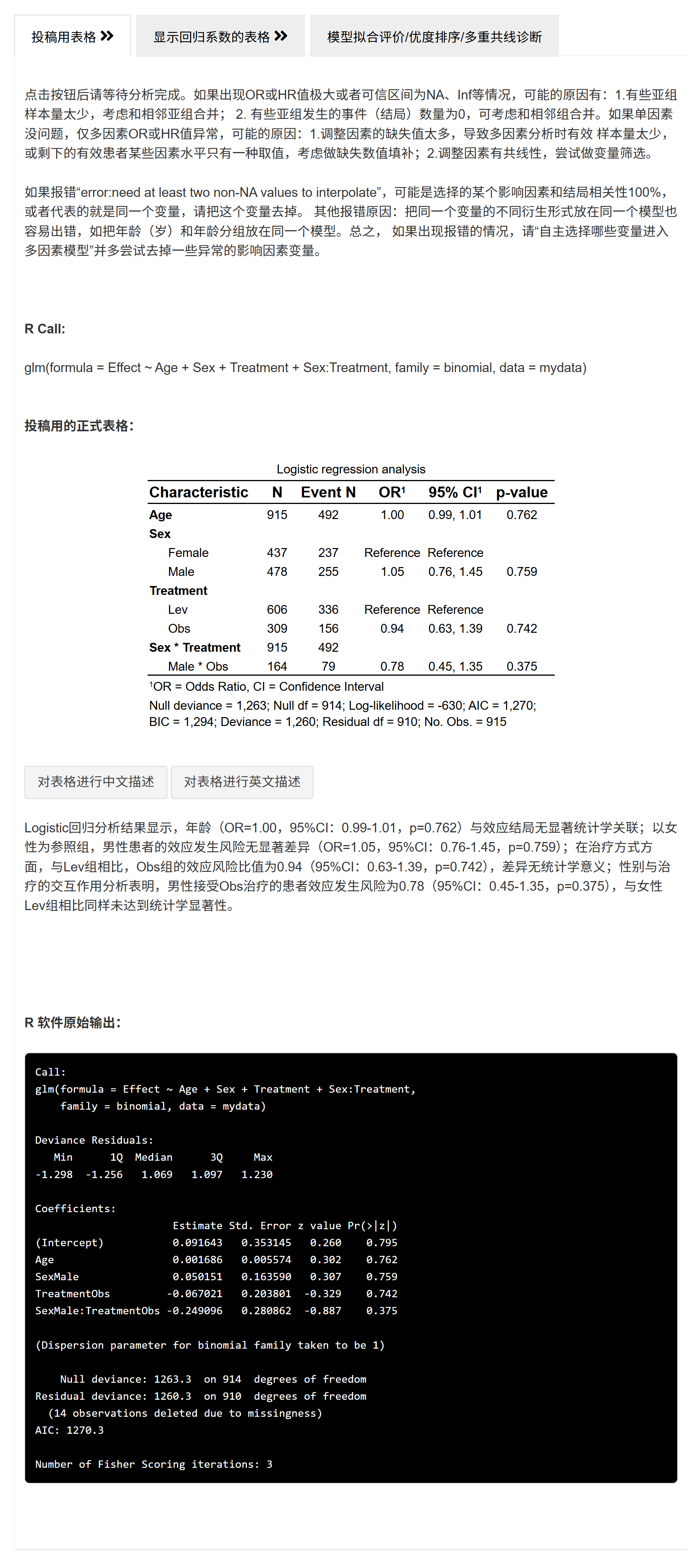
5.2 探寻可能的影响因素(增加交互作用项的多因素分析)
5.2.1 什么是交互作用(Interaction / Effect Modification)?
当自变量 A 对结局的影响取决于另一变量 B 的取值时,A 与 B 之间存在交互作用。统计建模里通常用乘积项(例如 A*B 或 A:B)表示。在不同模型中,这个“依赖关系”是在不同刻度上体现的:
线性回归:在原始数值刻度上(加法刻度)体现。
Logistic / Poisson 回归:在 log(OR)/log(IRR) 的对数刻度上体现(乘法刻度)。
Cox 回归:在 log(HR) 的对数刻度上体现。
5.2.2 与混杂(confounding)的区别:
混杂是“第三个变量同时影响自变量与结局,导致关联被扭曲”,需要控制;
交互作用是“某变量改变了另一变量的效应大小”,需要显式建模并报告分层或条件效应。
5.2.4 医学示例:
肿瘤学:治疗 × 基因型 靶向药对 EGFR 突变阳性患者显著有效,但对阴性患者无明显获益。模型里可加入 treatment × EGFR,在 Cox 回归(HR)或 Logistic 回归(OR)上检验交互。
心血管:治疗 × 年龄 一种抗血小板药物对年轻患者降低再梗死风险更明显,而对高龄患者效果减弱。用 age × treatment 检验是否存在年龄相关的效应差异。
呼吸:吸烟 × 粉尘暴露 工业粉尘对慢阻肺发病的影响在吸烟者中更强(IRR 更高),在不吸烟者中相对较弱。用 Poisson(或负二项)回归设置 dust × smoking 检验交互。
代谢:运动干预 × BMI(连续变量) 运动干预对血糖(线性回归中的 β)下降幅度,随 BMI 增加而更明显。将 BMI(建议先中心化/标准化)与 intervention 做乘积项 BMI × intervention。
5.2.5 建模与解读要点
务必包含主效应: 建议将参与交互的每个变量的主效应(如 A、B)与交互项(A:B)一并纳入模型。
连续变量先做尺度处理更稳健: 对参与交互的连续自变量,建议中心化或标准化后再与其他变量相乘,可提升数值稳定性、降低多重共线性。
功效与事件数: 交互项会显著增加参数个数。遵循 EPV(events per variable)经验法则,确保样本量/事件数足够。
报告方式: 若交互显著(常用 P_interaction < 0.05 作为线索),需给出分层/条件效应(例如分别给出男性与女性的 OR/HR,或在不同 BMI 水平的效应曲线),并辅以森林图/分层曲线帮助阅读。
避免冗余与共线性: 避免一个变量与它的派生变量(如 age 与 age_group)同时放入同一模型;必要时对高基数分类变量合并水平。
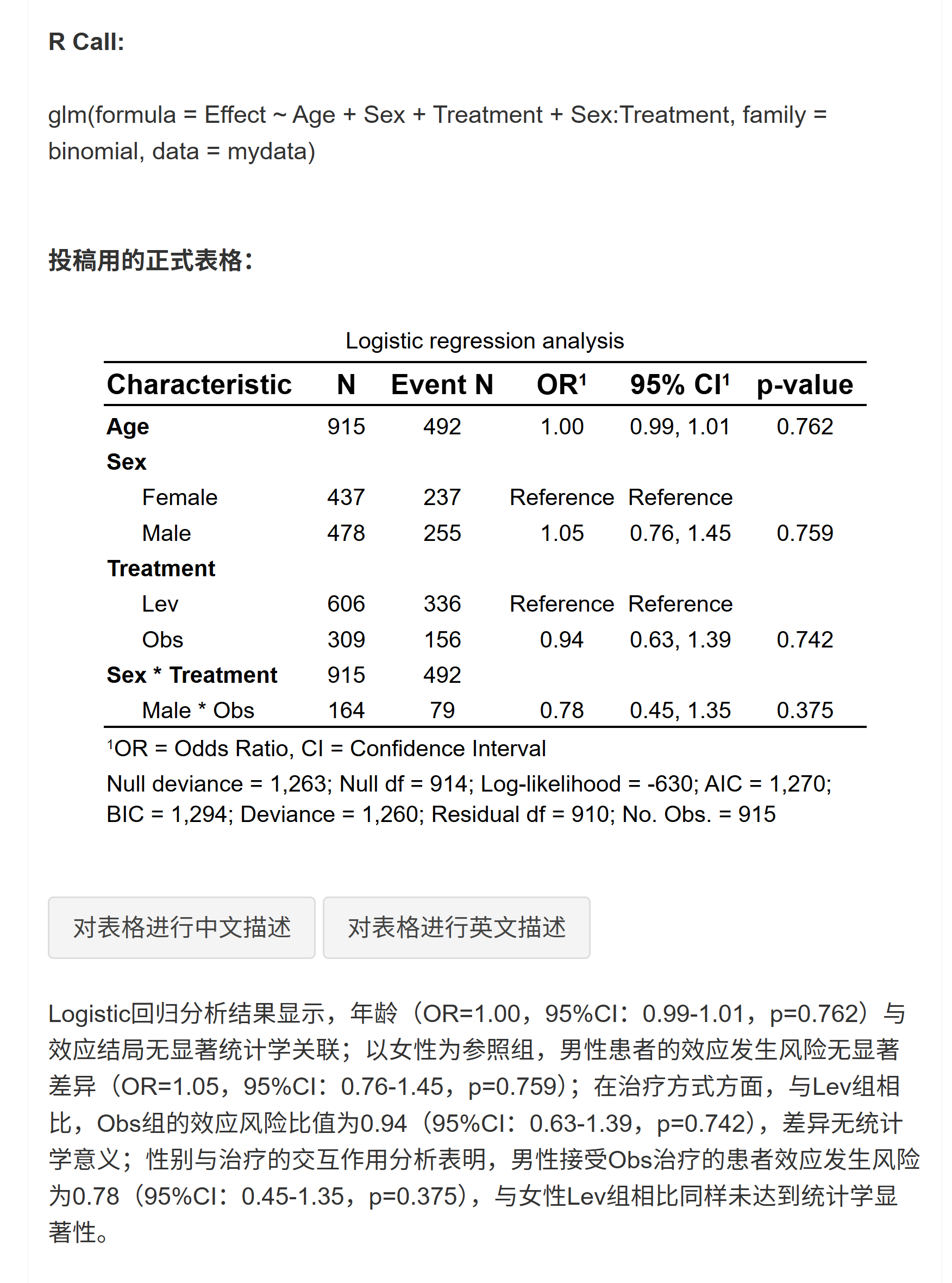
5.2.7 主要功能
多种回归模型支持:线性回归、Logistic 回归、有序 Logistic 回归、无序分类多项式回归,Cox 回归、Poisson 回归等
交互作用分析:支持多变量交互作用项的灵活添加
分类变量参照组设置:可自定义分类变量的参照组
连续变量标准化:支持中心化、标准化、Log 变换等处理
结果可视化与导出:生成标准化统计表格,支持 Word 报告导出
R 代码生成:自动生成可复现的 R 代码
5.2.8 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量:
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的 effect(疗效)为二分类变量(Good,Bad)
有序分类结局变量
如本例中的 differ 为有序分类变量(Poor, Moderate, Well)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
5.2.10 模型选择
在 “选择结局变量的类型及相应的模型种类” 部分,用户可选择不同的回归模型:
| 模型类型 | 适用场景 | R 函数 |
|---|---|---|
| 线性回归 | 连续型结局变量(如 BMI、血压等) | glm(family = gaussian) |
| Logistic 回归 | 二分类结局变量(如 有效/无效、阳性/阴性) | glm(family = binomial) |
| Log-Binomial 回归 | 二分类结局变量(如 有效/无效、阳性/阴性) | glm(family = binomial(link="log")) |
| 有序 多分类 Logistic 回归 | 有序多分类结局变量(如 轻度/中度/重度) | ordinal::clm() |
| 无序多分类 Logistic 回归 | 无序多分类结局变量(如 肿瘤分型、职业类别) | nnet::multinom() |
| Cox 回归 | 生存数据(如 OS、PFS) | survival::coxph() |
| Poisson 回归 | 计数型结局变量(如 发作次数、细胞计数) | glm(family = poisson) |
| Poisson + offset | 比例型结局变量(如 受精率、有效率) | glm(family = poisson, offset = log(...)) |

5.2.12 交互作用分析(重点)
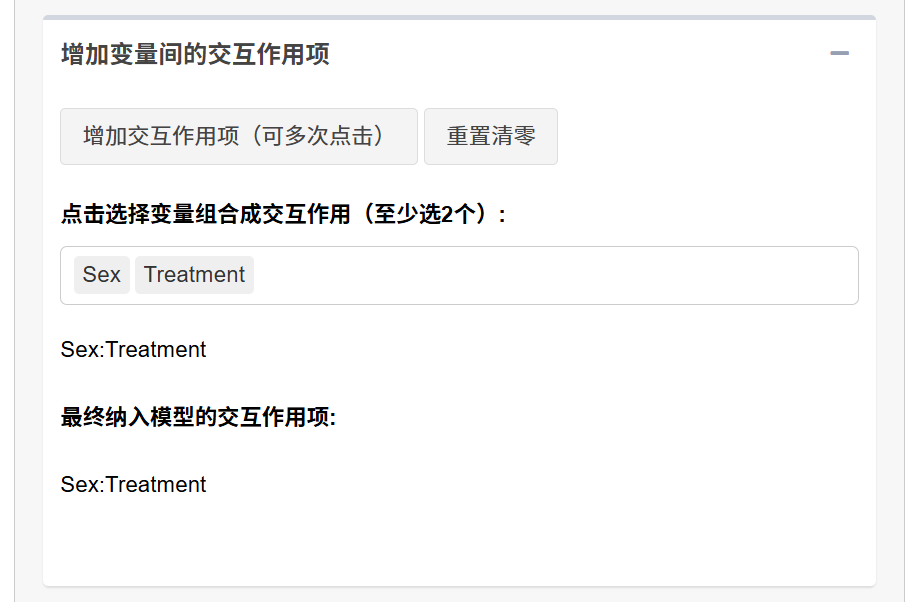
5.2.12.1 如何添加交互作用项
点击 “增加交互作用项” 按钮,可多次点击,每点击一次,添加一项新的交互作用
在每个选择器中勾选 2 个或更多变量(如
age和sex)系统自动生成交互作用公式(如
age:sex)
5.2.14 连续变量标准化
支持 中心化(centered)、标准化(standardized) 和 Log 变换
适用于:
消除量纲影响(如 BMI 和年龄的单位不同)
改善模型收敛性
5.2.17 结果输出
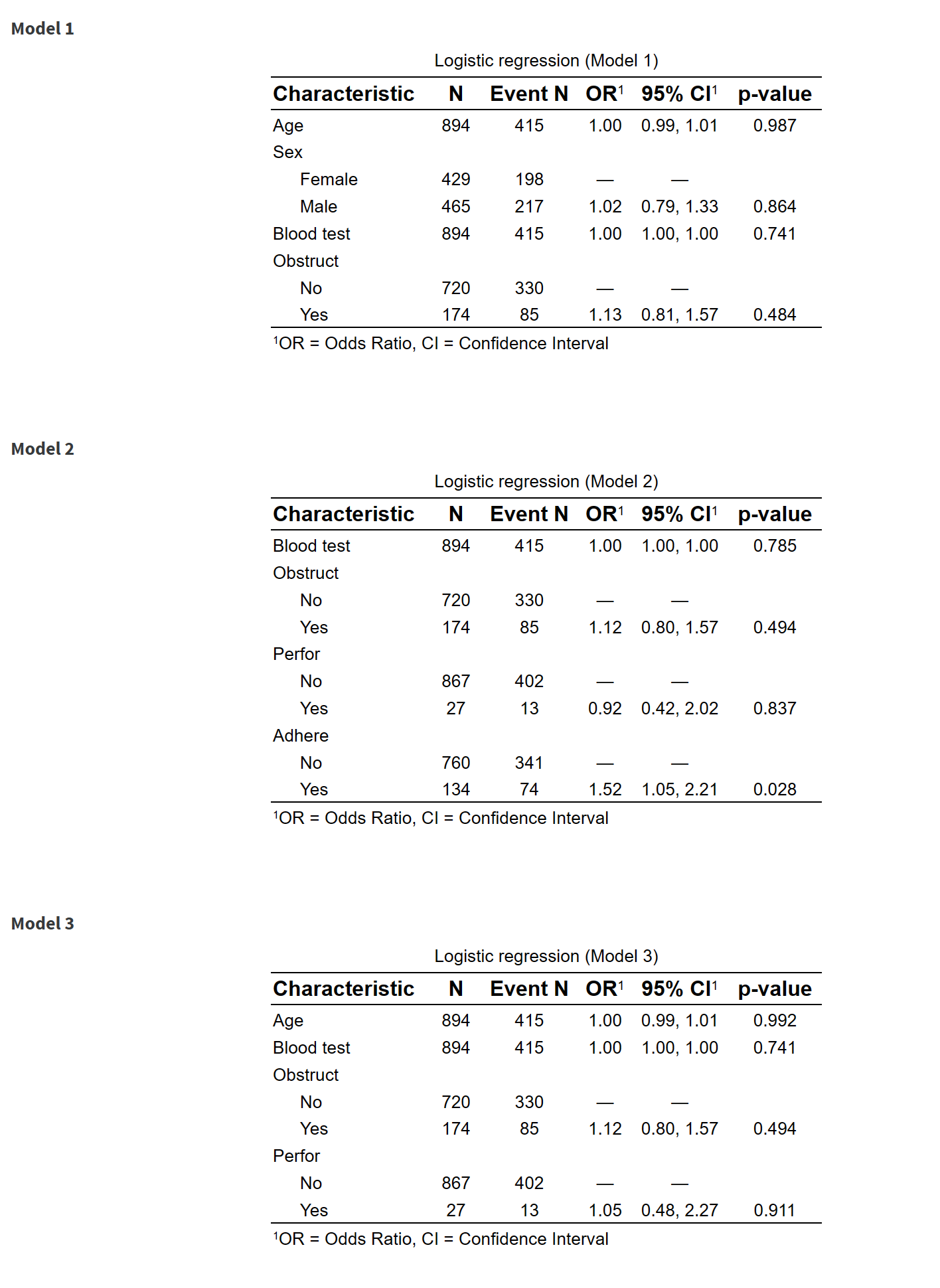
5.3 根据多因素不同自变量组合的多模型批量比较及拟合优度评价
5.3.3 引言
在医学统计分析中,我们经常要评估各种因素如何影响某个特定的健康结局。这些因素可以是生活习惯(如抽烟、饮酒)、遗传倾向、疾病状态(如心脏病)、环境暴露或者医疗干预(如药物治疗)。为了理解这些影响因素(或自变量)与健康结局(或因变量)之间的关系,研究者会运用多种统计回归模型来分析数据。
回归分析是一种强大的统计工具,它可以揭示一个或多个自变量对一个因变量的影响。根据因变量的类型和研究的需求,可以选择不同类型的回归分析:
逻辑回归(Logistic regression)适用于二分类结果变量,如疾病有无。
线性回归(Linear regression)适合连续结果变量,如血压或胆固醇水平。
Cox回归(Cox proportional hazards regression)用于分析生存时间数据,即时间到一个事件(如死亡或复发)的发生。
Poisson 回归 适用于计数数据或事件发生率的分析。
在医学研究中,多因素回归模型是一种常用的统计方法,用来评估多个自变量(即独立变量)如何同时影响一个因变量(即依赖变量)。拟合多个模型的目的是为了寻找解释因变量变化的最佳自变量组合。通过比较不同模型的拟合优度,研究者可以评估哪个模型最能准确描述数据。同时,分析模型的共线性可以发现自变量之间是否存在高度相关的问题,这可能会影响模型的稳定性和解释性。
例如研究心血管疾病的风险因素。研究者可能会建立一个多因素回归模型,将年龄、性别、血压、胆固醇水平、吸烟状态等自变量纳入模型,来探索心血管疾病事件(心脏病发作、中风等)的独立影响因素。通过构建不同的模型组合,比如一个模型只包括年龄和性别,另一个模型加入了血压和胆固醇水平,研究者可以判断哪些因素是心血管疾病的独立影响因子,以及它们的相对重要性。
5.3.4 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.3.5 操作步骤
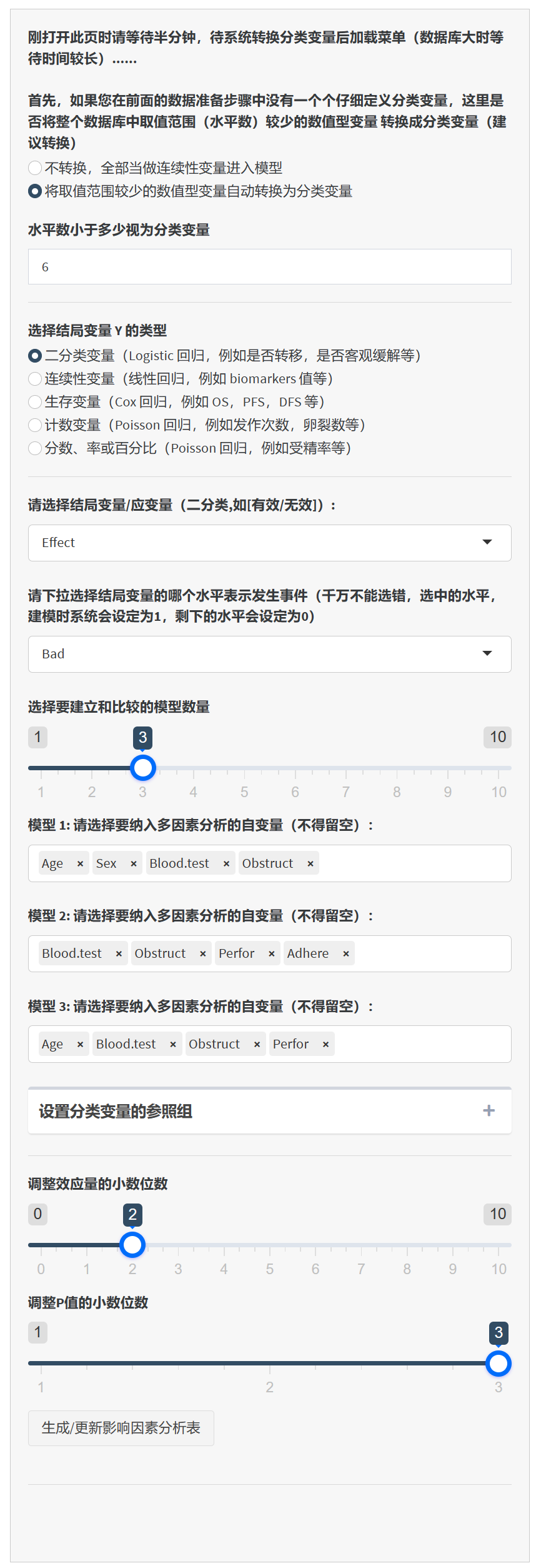
步骤 1: 数据准备
- 在开始之前,请确保您已经在软件的“数据准备”页面上传了您的数据集,并在“定义字段”选项卡检查并应用了更改。
步骤 2: 等待数据转换
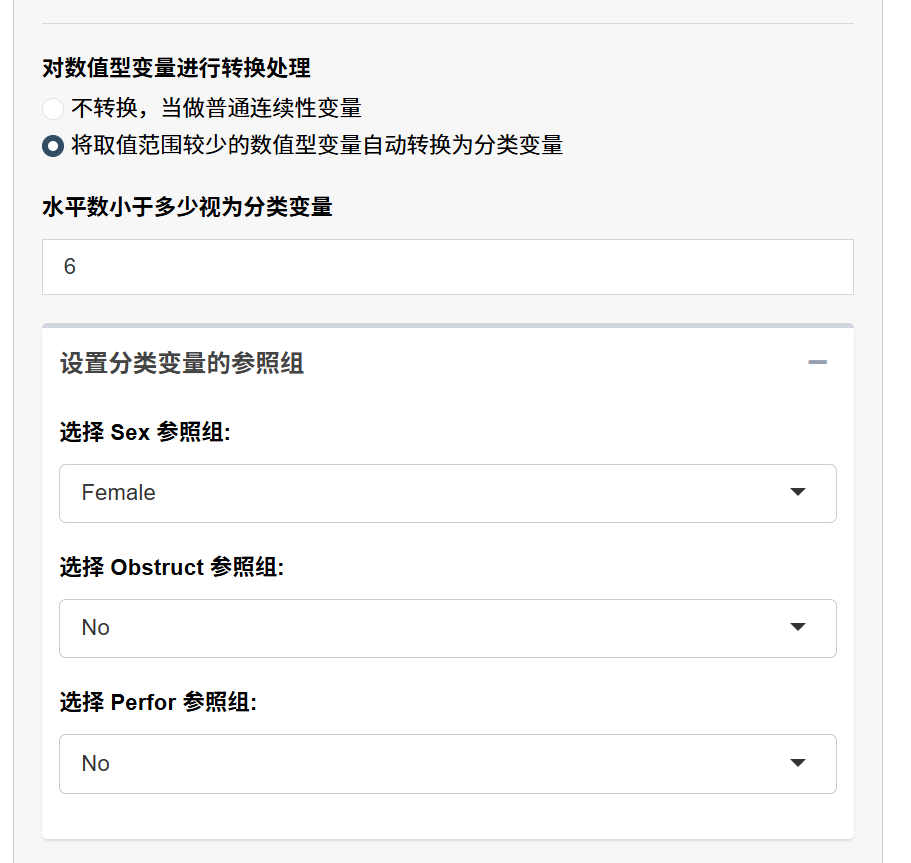
- 打开页面后,请耐心等待半分钟让系统处理并加载您的数据。如果您的数据库较大,这个过程可能需要更长时间。系统会自动把水平数低于6的数值型变量转换为分类变量,当然您也可以手动改回来不做转换
步骤 3: 选择模型类型
- 接下来,您需要根据结局变量的类型选择合适的模型。可选的模型包括二分类变量(Logistic回归)、连续性变量(线性回归)、生存变量(Cox回归)、计数变量(Poisson回归)等。
步骤 4: 选择结局变量
- 根据您选择的模型类型,系统会要求您从数据库中选择相应的结局变量。例如,如果您选择了Logistic回归,就需要选择一个二分类的结局变量。
步骤 5: 定义模型自变量
- 确定您想要在模型中放入哪些自变量。
步骤 6: 模型比较
- 您可以建立并比较多个模型。选择要比较的模型数量,并为每个模型选择要放入的自变量。请确保不同模型之间的自变量选择不完全相同。
步骤 7: 分类变量参照组设定
- 对于非数值型的分类变量,您需要为每个变量选择一个参照组。
步骤 8: 结果呈现
- 确定您如何呈现结果数据,包括是否显示N和Event值,以及效应量和P值的小数位数。
步骤 9: 生成结果
- 完成上述设置后,点击相应的按钮生成影响因素分析表。
在整个过程中,如果您在某个步骤遇到了问题,系统可能会提供警告或错误信息。请按照提示进行相应的修改。如果一切顺利,您将能够生成反映不同影响因素对结果影响的统计模型比较表格。
5.4 探寻可能的影响因素(混合效应模型,多水平模型,Mixed model)
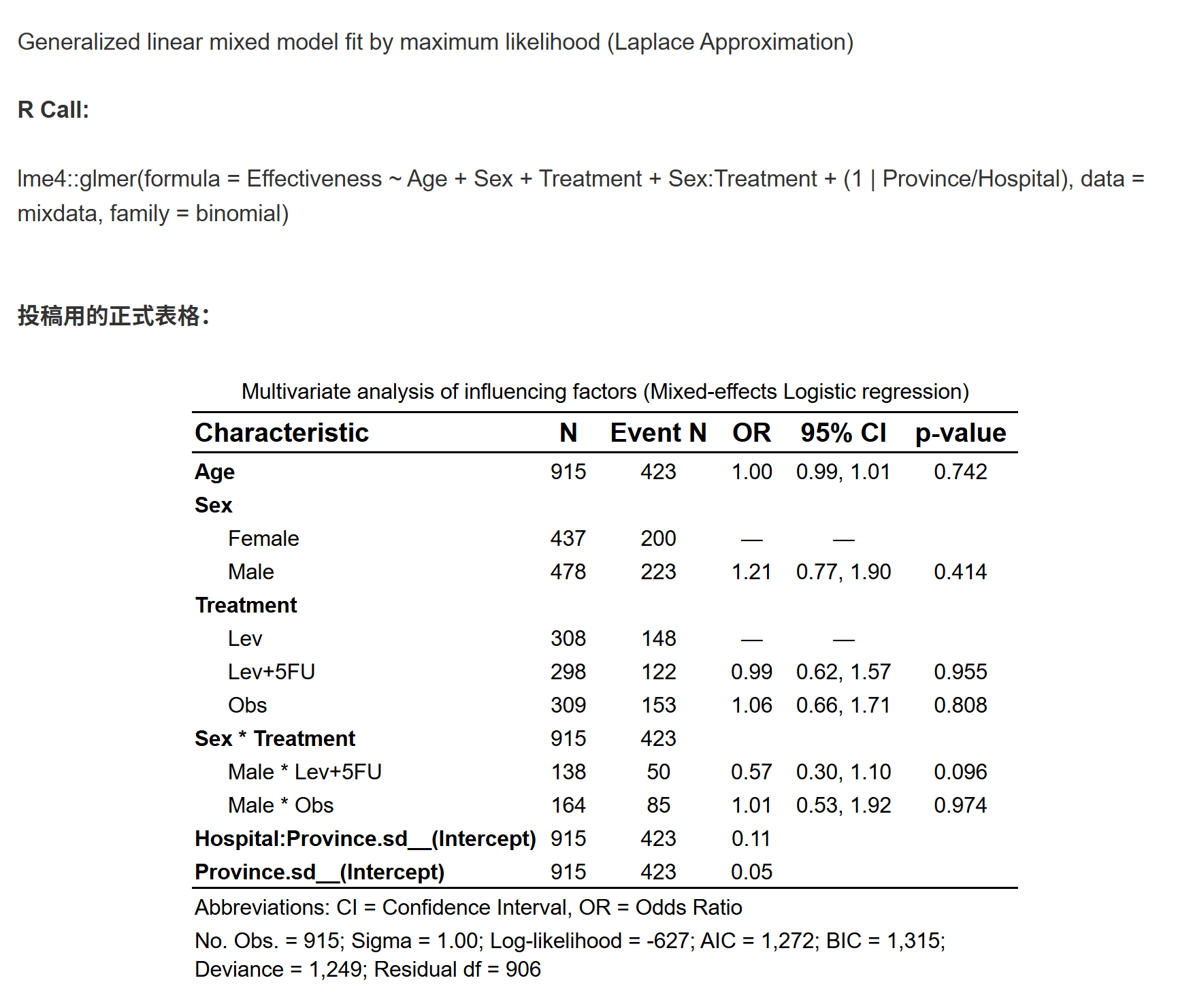
混合效应模型是一类非常重要的统计模型,它广泛应用于各种科学研究领域。混合效应模型是线性模型的推广,它引入了固定效应和随机效应。固定效应通常是我们主要关注并且在所有个体或样本中都相同或者类似的因素,如年龄、性别等。固定效应参数是常数,不随个体或样本的不同而变化。
相反,随机效应则是指影响结果的因素在不同的个体或样本之间具有差异性,这种差异性通常是随机的,无法用固定的数值来描述。随机效应在个体或样本之间是变化的,并且通常假设服从正态分布。
医学中混和效应模型常见的场景有:多水平模型和重复测量模型
1) 多水平模型主要是患者之间有地区聚集性,导致个体之间并不独立,例如多中心研究中,每个中心的患者的环境有相似性,每个不同医生治疗的患者也有相似性。
举例:
在医学研究中,比如我们想研究心脏病的发病率与吸烟、年龄、性别等因素的关系。这些吸烟、年龄、性别就是固定效应,因为我们假设这些因素的效应是在所有个体之间都保持不变的。
然而,如果我们的数据来自不同的医院或者不同的城市,我们可能会考虑到医院或者城市对疾病发生率的影响。这种影响可能是由于各个医院或者城市的医疗条件、生活环境、生活习惯等多种因素造成的。这时,医院和城市就可以被看作是随机效应。我们无法具体衡量每个医院或者城市对疾病发生率的具体影响,但是我们可以假设这种影响在各个医院或者城市之间是存在差异的,并且这种差异是随机的。
因此,通过引入随机效应,混合效应模型可以更好地拟合这种数据,并且可以更准确地估计固定效应(如吸烟、年龄、性别)对疾病发生率的影响。
混合效应模型可以用于更加复杂的场景,例如研究对象之间存在群体差异(如不同医院的病人、不同地区的居民等)或者观测数据存在时间序列关系(如对同一病人多次进行的观测)等情况。
例如,在医学研究中,我们可能关注某种疾病的发生率是否与特定的风险因素有关,同时考虑到各个医院的影响。此时,我们的因变量是二项分布(患病与否),自变量是风险因素(如年龄、性别、吸烟与否等),随机效应可以是医院(即不同医院可能会对疾病的发生率产生不同的影响)。通过混合效应模型,我们可以有效地建立因变量、自变量和随机效应之间的关系,从而更准确地探索特定风险因素对疾病发生的影响。
2) 重复测量模型
在医学研究中,混合效应模型通过引入固定效应和随机效应,可以有效处理多次重复测量数据,例如在一年内每月对一组糖尿病患者的血糖水平进行监测。
固定效应是我们关心的、并且在所有个体或样本中都相同或类似的因素,如饮食控制和运动治疗。这些因素是我们想要研究其对血糖水平影响的主要变量。
然而,每个患者的血糖水平并不是只受固定效应影响,他们的基线健康状况、生活习惯、遗传背景等个体特性也会对血糖水平产生影响。同一患者在不同时间的血糖水平测量值之间往往存在一定的相关性,即他们具有聚集性,这是由于他们受到同一个个体特定特性的影响。这种在个体间的测量值的聚集性或相关性,可以通过引入随机效应来进行建模。
具体来说,我们可以假设每个患者都有自己的随机效应,这个效应对该患者所有的测量值都有影响。引入随机效应后,我们就可以在模型中同时考虑到个体间的差异(即随机效应)和治疗效应(即固定效应)。
因此,混合效应模型可以更好地处理这种重复测量数据,可以更准确地估计固定效应对血糖水平的平均影响,并且可以更好地预测每个患者在未来的血糖变化趋势。这在医学研究中具有重要的应用价值,对于疾病的治疗和预防提供了重要的参考依据。
本软件提供了混合效应模型模块,可以用于估计具有类别和/或连续因变量和自变量的混合效应模型,还提供了各种选项来方便用户估计交互作用、简单斜率、简单效应等。
本软件可以估计多种线性模型,包括固定效应和随机效应模型。公式的写法和R中lme4包相同,例如 (1|hospital) 表示将医院作为随机效应。
5.4.1 混和效应模型分析
本模块专门用于进行混合效应模型(Mixed Effects Models)的影响因素(多因素)分析。混合效应模型是一种同时包含固定效应和随机效应的统计模型,适用于处理具有层级结构或重复测量的数据。
5.4.2 主要功能
支持多种类型的混合效应模型:线性混合模型、Logistic混合模型、Poisson混合模型、有序Logistic混合模型和Cox混合模型
提供交互式操作界面,无需编程即可完成复杂分析
自动生成符合学术规范的统计表格
支持多种数据预处理选项
一键生成可下载的Word格式分析报告
5.4.3 数据准备
在使用本软件前,请确保您的数据已经完成以下准备工作:
数据已经导入到系统中
变量类型已正确设置(连续变量设为numeric,分类变量设为factor)
有序分类变量已按从低到高顺序排列
数据中不包含异常值或错误值
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
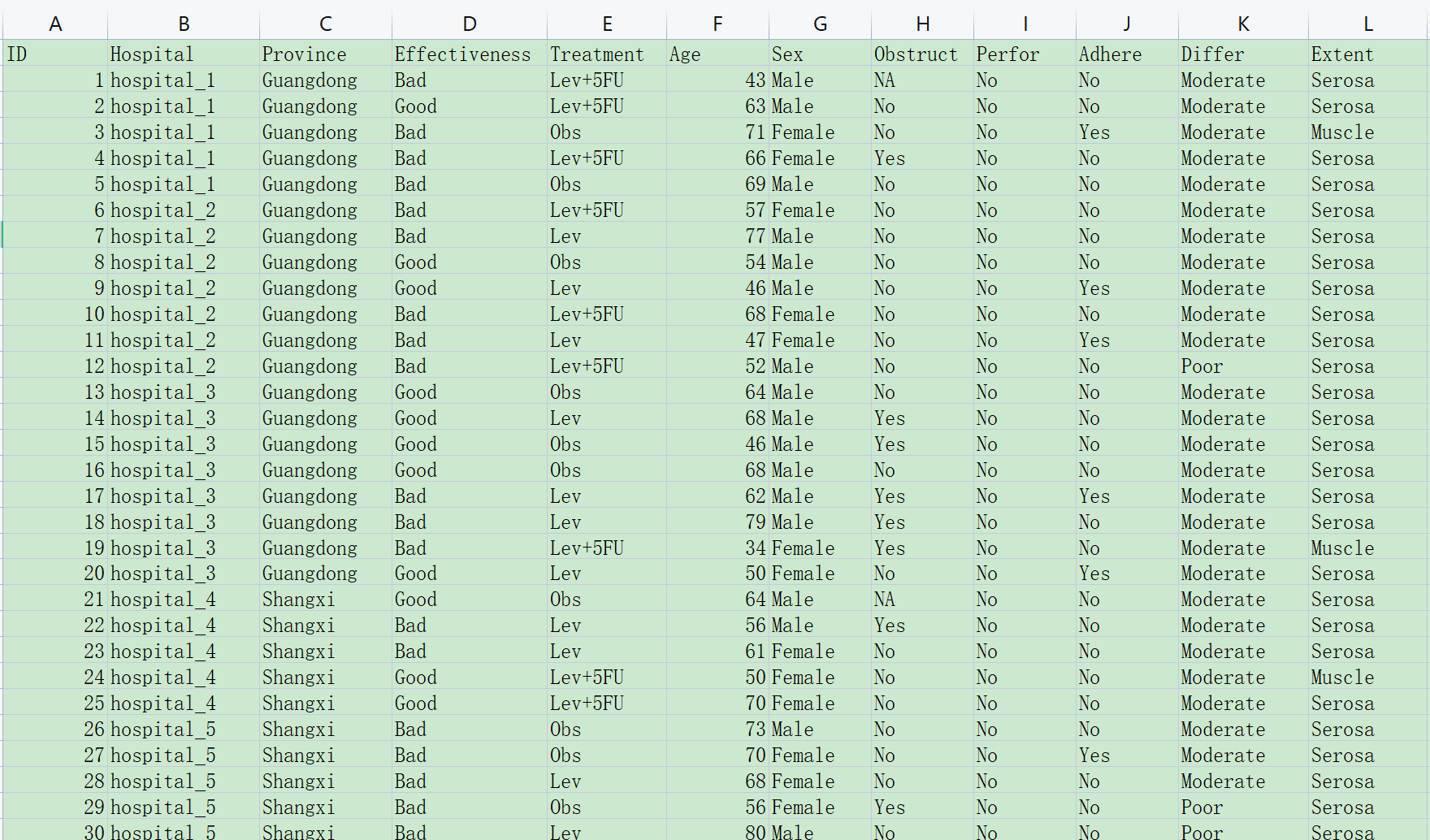
本样例数据的特点:
表示群组(聚集)的变量,如 Hospital,Province
代表结局的应变量:例如上图中的Effectiveness,是一个二分类变量,代表疗效。
解释变量(自变量):例如上图中的Age、Sex、Treatment等等一系列指标,应当设置成固定效应
5.4.4 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“探寻可能的影响因素(多因素分析),所有因素分析结果列入表格(混合效应模型,多水平模型,Mixed model)” 进入模块:
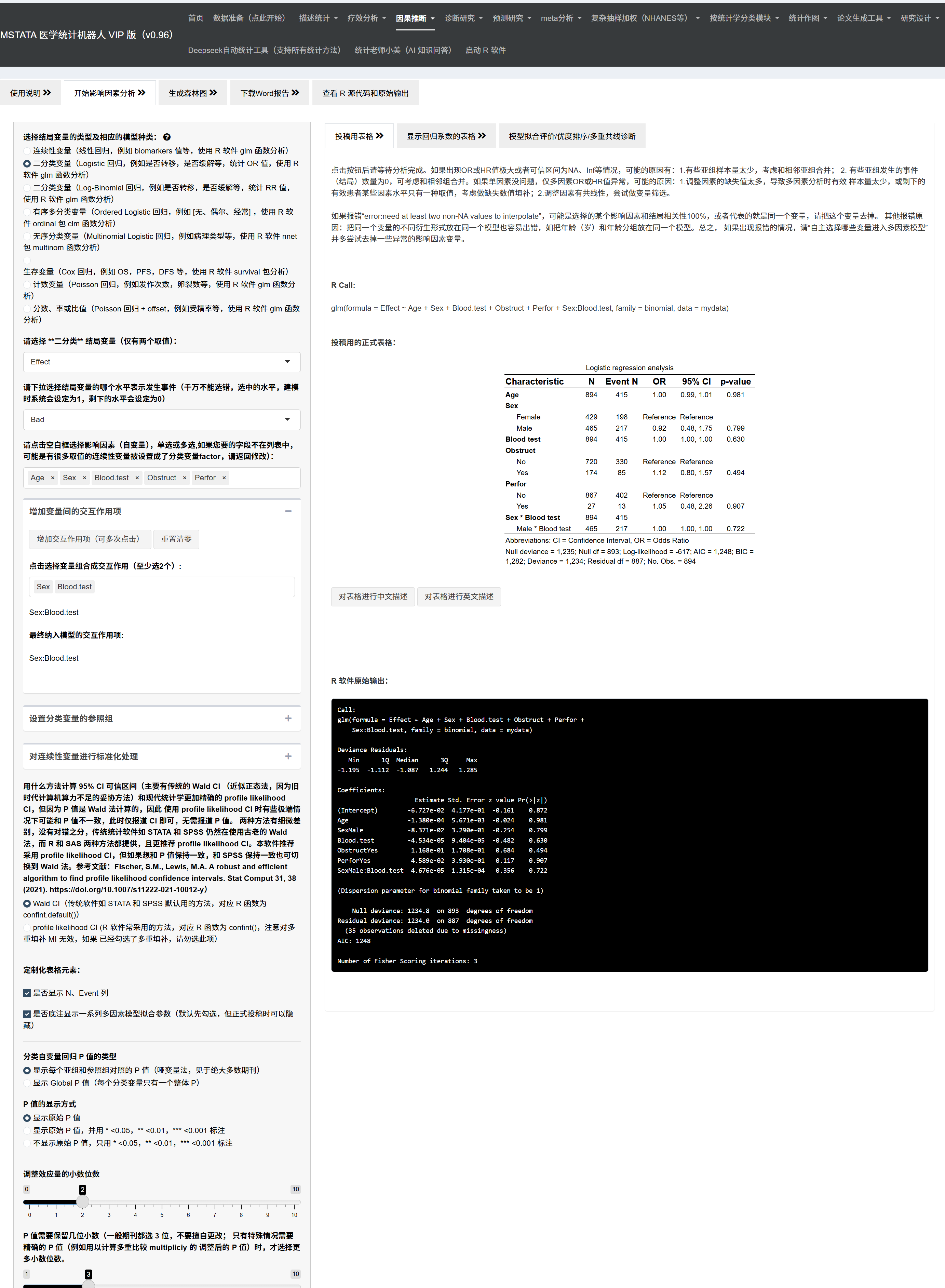
5.4.5 模型选择
选择模型类型:
根据您的因变量类型,从下拉菜单中选择合适的模型:
连续性变量:选择”线性混合效应模型”(如生物标志物等)
二分类变量:选择”Logistic混合效应模型”(统计OR值)或”Poisson混合效应模型”(统计RR值)
有序多分类变量:选择”有序Logistic混合效应模型”
生存变量:选择”Cox混合效应模型”(如OS、PFS等)
计数变量:选择”Poisson混合效应模型”
分数、率或比值:选择”Poisson混合效应模型+offset”

选择因变量:
根据所选模型类型,系统会自动筛选出符合条件的变量供您选择
点击下拉菜单选择您的因变量
5.4.6 特殊设置(根据模型类型)
5.4.7 选择自变量(固定效应)
选择固定效应变量:
从变量列表中选择您想研究的自变量
可以多选,系统会自动排除与因变量高度相关的变量
添加交互作用项(可选):
点击”增加交互作用项”按钮
从弹出的菜单中选择至少2个变量组合成交互项
可以多次点击添加多个交互项
点击”重置清零”可以清除所有交互项
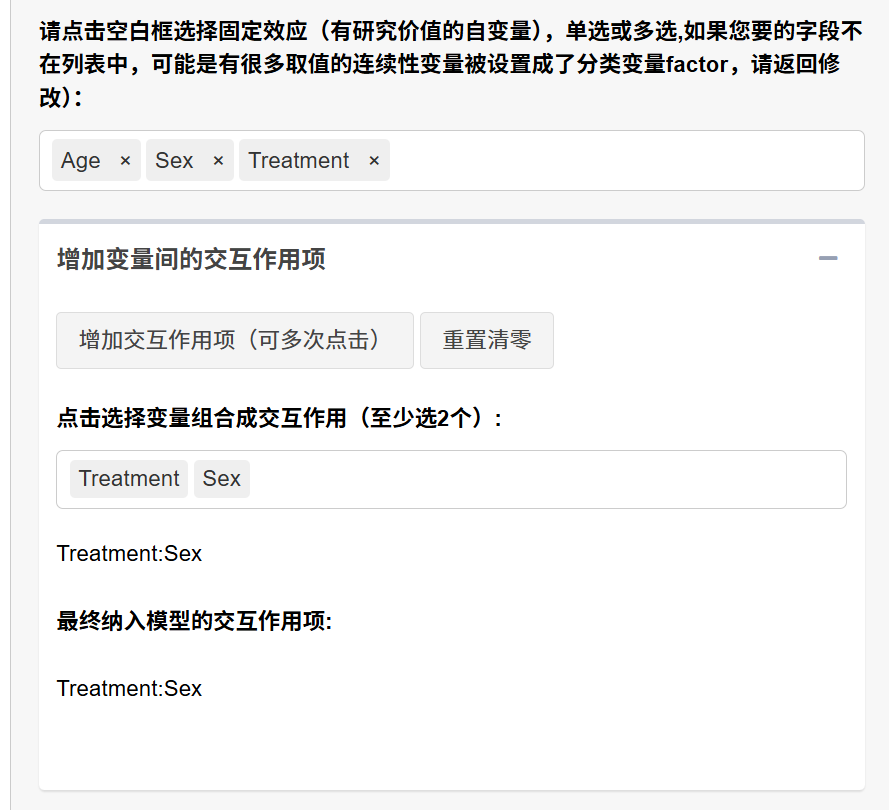
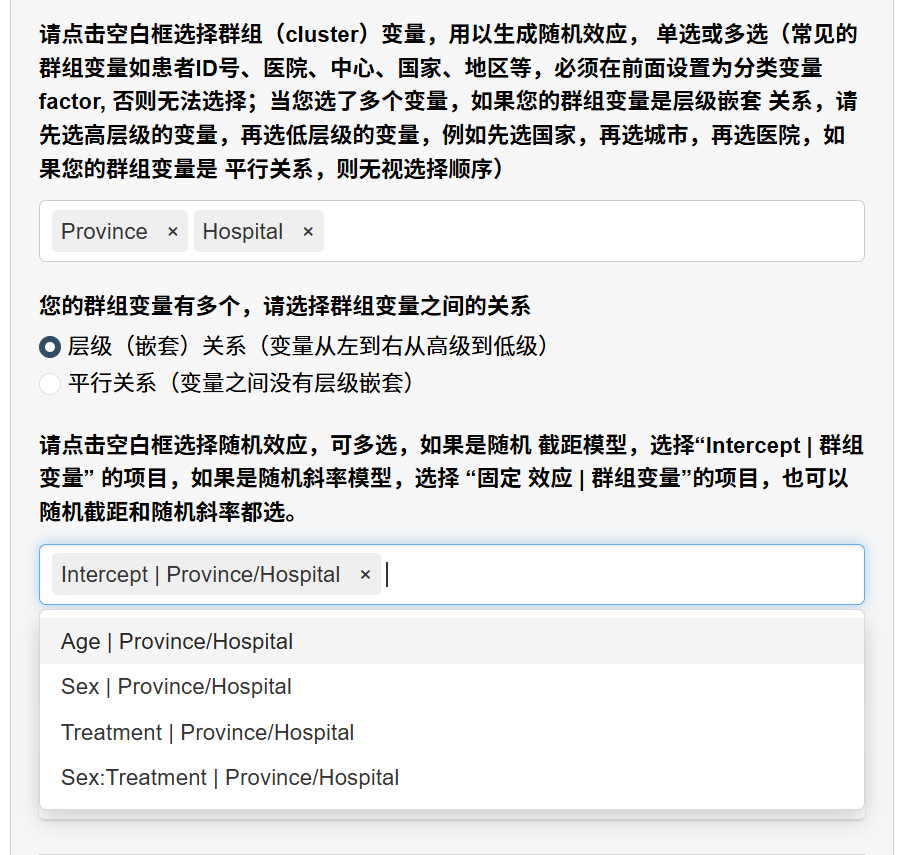
5.4.8 设置随机效应
选择群组变量:
选择用于生成随机效应的群组变量(如患者ID、医院、中心等)
可以多选,系统最多支持4个群组变量
指定群组关系(当选择多个群组变量时):
如果是层级嵌套关系(如国家→城市→医院),选择”层级(嵌套)关系”
如果是平行关系(如医院和医生),选择”平行关系”
选择随机效应项:
系统会根据您选择的群组变量自动生成可能的随机效应组合
选择您需要的随机效应:
随机截距模型:选择”Intercept | 群组变量”
随机斜率模型:选择”固定效应 | 群组变量”
可以同时选择随机截距和随机斜率
5.4.9 模型参数设置
设置分类变量参照组:
对于每个分类自变量,从下拉菜单中选择参照组(基线组)
系统默认选择第一个水平作为参照组
连续变量标准化处理(可选):
对于每个连续变量,可以选择:
不做处理
中心化处理(减去均值)
标准化处理(中心化后除以标准差)
Log变换
表格显示选项:
选择是否显示N、Event列
选择是否显示模型拟合参数
选择P值显示方式:
原始P值
原始P值加星号标注
仅星号标注
调整效应量的小数位数
调整P值的小数位数
5.4.11 查看结果
分析完成后,系统会显示以下结果:
模型信息:
模型类型
R调用公式
主要结果表格:
固定效应估计值、置信区间和P值
随机效应方差成分
有序Logistic模型特有结果:
- 模型截距/阈值表
单因素和多因素合并表格(可选)
R原始输出:
- 完整的模型摘要信息

5.4.13 原理说明
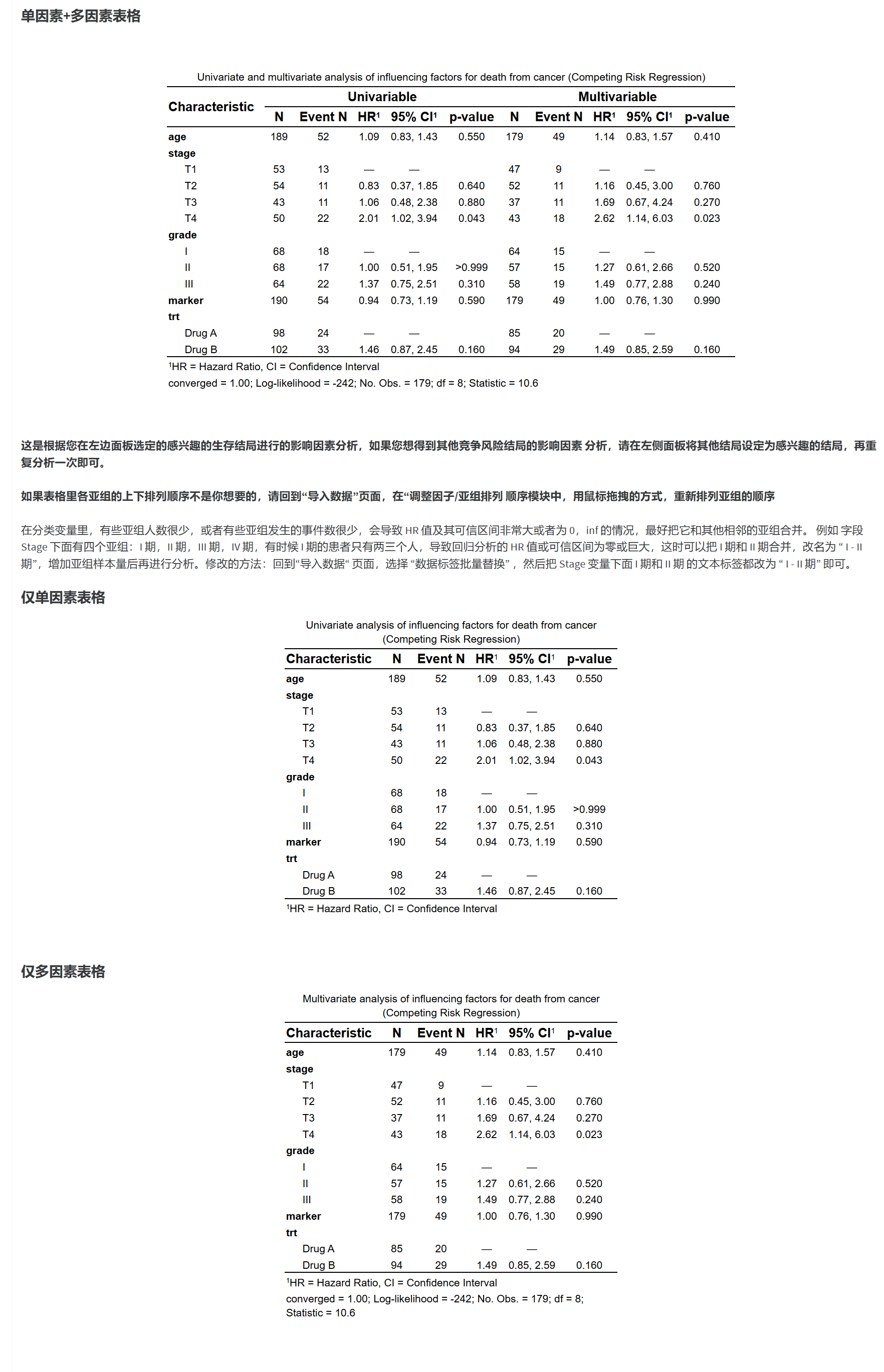
5.5 探寻可能的影响因素(竞争风险模型 Competing Risks Regression)
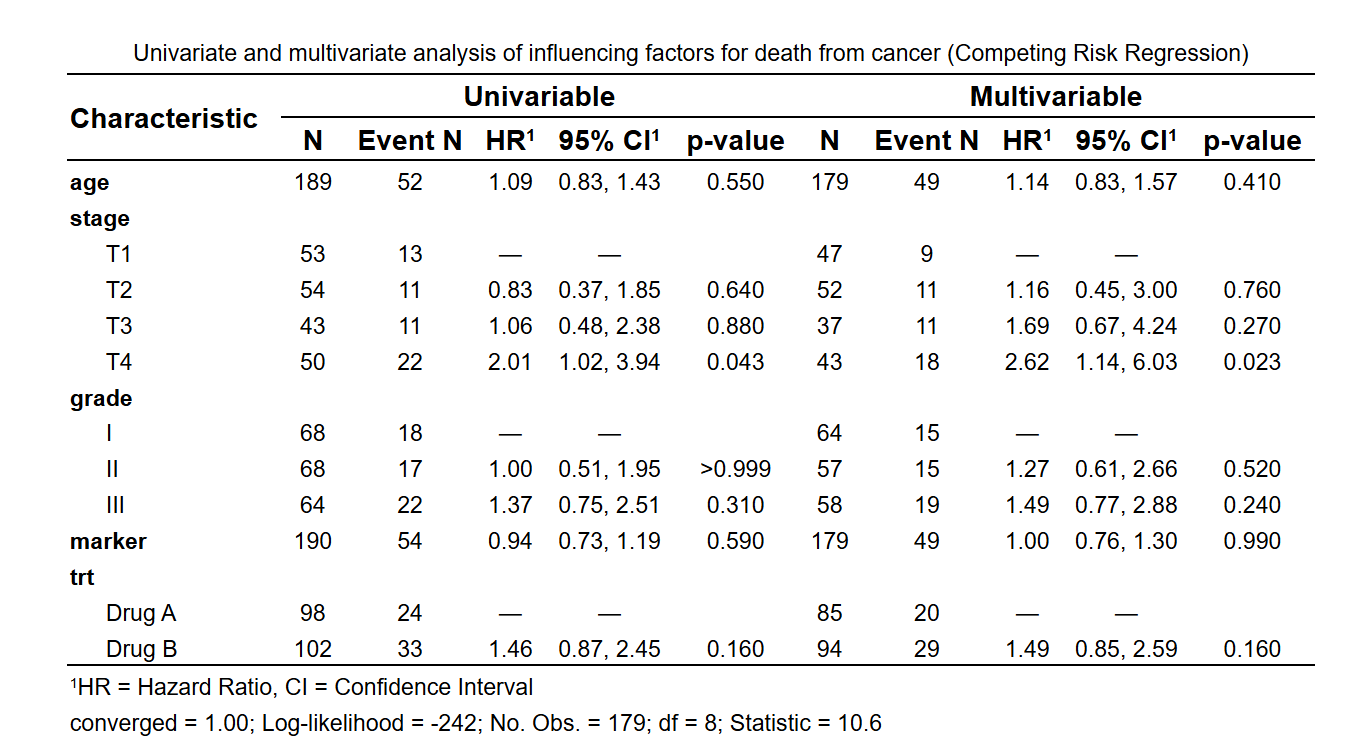
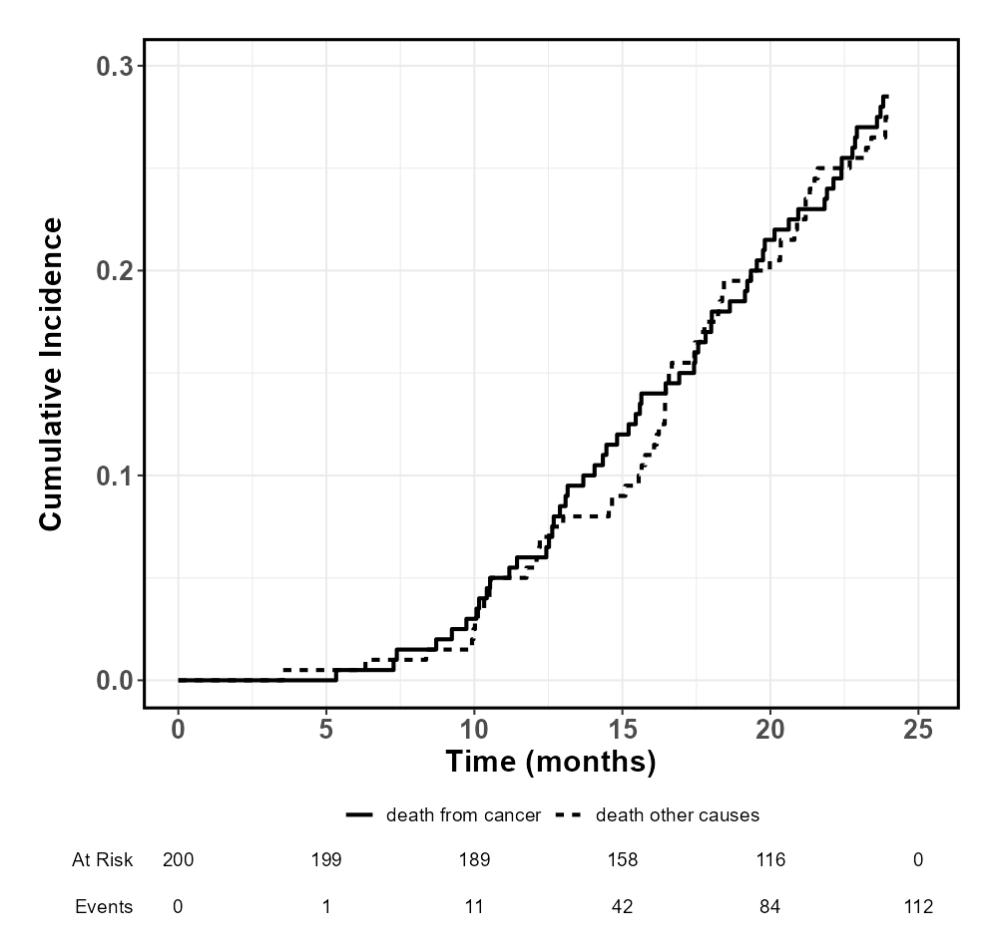
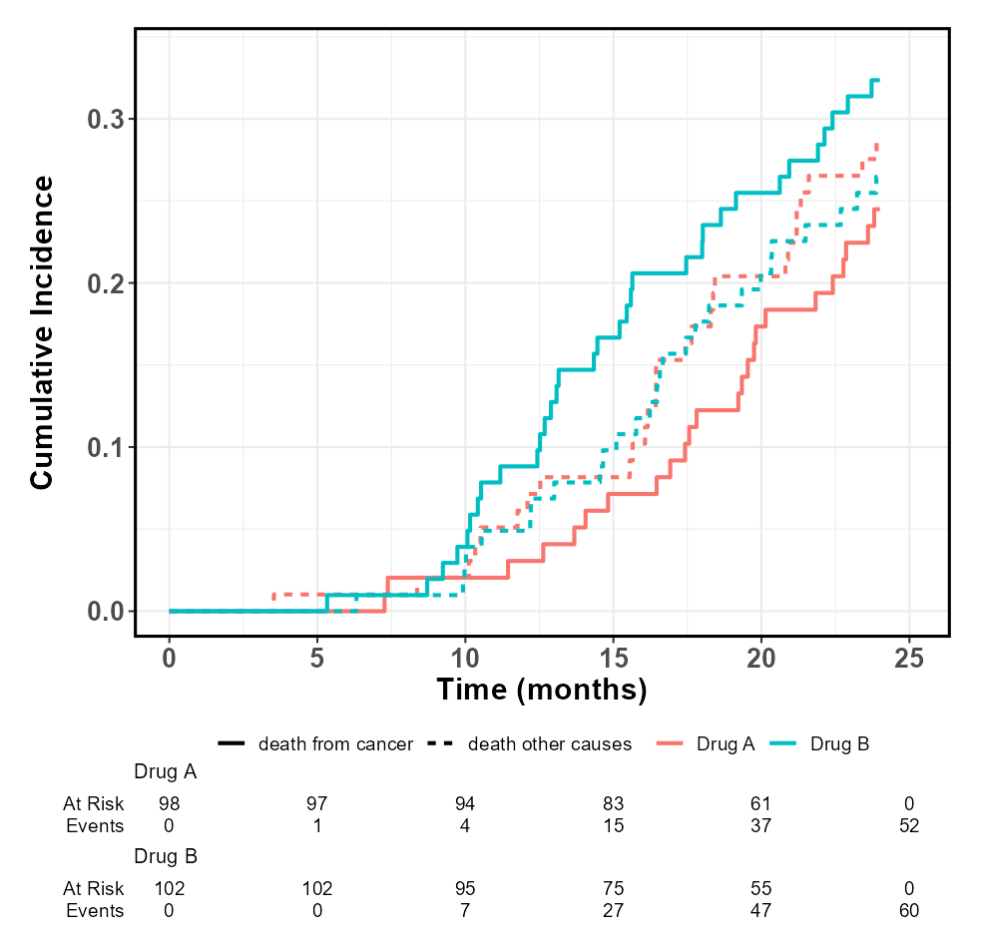
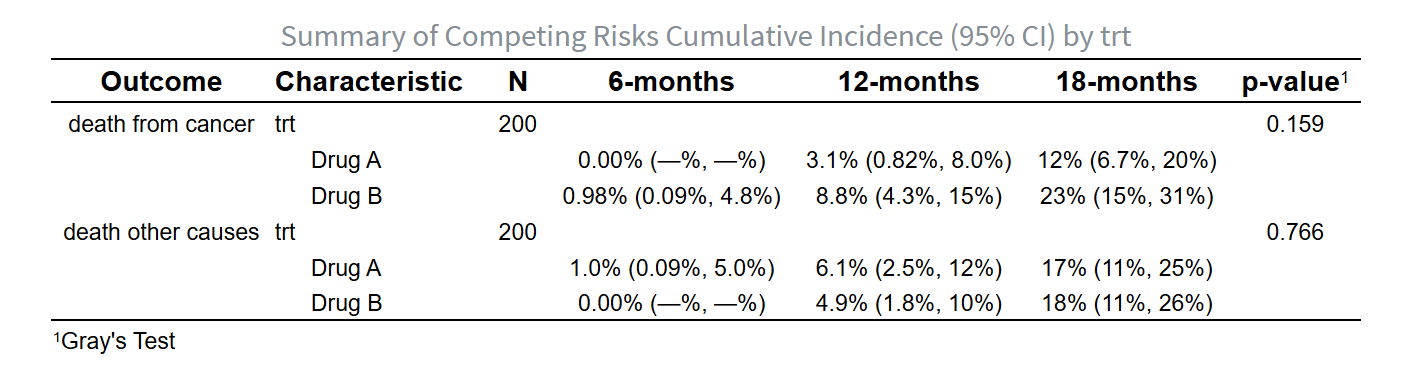
5.5.1 竞争风险模型简介
竞争风险模型是一种统计方法,用于分析多个互相排斥的事件发生时间的数据。与传统的生存分析不同,竞争风险模型考虑了一个事件的发生会影响其他事件的发生概率。在医学、流行病学和公共卫生研究中,竞争风险模型广泛应用于多种结局的分析。
5.5.2 定义与出处
竞争风险模型最早由 Gray 和 Fine & Gray 等学者提出,他们的方法论在各类统计学和生存分析的经典著作中得到了广泛讨论和应用。Gray 提出的累积发病率函数 (CIF) 及其相关的 Fine & Gray 竞争风险回归模型为这一领域奠定了基础。
5.5.4 互斥事件的概念
在竞争风险模型中,互斥事件指的是一个事件的发生会排除其他事件的发生。例如,在一项研究中,如果患者可以因不同原因死亡(如死于癌症或死于其他疾病),一旦某个患者因癌症去世,他便不可能再死于其他疾病。因此,这些结局是互斥的。竞争风险模型正是通过考虑这些互斥事件的相互排斥关系来进行分析的。
5.5.5 传统生存分析的弊端
如果在存在竞争结局的情况下仍然使用传统的生存分析方法(如Kaplan-Meier法或Cox回归模型),会存在以下弊端:
高估事件发生概率:传统生存分析会假设所有其他竞争事件不存在,这会导致对目标事件发生概率的高估。
错误的风险估计:忽略竞争事件的影响,会导致风险因子的估计值偏差,从而无法准确识别真正的危险因素。
误导的研究结论:由于未考虑竞争风险,研究结论可能会具有误导性,不利于临床决策和公共卫生政策的制定。
5.5.6 医学研究应用示例
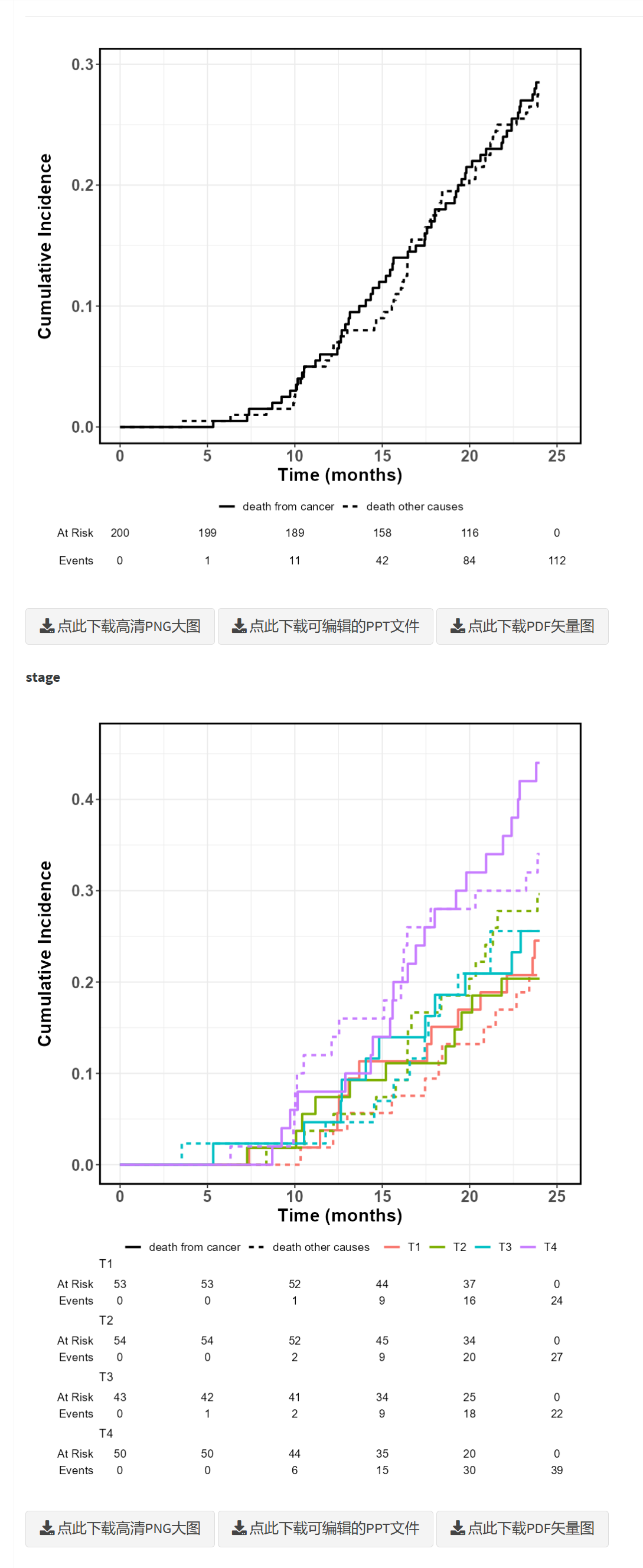
在一项关于癌症患者的研究中,研究者可能会关心患者的不同结局,如死于癌症和死于其他疾病。假设在这项研究中有一部分患者死于癌症,而另一部分患者死于其他疾病。如果仅使用传统生存分析方法,会忽略死于其他疾病的竞争风险,导致对死于癌症的概率估计过高。
通过使用竞争风险模型,研究者能够分别估计患者死于癌症和死于其他疾病的累积发病率,精确识别影响这些结局发生的危险因素。这对于临床决策制定和个体化治疗方案的选择具有重要意义。
本软件提供了便捷的工具,帮助您进行竞争风险模型的单因素和多因素分析,使您能够在复杂的数据中挖掘出有价值的信息,为您的研究提供强有力的支持。
5.5.7 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
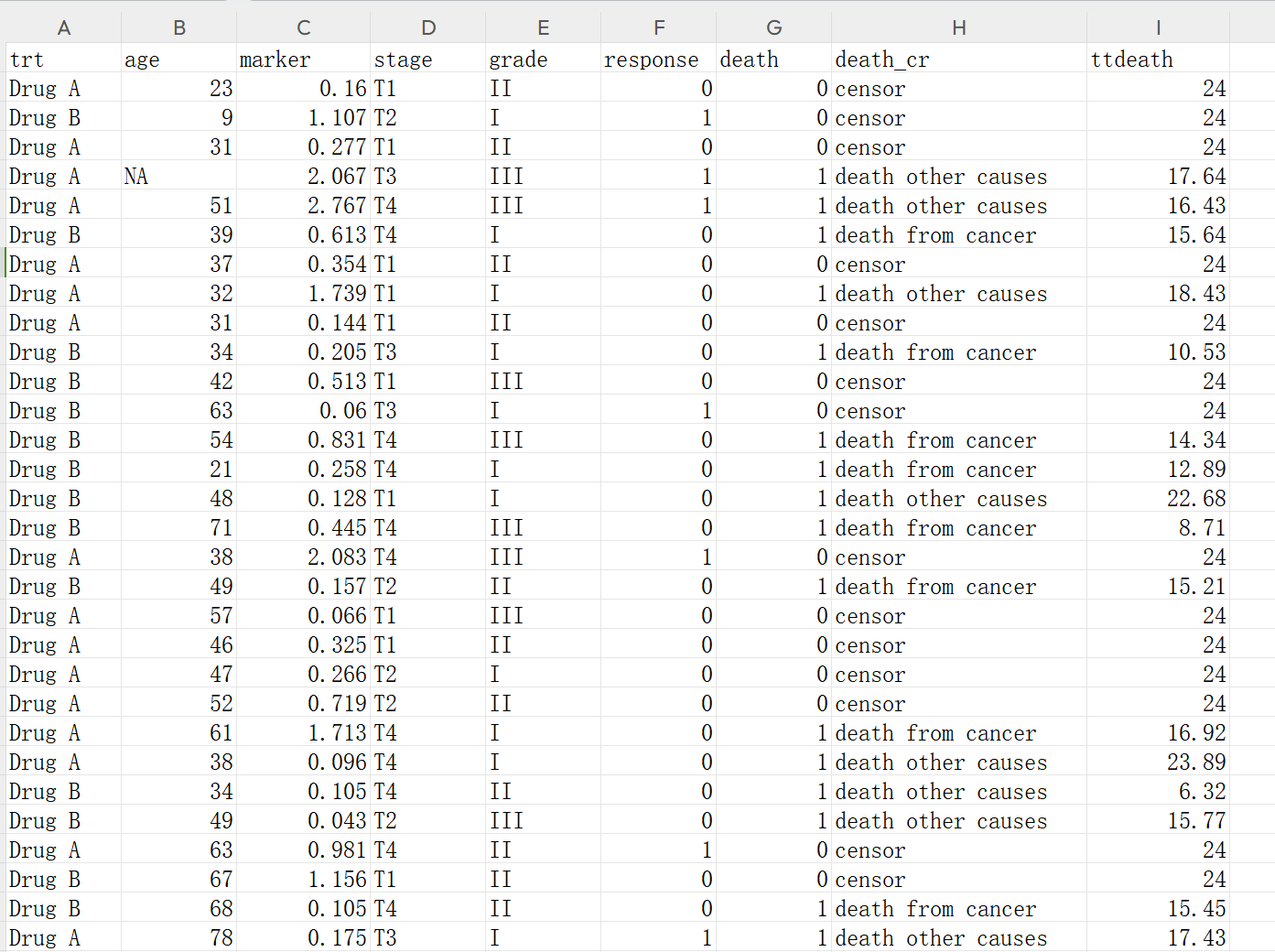
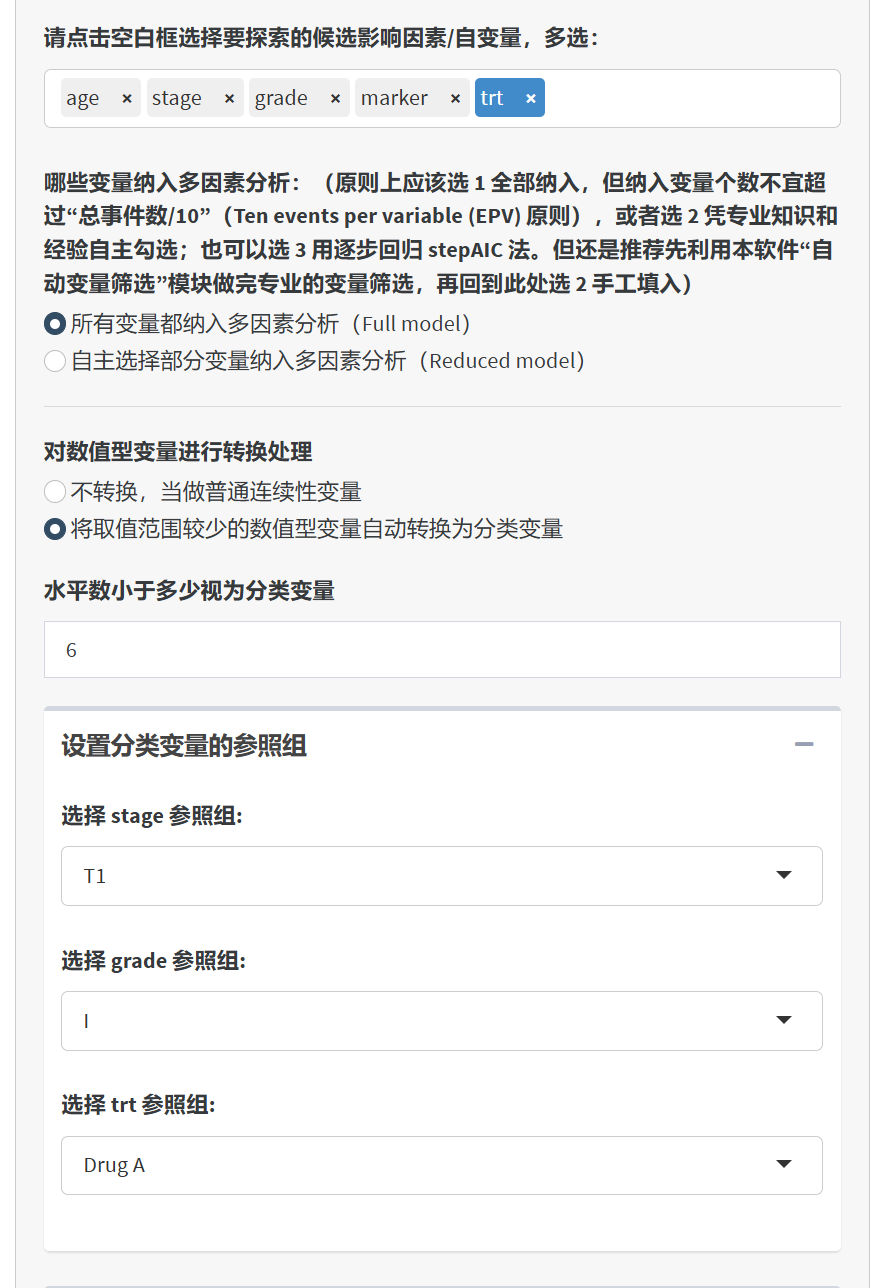
该数据集包含了一组患者的临床信息及其随访结果,主要用于竞争风险模型的分析。数据集中包含了患者的治疗方案、年龄、生物标志物、疾病分期、病理等级、治疗响应、死亡情况及随访时间等变量。以下是各变量的详细说明:
trt: 患者接受的治疗方案(Drug A 或 Drug B)
age: 患者的年龄
marker: 生物标志物水平
stage: 疾病分期(T1, T2, T3, T4)
grade: 等级(I, II, III)
response: 对治疗的响应情况(0:无响应,1:有响应)
death: 死亡情况(0:存活,1:死亡)
death_cr: 死亡的具体原因(censor:无事件,death from cancer:死于癌症,death other causes:死于其他原因)
ttdeath: 发生事件的时间(以月为单位)
5.5.8 数据准备指导
用户在准备自己的数据集进行竞争风险分析时,需要特别注意结局变量和时间变量的构建。以下是具体的准备步骤和要求:
结局变量(Outcome Variable)
事件类型变量:如上述数据集中的
death_cr,该变量应明确标识出每个样本的结局类型。通常包含以下几种情况:主要事件:用户关心的主要事件,例如死于癌症。
竞争事件:可能影响主要事件分析的其他事件,例如死于其他疾病。
删失(censoring):随访结束时未发生任何事件。
时间变量(Time Variable)
随访时间:如上述数据集中的
ttdeath,该变量应记录从基线时间(如诊断日期、治疗开始日期等)到事件发生或随访结束的时间。时间单位可以是天、月或年,但需在分析前明确说明。如果发生了事件,则填发生事件的时间,如果没有发生事件(censor),则填最后一次随访时间。
5.5.9 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“探寻可能的影响因素(多因素分析),所有因素分析结果列入表格(竞争风险模型 Competing Risks Regression)” 进入模块:

5.5.12 选择状态变量
在选择了时间变量后,系统将自动检测数据中水平数较多的分类变量。请选择代表患者最终状态的变量。该变量需要在数据准备阶段被设置为因子型,且至少有三个取值,例如“未发生事件(censor)”,“死于癌症”,“死于其他疾病”。
5.5.19 设置其他选项
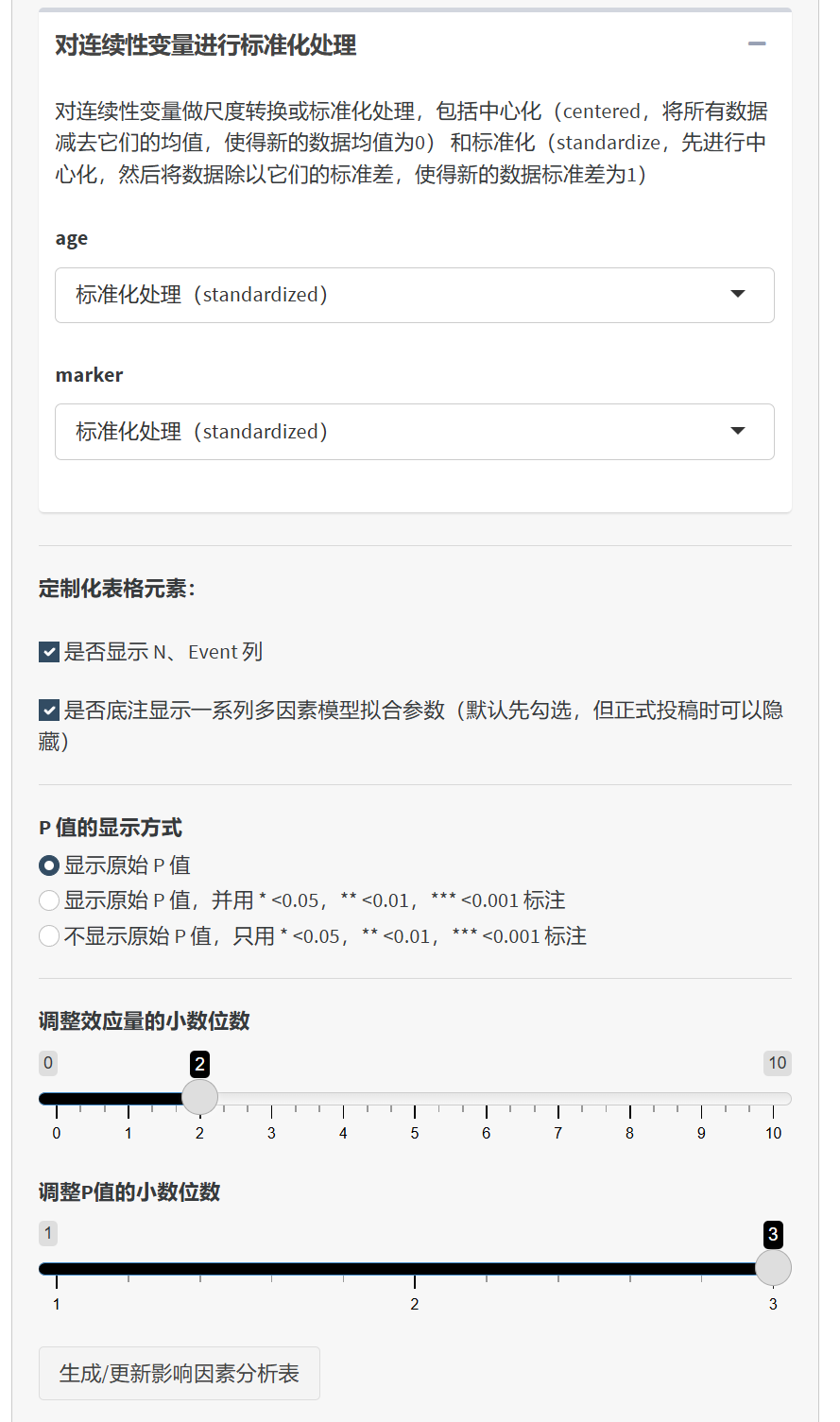
可以选择是否将取值范围较少的数值型变量转换为分类变量。将连续变量根据分位数转换为n等分的分类变量。选择是否显示N、Event列,设置P值显示方式,调整效应量和P值的小数位数。
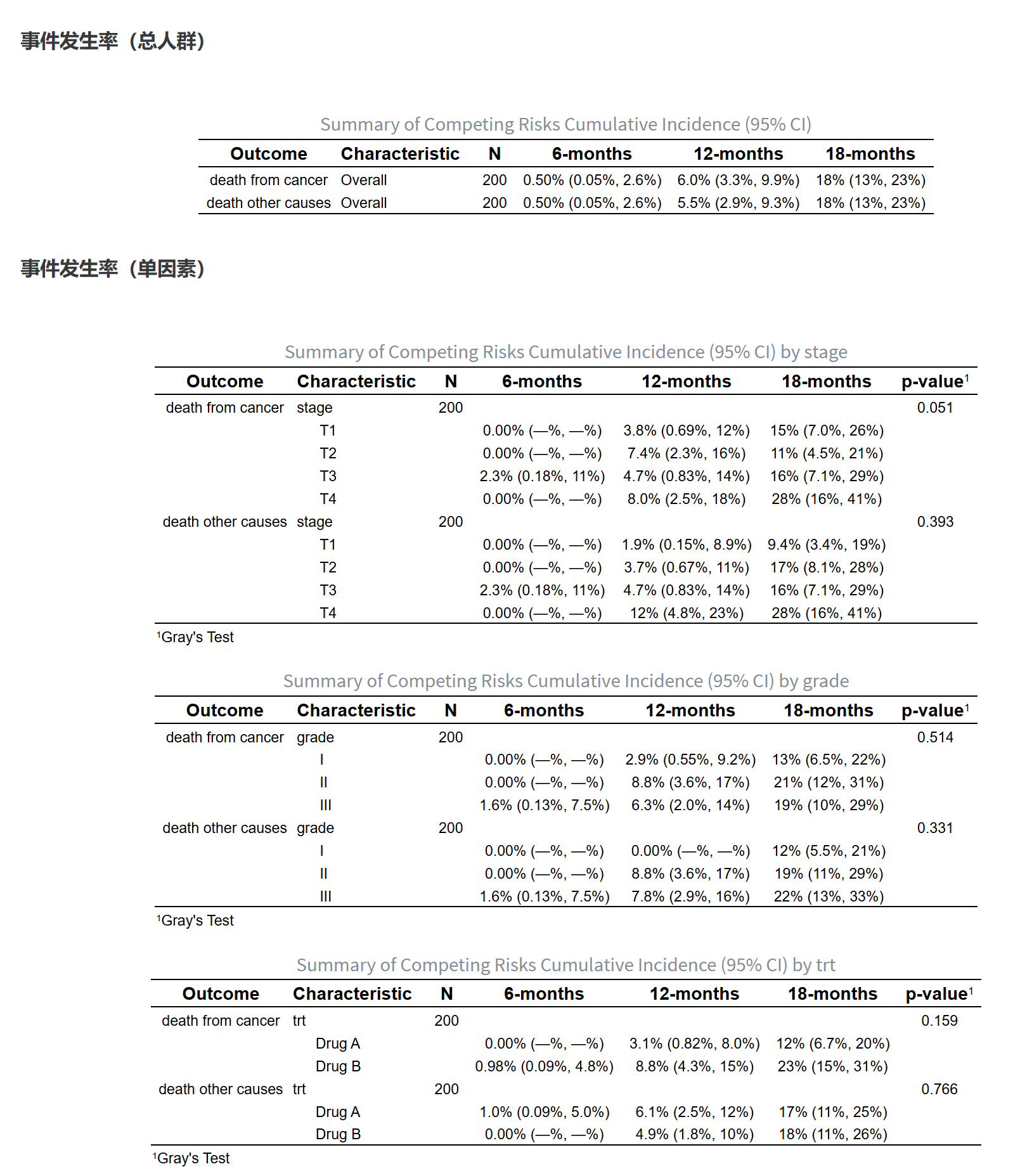
5.5.23 累积发生率分析

5.5.23.2 选择累积发生率表的时间单位
为了生成累积发生率表,您需要选择结果展示的时间单位。系统会根据您的选择自动进行时间单位转换,具体转换规则如下:
1 年 = 365.25 天
1 月 = 30.4375 天
1 周 = 7 天
请在以下选项中进行选择:
天
周
月
年
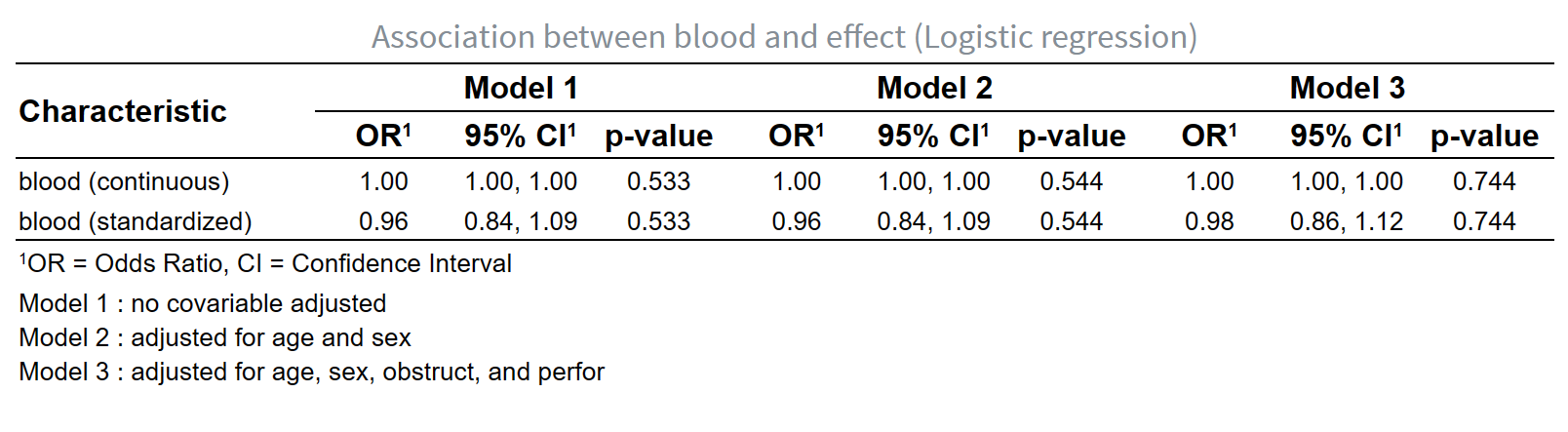
5.6 有明确的感兴趣的研究因素,而混杂因素调整仅在表格底注(一般线性/Logistic/Cox/Poisson回归)
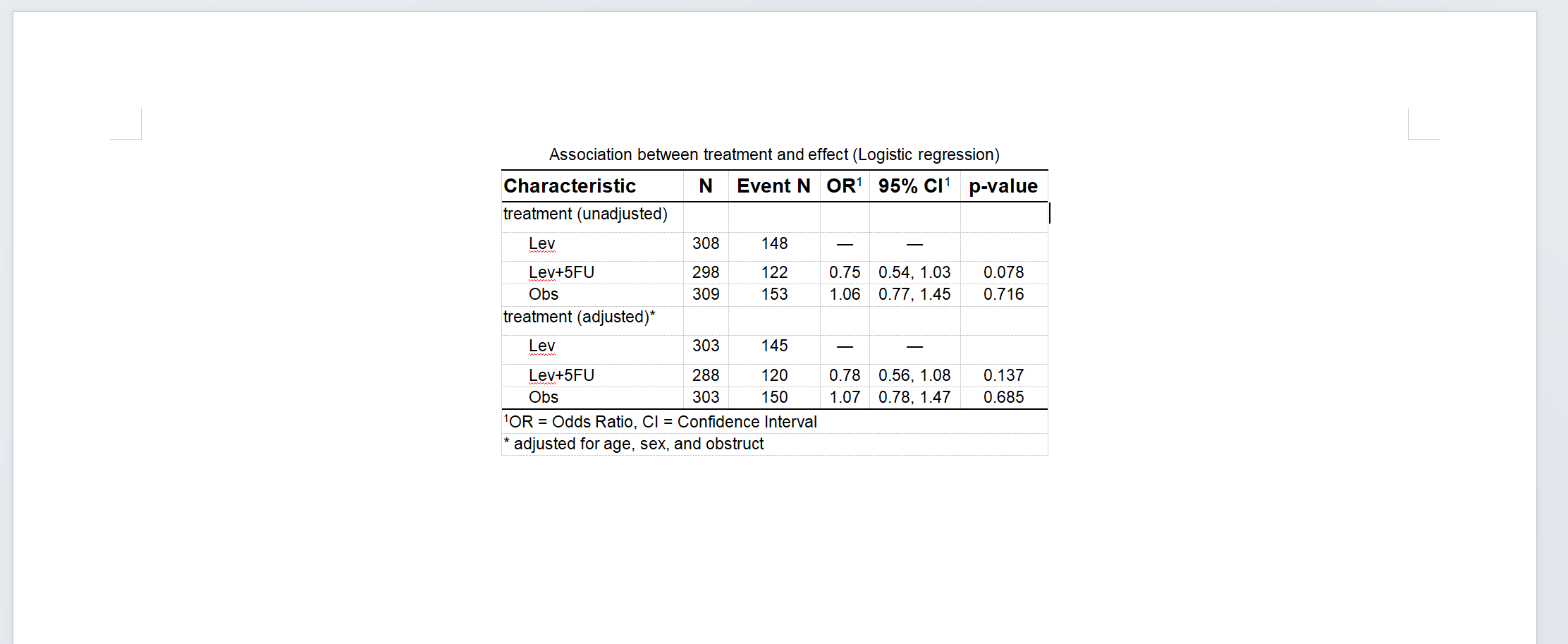
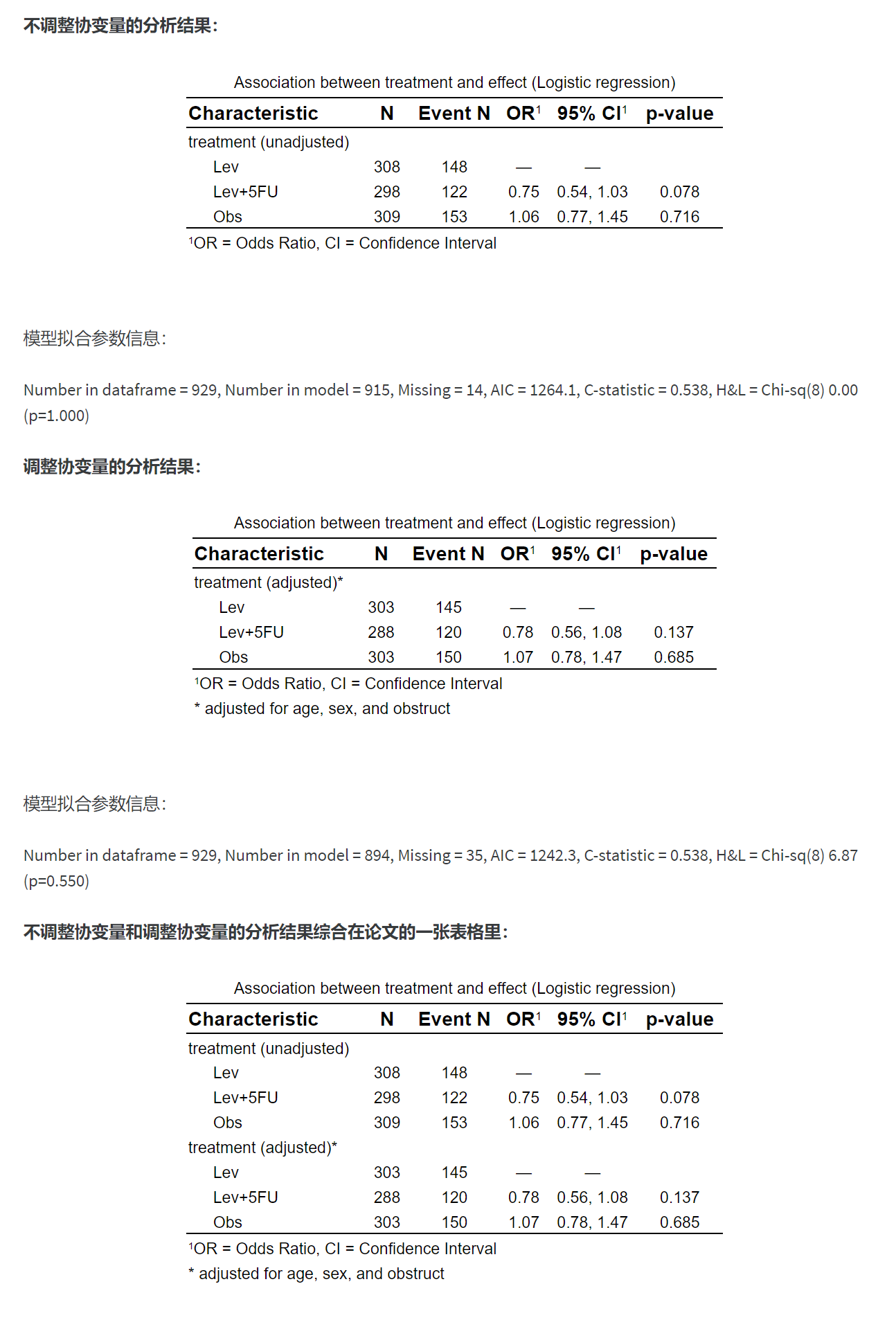
本模块适合做验证性影响因素研究,验证某个影响因素(如治疗分组、或者是否饮酒等)对某个临床结局(事件)的影响,并控制混杂因素或协变量(如性别、年龄、基线血糖等等)。
所谓 “验证性”,是指研究开始已经有明确的目的,特定要研究某个固定的感兴趣的影响因素,而其他影响因素仅作为协变量处理,不展开讨论。
主要特点:
根据上传的科研数据,简单点击设置后,自动完成不调整协变量和调整协变量的回归分析
支持线性回归、Logistic 回归、Cox 回归、Poisson 回归
支持一键自动把连续性变量拆分成分类变量,如 Q1、Q2、Q3、Q4 等
支持一键把连续性变量做标化、取对数等
生成 word 统计报告,自动生成 Title, Objective, Methods 和 Results, 生成 SCI 期刊标准统计表格
5.6.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.6.2 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“有明确的感兴趣的研究因素,而混杂因素调整仅在表格底注(一般线性/Logistic/Cox/Poisson回归)” 进入模块:
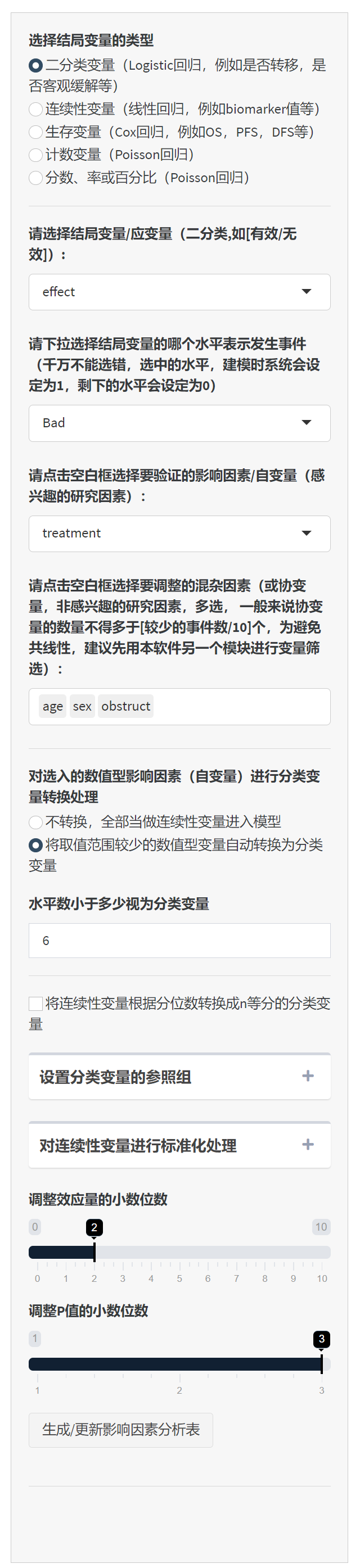
5.6.3 选择结局变量
机器人根据结局变量的类型来选择分析方法。二分类变量,系统会选择logistic回归,如果是连续性变量,系统会选择一般线性回归。如果是生存变量Time和Status的组合,系统会采用Cox回归。如果是计次计数变量,系统会选择Poisson回归,当然如果是率或者百分比,也会采用Poisson/负二项回归。
5.6.6 连续性变量拆成分类变量
连续性变量需要拆成分类变量的场景有:
- 本身就是一个分类变量,如 I 期,II 期,III 期,IV 期等,只不过用了数字1,2,3,4来表示,这可以在前面筛选变量的界面直接把它设置为分类变量(factor)即可。
前面如果忘记了,或者不方便,这里提供了一个功能,可以设置唯一取值数小于多少个水平的变量,全部转换成分类变量。例如只有5个取值 (比如只有数字1-5可取)以下的变量,全部批量转换成分类变量;
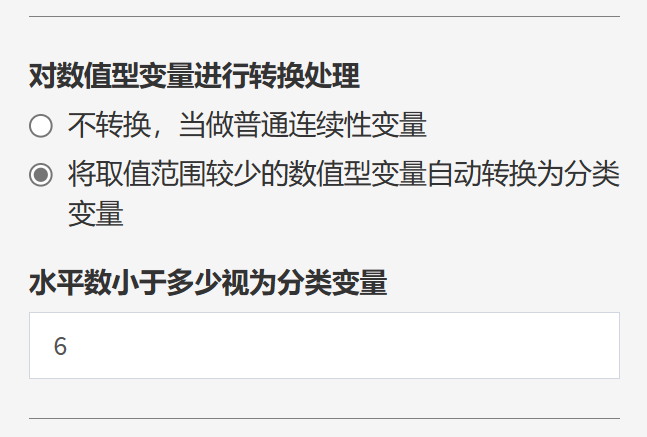
如上图,对于只能取值6以下的变量,统统变成分类变量。
- 本身是连续性变量,例如年龄、血糖等等,但需要转换成 低、高的二分类变量,或低、中、高的三分类变量,或Q1,Q2,Q3,Q4的四分位数分类变量,这里也提供了一个自动化转换工具,可以根据患者数量,平均拆分成N个组。
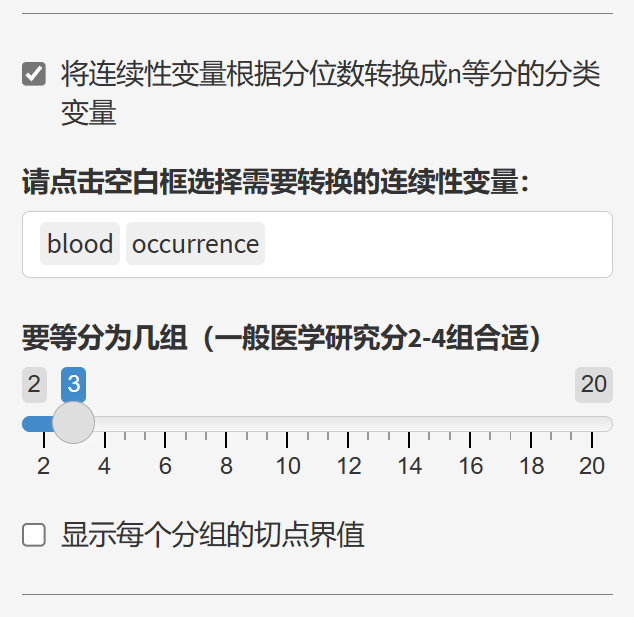
如上图,将blood和occurrence两个连续性变量,切成三等分的分类变量
显示了切割分界点的界值。
多大支持切割成20组,因为更多分组没有太大医学价值。
如果需要更强大的分组功能呢,例如自定义切割点,如<10岁,>65岁等,或者用K-means 聚类分组等,可以去本软件的 准备数据 模块,选择”数据离散化” 模块进行复杂的分组操作。
5.7 有明确的感兴趣的研究因素,调整不同个数混杂因素,进行多模型比较的套路分析(一般线性/Logistic/Cox/Poisson回归)
5.7.3 引言
在医学统计分析中,我们经常要评估各种因素如何影响某个特定的健康结局。这些因素可以是生活习惯(如抽烟、饮酒)、遗传倾向、疾病状态(如心脏病)、环境暴露或者医疗干预(如药物治疗)。为了理解这些影响因素(或自变量)与健康结局(或因变量)之间的关系,研究者会运用多种统计回归模型来分析数据。
回归分析是一种强大的统计工具,它可以揭示一个或多个自变量对一个因变量的影响。根据因变量的类型和研究的需求,可以选择不同类型的回归分析:
逻辑回归(Logistic regression)适用于二分类结果变量,如疾病有无。
线性回归(Linear regression)适合连续结果变量,如血压或胆固醇水平。
Cox回归(Cox proportional hazards regression)用于分析生存时间数据,即时间到一个事件(如死亡或复发)的发生。
Poisson 回归 适用于计数数据或事件发生率的分析。
研究者会拟合多个模型来比较的原因是,这可以帮助他们理解在控制了其他变量(如性别、年龄等)后,主要自变量(如抽烟)的独立效应是否仍然显著。这也有助于识别和校正混杂因子的影响,这些混杂因子可能扭曲了主要自变量和结果变量之间的真实关系。
例如,在研究抽烟是否增加心脏病风险的研究中,一个简单的模型可能只考虑抽烟的影响。而更复杂的模型可能会加入年龄、性别、饮食和运动等协变量。通过比较这些模型,研究者可以更好地了解在不同情境下抽烟和心脏病风险之间的关系。
为了判断模型的效度,研究者会查看比值比(Odds Ratio)、风险比(Hazard Ratio)或回归系数,以及它们的统计显著性(p-value)和置信区间(Confidence Interval, CI)。如果在多个模型中,这些统计量保持稳定,这增加了研究结果的可靠性。
综上所述,通过拟合和比较多个模型,研究者可以更全面地评估影响因素对健康结局的影响,这为制定预防策略和治疗干预提供了科学依据。
5.7.4 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.7.5 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“有明确的感兴趣的研究因素,调整不同个数混杂因素,进行多模型比较的套路分析(一般线性/Logistic/Cox/Poisson回归)” 进入模块
5.7.6 操作步骤
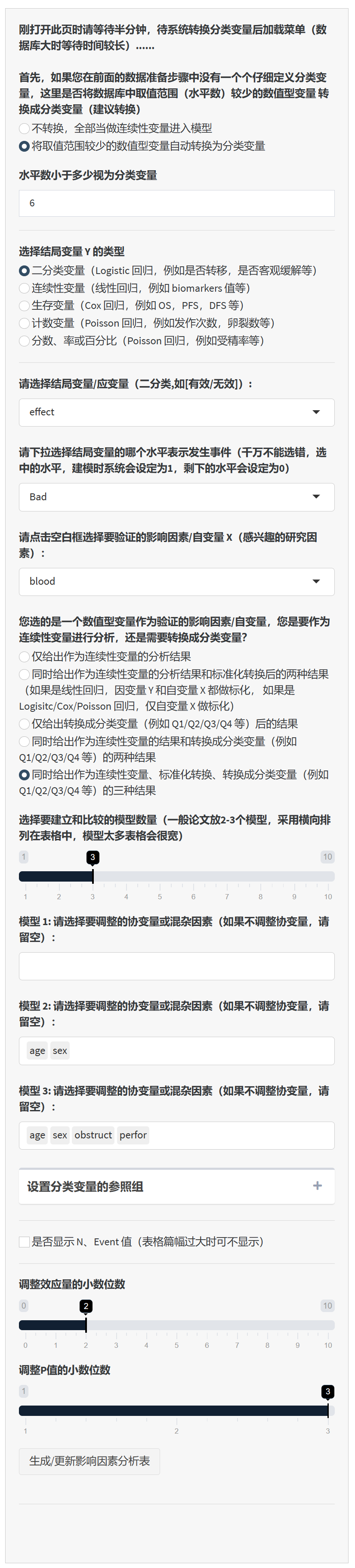
5.7.6.2 等待数据转换
- 打开页面后,请耐心等待半分钟让系统处理并加载您的数据。如果您的数据库较大,这个过程可能需要更长时间。系统会自动把水平数低于6的数值型变量转换为分类变量,当然您也可以手动改回来不做转换
5.7.6.3 选择模型类型
- 接下来,您需要根据结局变量的类型选择合适的模型。可选的模型包括二分类变量(Logistic回归)、连续性变量(线性回归)、生存变量(Cox回归)、计数变量(Poisson回归)等。
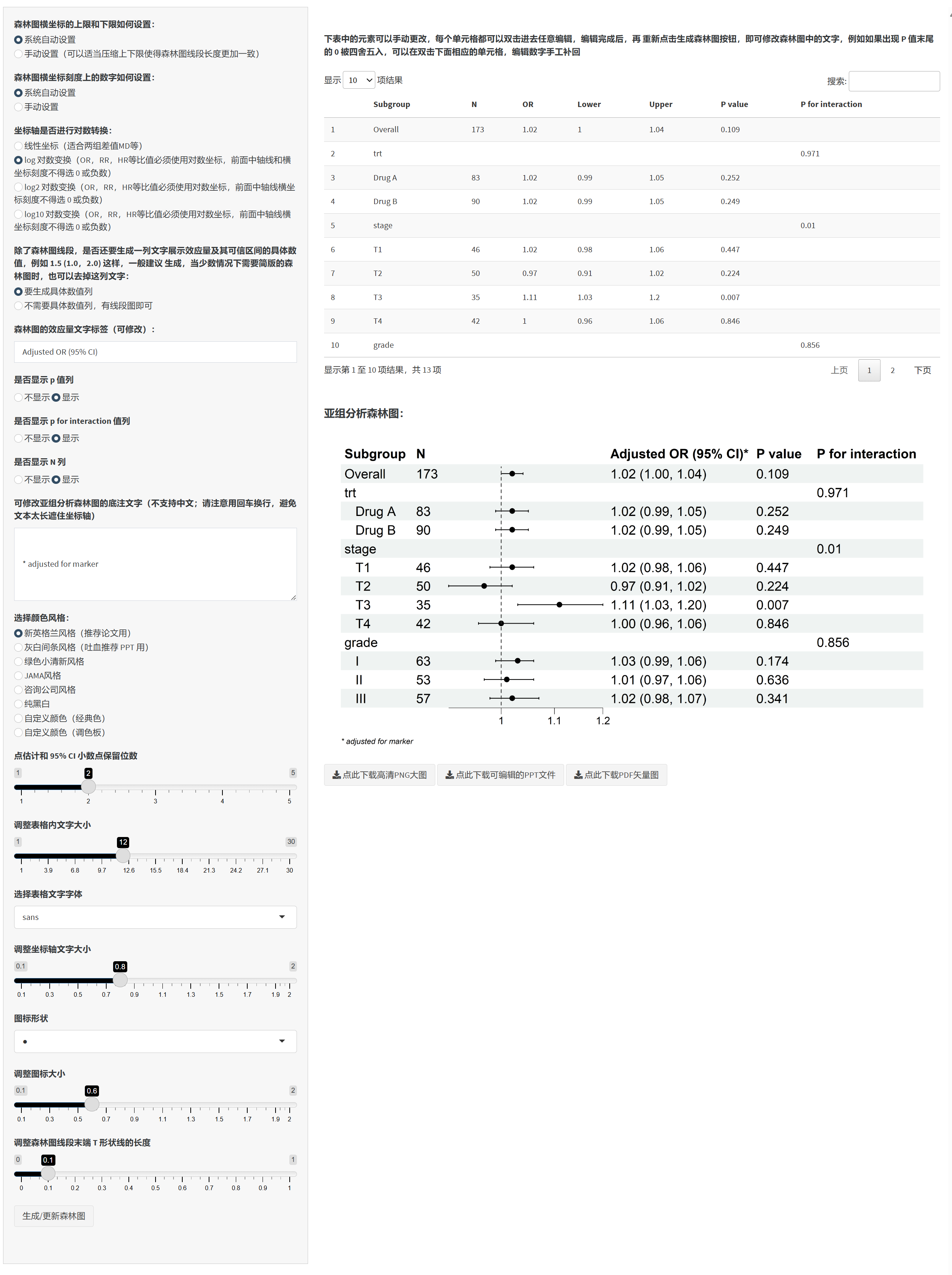
5.8 回归分析的亚组(分层)分析
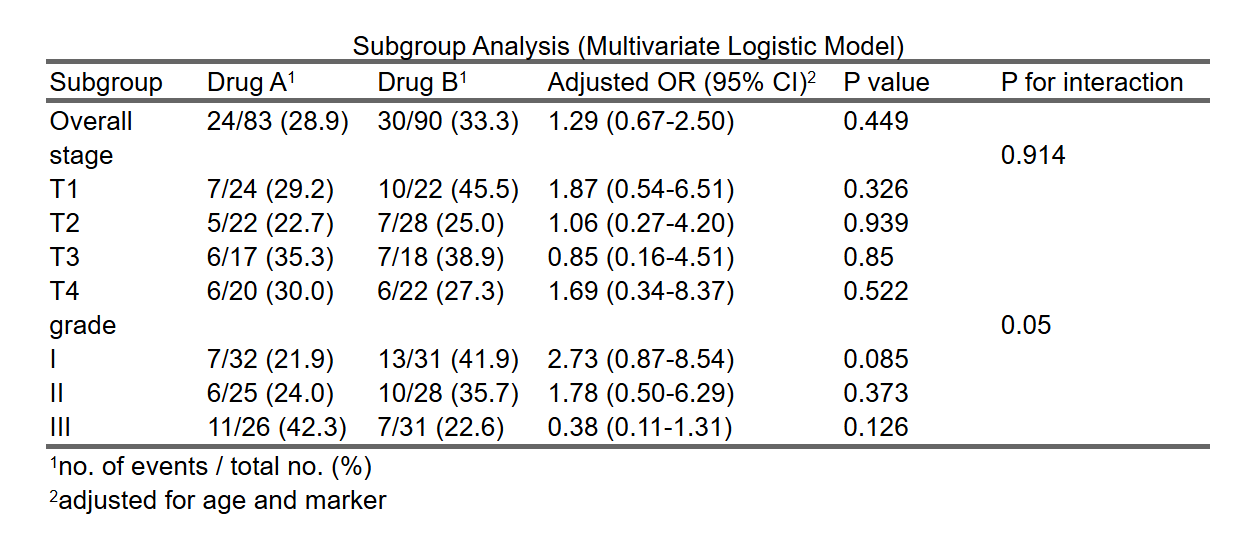
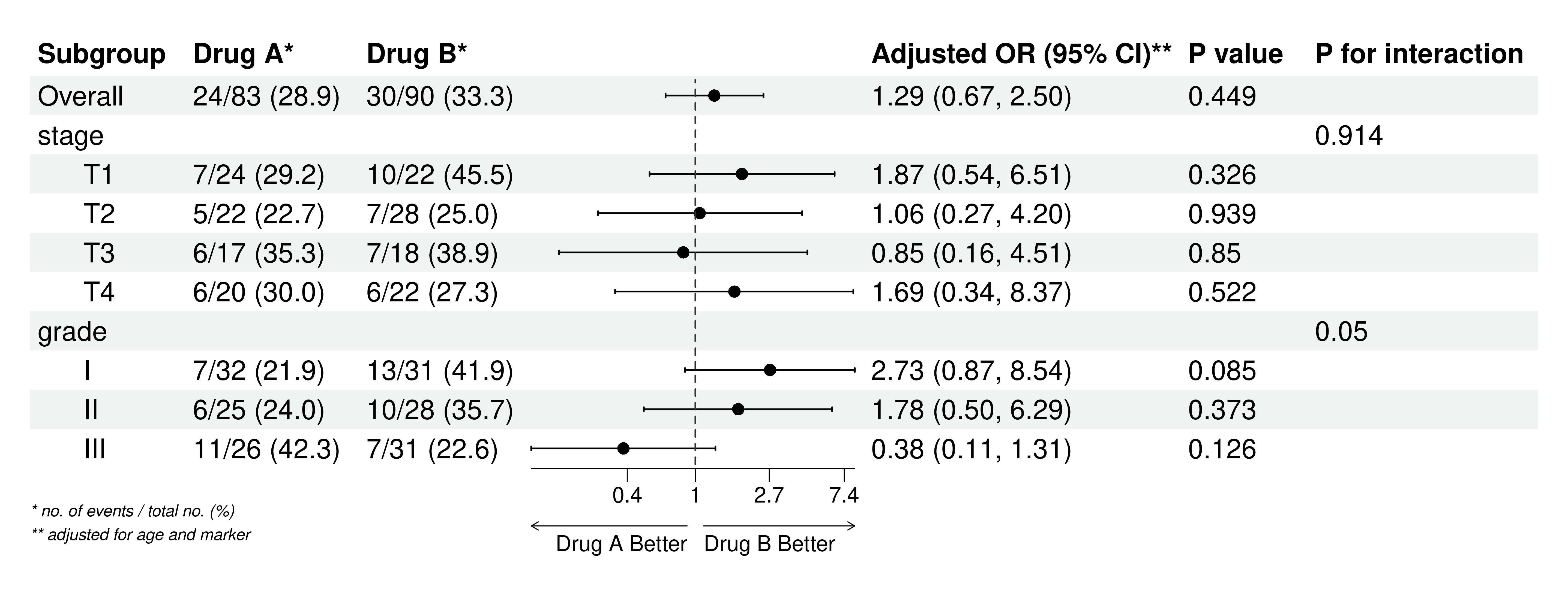
应变量为是否恶化,自变量为 A 组 B 组:
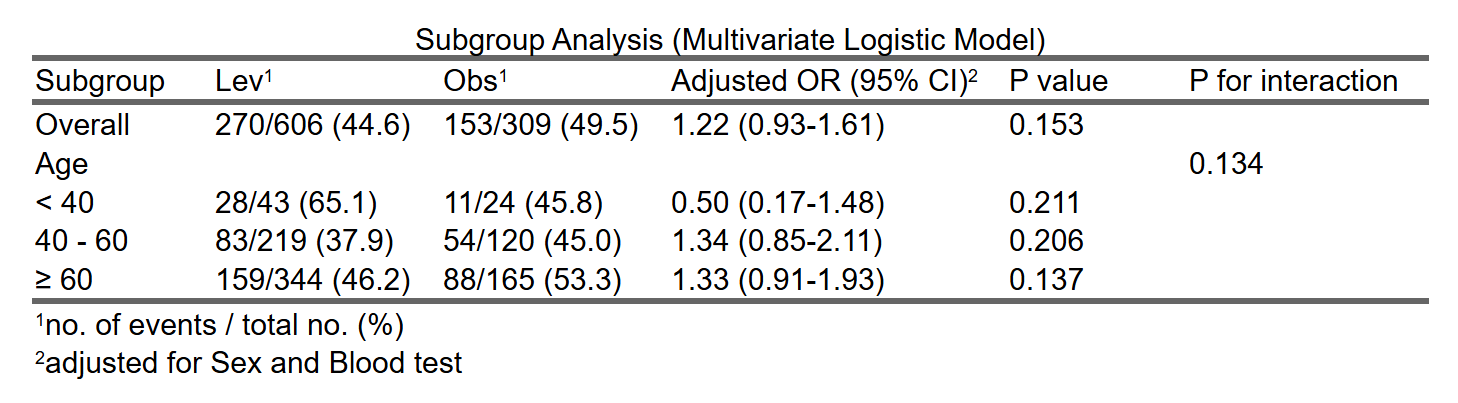
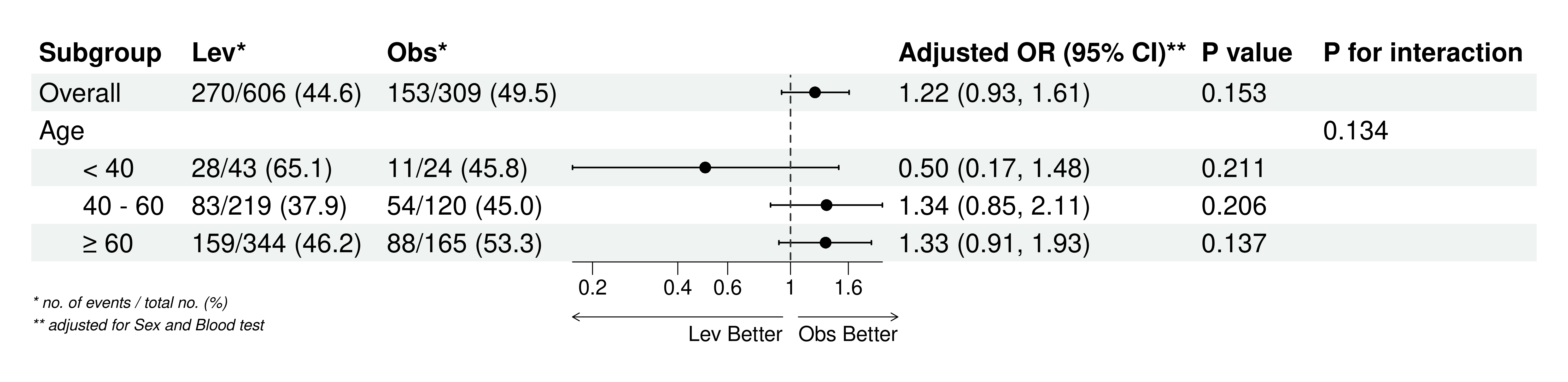
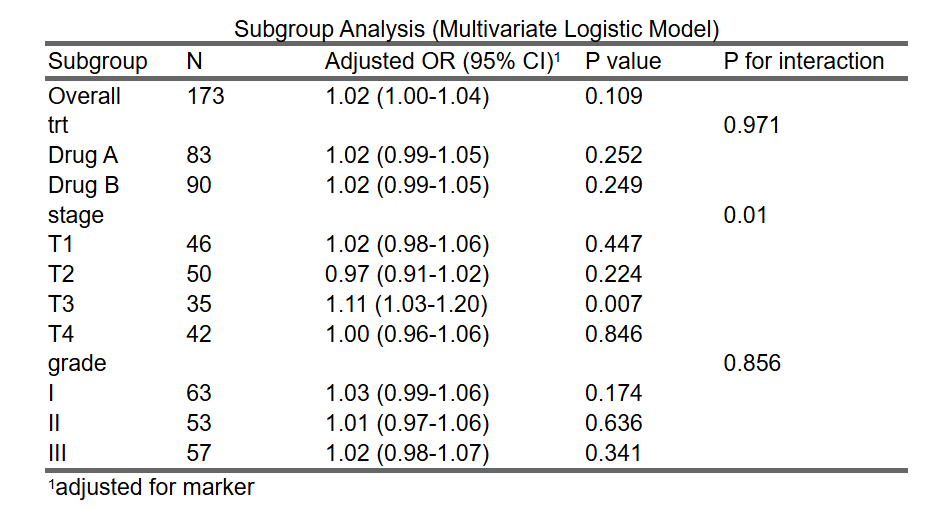
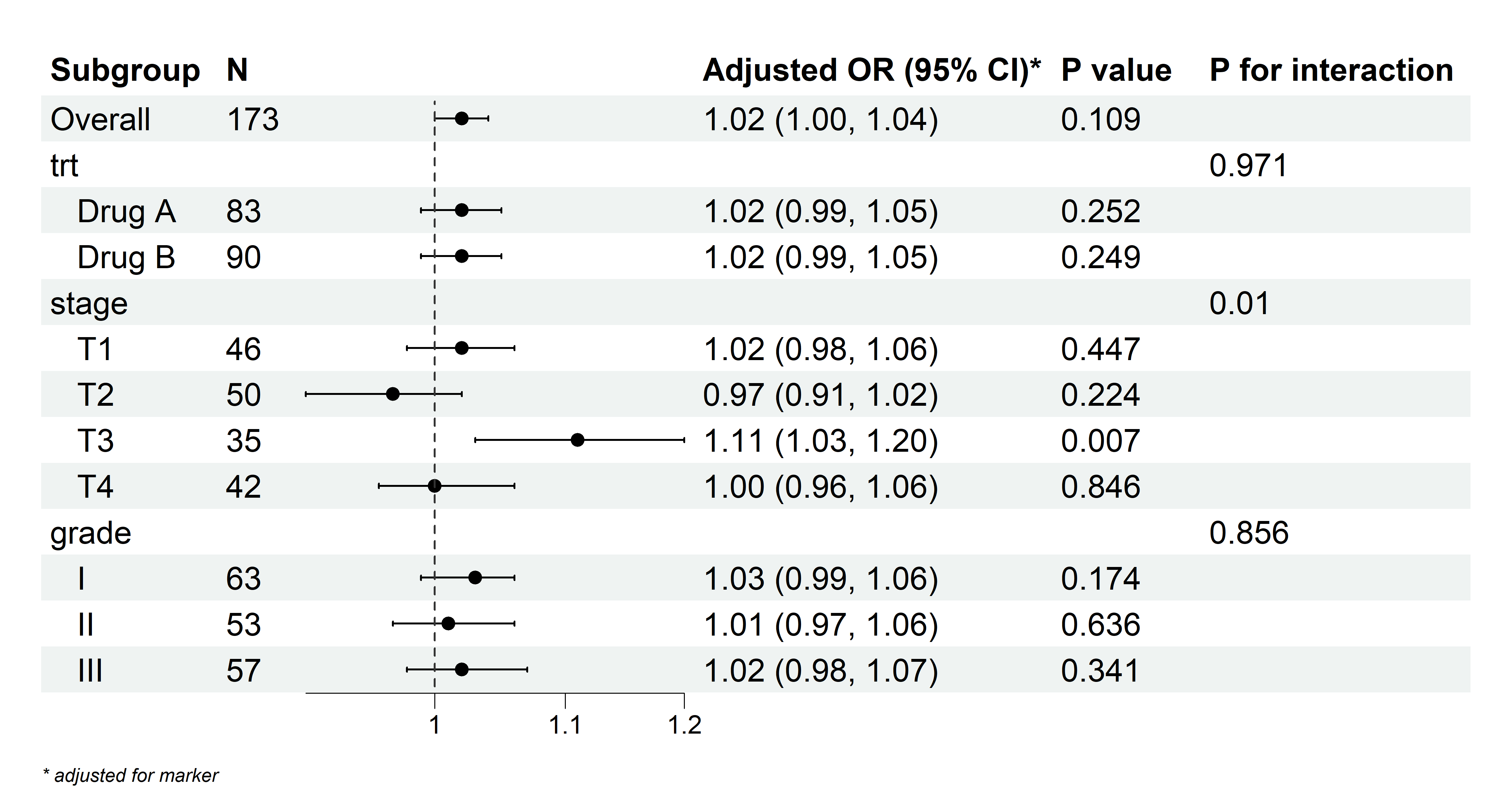
应变量为是否恶化,自变量为 连续性变量(年龄):
5.8.1 亚组(分层)分析的定义和概念
亚组分析是指在总体研究样本中,根据某些特征将样本划分为若干亚组,并在每个亚组内进行独立的分析。其目的是探讨不同亚组在某些特定特征下的差异,揭示出整体分析中可能被忽视的细节。亚组分析通常应用于回归分析之后,以进一步细化研究结果,使其更具针对性和实用性。
5.8.2 为什么回归分析之后要做亚组分析?
虽然回归分析可以揭示总体样本的趋势和关系,但不同特征(如年龄、性别、疾病分期等)可能对结果有不同的影响。通过亚组分析,我们可以:
识别异质性:揭示不同亚组之间的差异,识别是否存在某些亚组对治疗或干预有不同的反应。
提高结果的外推性:通过细分亚组,研究结果更能代表不同特征人群,提高其外推性。
制定个性化治疗策略:在医学研究中,不同亚组的患者可能需要不同的治疗方法,亚组分析可以帮助制定更为精准的治疗策略。
5.8.3 医学研究的例子
5.8.3.1 自变量为二分类变量的例子
例如,在一项研究中,探讨两种药物(药物A和药物B)对某种疾病的治疗效果。研究者首先进行总体样本的回归分析,得出药物A和药物B在总体人群中的效果。然而,考虑到疾病的分期和等级可能影响药物效果,研究者进一步进行亚组分析,将样本根据疾病的分期(如T1、T2、T3、T4)和等级(如I、II、III)分为不同亚组,分别分析各亚组内两种药物的效果。
通过亚组分析,研究者发现:
在疾病分期为T1的亚组中,药物A的效果优于药物B。
在等级为I的亚组中,药物B的效果显著优于药物A。 这种细化的分析结果可以帮助医生根据患者的具体情况选择更合适的药物。
5.8.3.2 自变量为连续变量的例子
例如,在一项研究中,探讨患者的血糖水平(一个连续变量)对心脏病风险的影响。研究者首先进行总体样本的回归分析,得出血糖水平与心脏病风险之间的关系。然而,考虑到不同性别和年龄段可能影响血糖水平与心脏病风险之间的关系,研究者进一步进行亚组分析。
研究者将样本按性别(男性和女性)和年龄段(如年轻组、中年组和老年组)分为不同亚组,然后分别分析在不同亚组中,血糖水平对心脏病风险的影响。
通过这种分析,研究者可能会发现:
在男性老年组中,血糖水平较高与心脏病风险显著增加相关。
在女性年轻组中,血糖水平与心脏病风险之间没有显著相关性。
这种分析有助于了解在不同性别和年龄段中,血糖水平对心脏病风险的具体影响,从而帮助制定更加个性化的预防和治疗策略。
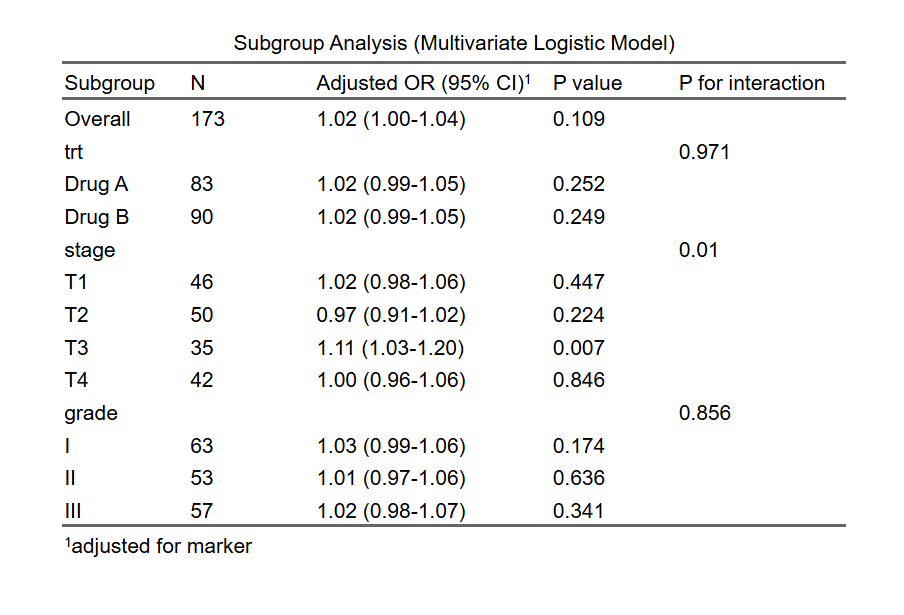
5.8.4 P 值和 P for interaction 的意义
在亚组分析中,P 值和 P for interaction 是两个重要的统计指标:
P 值:在每个亚组内,P值用于检验在该亚组中自变量(如血糖水平)与结果变量(如心脏病风险)之间的关系是否显著。P值越小,说明关系越显著。通常,P值小于0.05被认为有统计学显著性。
P for interaction:P for interaction用于检验不同亚组之间的效果是否有显著差异。它衡量的是自变量(如血糖水平)与亚组变量之间的交互作用。如果P for interaction值小于0.05,说明不同亚组间的效果差异具有统计学显著性,这意味着血糖水平对心脏病风险的影响在不同亚组中有显著差异。
总之,亚组分析通过细化研究对象,揭示了不同特征人群的差异,帮助制定更为精准的治疗策略。P值和P for interaction则为这种差异提供了统计学依据,使研究结果更为可靠和科学。
5.8.5 关于多重比较的补充与如何调整
在事后(post-hoc)进行亚组分析、且一次性做了多种亚组或多次检验时,第一类错误(把原本不存在的差异误判为显著)的总体概率会被放大。此时,单纯以“P < 0.05”为阈值不再稳妥,应进行多重比较调整。需要考虑校正的情形包括:
同一结局下同时考察多个亚组(年龄、性别、合并症、分期……);
对同一亚组变量做了多个切点/多种分组方式(如三分位、四分位、不同阈值);
同时做了多个交互作用检验(多个潜在效应修饰因子);
多个结局/多个时间点的并行比较。
5.8.5.2 常用调整策略
Bonferroni:将显著性水平按检验次数 m 均分(α* = α / m),或报告 p* = p × m。简单但偏保守。
Holm(顺序 Bonferroni):按 P 值从小到大排序,逐步比较阈值 α/(m−i+1)。通常优于简单 onferroni。
Hochberg:类似顺序法(对部分情形更有力),但使用条件略严苛。
FDR 控制(错误发现率):适合探索性亚组筛查、亚组数量较多的情形。
Benjamini–Hochberg(BH):输出 q 值(FDR-adjusted P)。常用阈值 q < 0.05 或 0.10。
相比 FWER,FDR 更容易发现真正阳性,但允许一定比例的“发现”为假阳性。
5.8.6 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.8.7 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“回归分析的亚组(分层)分析(支持连续性或二分类的自变量)(一般线性/Logistic/Cox/Poisson回归)” 进入模块:
5.8.8 选择结局变量的类型
进入软件后,选择“回归分析”模块。
在“选择结局变量的类型”部分,根据您的研究需求,选择适合的回归模型:
二分类变量(Logistic回归,例如是否转移,是否客观缓解等)
连续性变量(线性回归,例如生物标志物值等)
生存变量(Cox回归,例如总生存期(OS),无进展生存期(PFS),无病生存期(DFS)等)
5.8.9 选择结局变量/应变量
根据您在第一步选择的结局变量类型,进行相应的操作:
Logistic回归:
系统会自动筛选数据库中所有的二分类变量。
在“请选择结局变量/应变量”下拉菜单中,选择您的结局变量。
线性回归:
系统会自动筛选数据库中所有的连续性变量。
在“请选择结局变量/应变量”下拉菜单中,选择您的结局变量。
Cox回归:
系统会自动筛选数据库中所有的连续性变量。
在“请选择代表时间的变量”下拉菜单中,选择表示时间的变量(如从开始到死亡的时间,或从开始到末次随访时间)。
系统会自动筛选数据库中所有的二分类变量。
在“请选择代表患者最终状态的变量”下拉菜单中,选择表示患者最终状态的变量(如1代表发生事件,0代表删失)。
5.8.10 选择结局变量的水平
Logistic回归和Cox回归:
系统会自动检测结局变量的所有水平。
在“请下拉选择结局变量的哪个水平表示发生事件”下拉菜单中,选择表示发生事件的水平(注意:选中的水平在建模时系统会设定为1,剩下的水平会设定为0)。
5.8.11 选择解释变量/自变量
在“要研究的解释变量/自变量的类型”部分,选择变量类型:
二分类变量
连续性变量
系统会根据您的选择筛选相应的变量。
在“请点击选择要研究的解释变量/自变量”下拉菜单中,选择您的解释变量/自变量。
5.8.12 选择参照组和观察/试验组(仅针对二分类解释变量)
系统会自动检测解释变量的所有水平。
在“请下拉选择参照组”下拉菜单中,选择参照组。
在“请下拉选择观察/试验组”下拉菜单中,选择观察/试验组。
5.9 将一个连续性变量的不同取值设为分割点进行分层,进行敏感性亚组(分层)分析
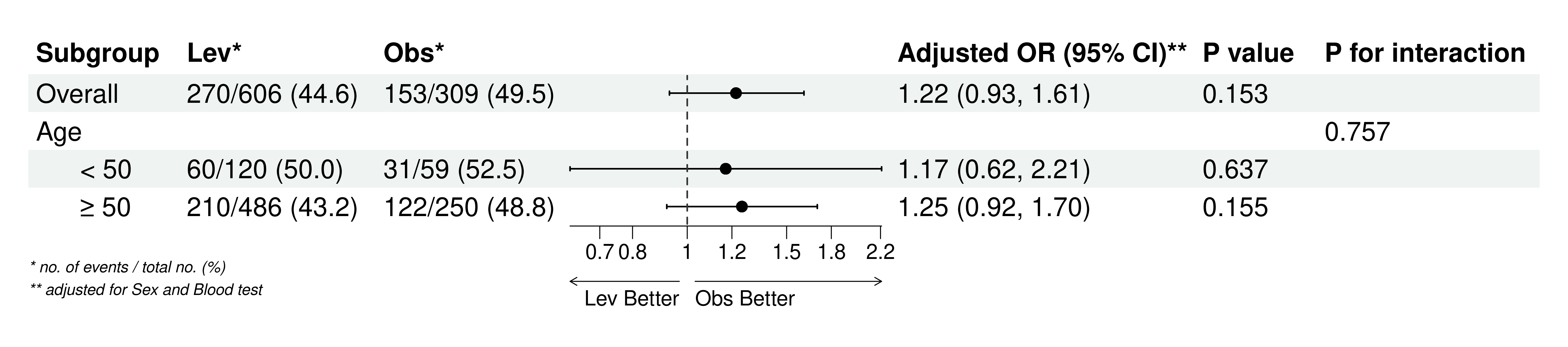
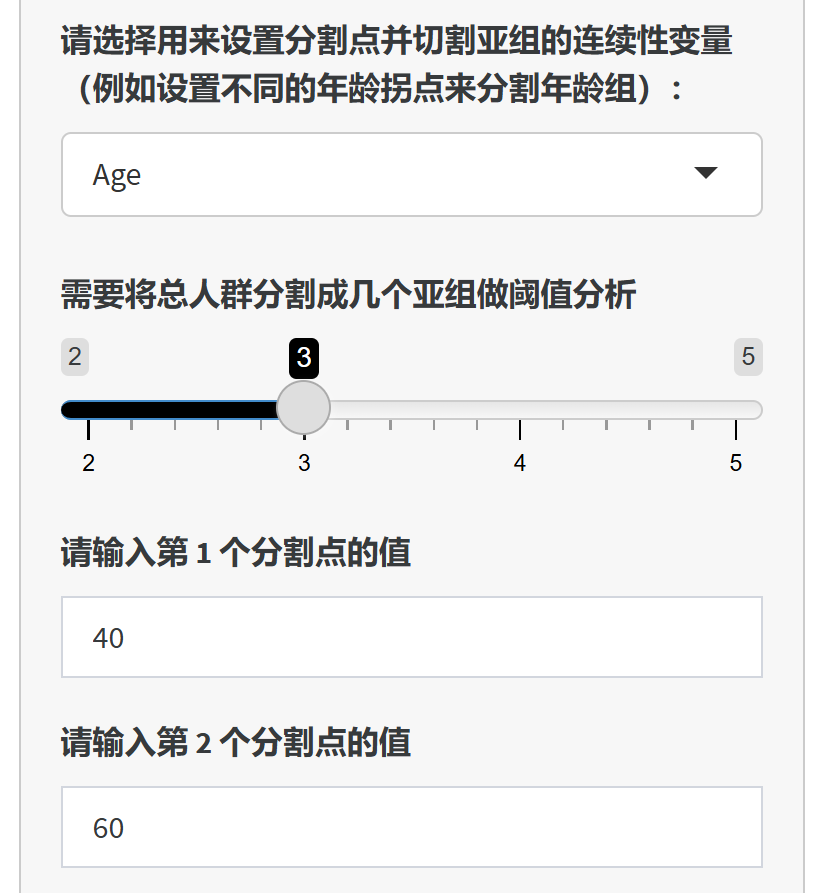
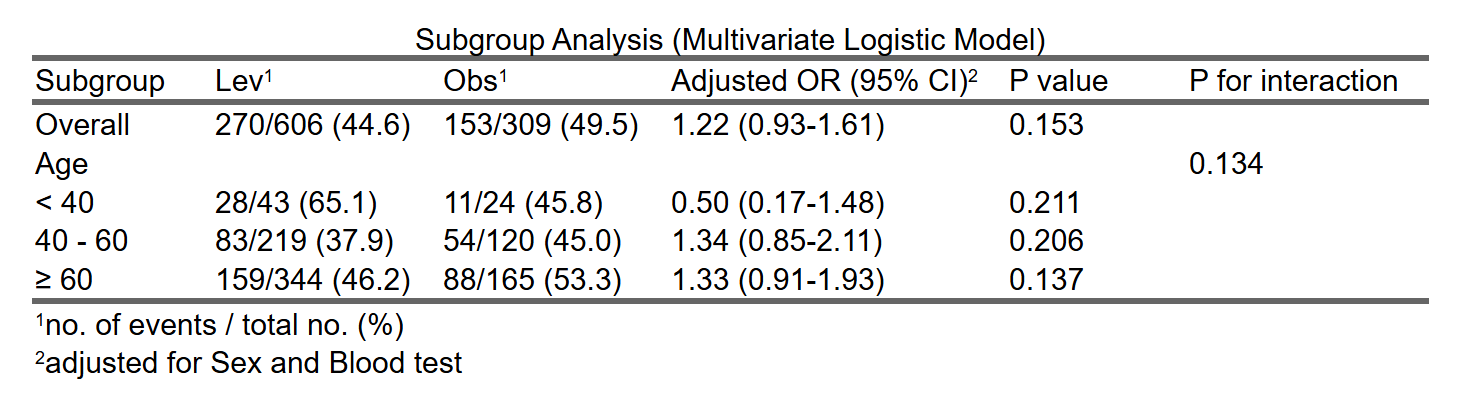
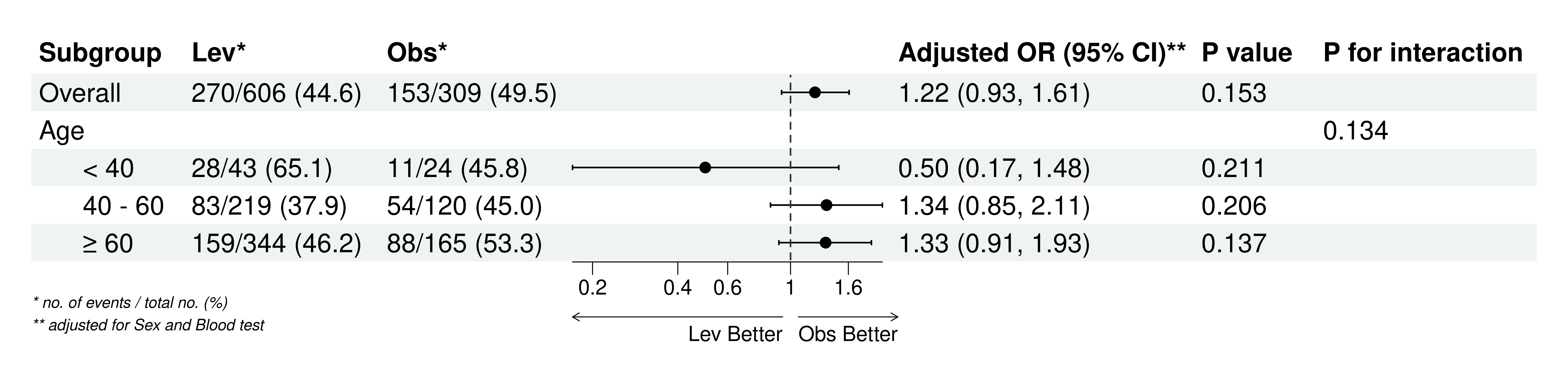
设定不同的分割点,用一个连续性变量的值(例如年龄),将数据分成几个亚组,做回归分析的亚组(分层)分析:
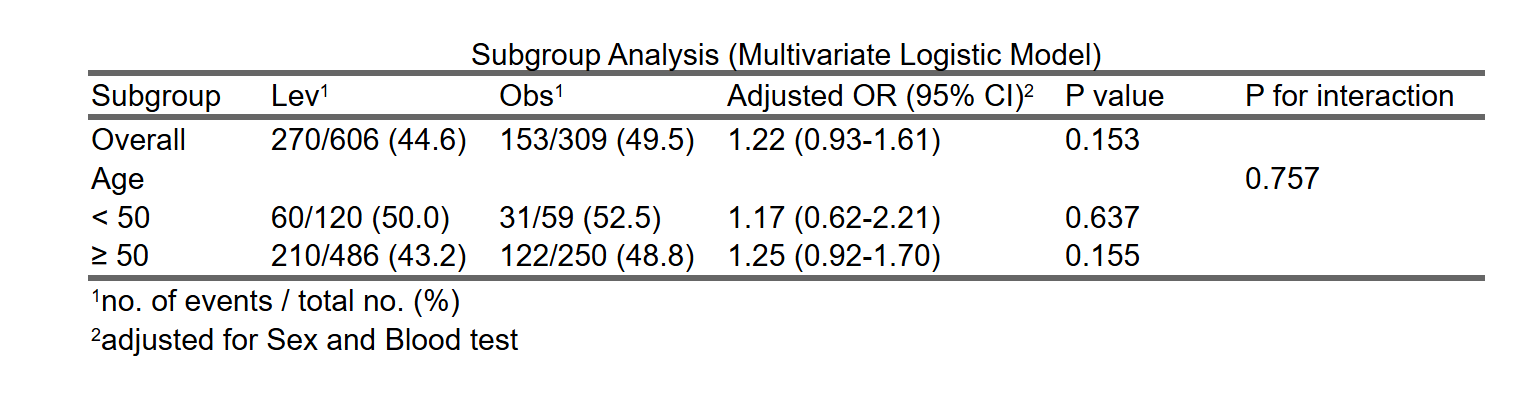
5.9.1 亚组(分层)分析的定义和概念
亚组分析是指在总体研究样本中,根据某些特征将样本划分为若干亚组,并在每个亚组内进行独立的分析。其目的是探讨不同亚组在某些特定特征下的差异,揭示出整体分析中可能被忽视的细节。亚组分析通常应用于回归分析之后,以进一步细化研究结果,使其更具针对性和实用性。
5.9.2 为什么回归分析之后要做亚组分析?
虽然回归分析可以揭示总体样本的趋势和关系,但不同特征(如年龄、性别、疾病分期等)可能对结果有不同的影响。通过亚组分析,我们可以:
识别异质性:揭示不同亚组之间的差异,识别是否存在某些亚组对治疗或干预有不同的反应。
提高结果的外推性:通过细分亚组,研究结果更能代表不同特征人群,提高其外推性。
制定个性化治疗策略:在医学研究中,不同亚组的患者可能需要不同的治疗方法,亚组分析可以帮助制定更为精准的治疗策略。
5.9.3 当分组变量不是一个现成的分类变量,而是一个连续性变量,怎么做亚组(分层)分析?
例如,在一项研究中,探讨两种药物(药物A和药物B)对某种疾病的治疗效果。研究者首先进行总体样本的回归分析,得出药物A和药物B在总体人群中的效果。然而,考虑到疾病的分期和等级可能影响药物效果,研究者进一步进行亚组分析,如果已经有现成的分类变量,例如疾病的分期(如T1、T2、T3、T4)和等级(如I、II、III),则可以直接用这样的亚组,分别分析各亚组内两种药物的效果。
当分组变量是一个连续性变量,例如年龄(岁),而不是年龄组,则需要人为将年龄离散化为年龄分组,才能进行亚组分析,而取什么年龄做为分割点(例如分为<18岁,≥18岁,还是<30, 30-60, ≥60岁),可能导致的亚组分析结果不同。取什么分割点主要和研究设计、指标选择等相关,一般可以采用学科共识、前人经验,临床约定,或者统计学里的曲线观察(例如交互作用RCS曲线、广义添加模型)等方式确定。而本模块则给用户提供了一个不同切割点进行亚组分析的测试平台,可以快速地得到不同切割点设置后的亚组分析结果。可以用于自己非正式测试,或者用于敏感性分析。
5.9.4 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.9.6 选择结局变量的类型
进入软件后,选择“回归分析”模块。
在“选择结局变量的类型”部分,根据您的研究需求,选择适合的回归模型:
二分类变量(Logistic回归,例如是否转移,是否客观缓解等)
连续性变量(线性回归,例如生物标志物值等)
生存变量(Cox回归,例如总生存期(OS),无进展生存期(PFS),无病生存期(DFS)等)
5.9.7 选择结局变量/应变量
根据您在第一步选择的结局变量类型,进行相应的操作:
Logistic回归:
系统会自动筛选数据库中所有的二分类变量。
在“请选择结局变量/应变量”下拉菜单中,选择您的结局变量。
线性回归:
系统会自动筛选数据库中所有的连续性变量。
在“请选择结局变量/应变量”下拉菜单中,选择您的结局变量。
Cox回归:
系统会自动筛选数据库中所有的连续性变量。
在“请选择代表时间的变量”下拉菜单中,选择表示时间的变量(如从开始到死亡的时间,或从开始到末次随访时间)。
系统会自动筛选数据库中所有的二分类变量。
在“请选择代表患者最终状态的变量”下拉菜单中,选择表示患者最终状态的变量(如1代表发生事件,0代表删失)。
5.9.8 选择结局变量的水平
Logistic回归和Cox回归:
系统会自动检测结局变量的所有水平。
在“请下拉选择结局变量的哪个水平表示发生事件”下拉菜单中,选择表示发生事件的水平(注意:选中的水平在建模时系统会设定为1,剩下的水平会设定为0)。

5.9.9 选择解释变量/自变量
在“要研究的解释变量/自变量的类型”部分,选择变量类型:
二分类变量
连续性变量
系统会根据您的选择筛选相应的变量。
在“请点击选择要研究的解释变量/自变量”下拉菜单中,选择您的解释变量/自变量。
5.9.10 选择参照组和观察/试验组(仅针对二分类解释变量)
系统会自动检测解释变量的所有水平。
在“请下拉选择参照组”下拉菜单中,选择参照组。
在“请下拉选择观察/试验组”下拉菜单中,选择观察/试验组。

5.10 自动筛选从单因素分析进入多因素分析的变量(逐步回归/最优子集/Lasso/岭回归/弹性网络/随机森林/Boruta法)
本指南介绍 自动变量筛选 模块的原理与使用方法,帮助你在进入正式的多因素建模前,从候选自变量中高效筛选出一组稳定、可解释、可复现的变量组合。
主要特点:
根据上传的科研数据,简单点击设置后,全自动完成从单因素到多因素的变量筛选
支持一般线性回归、Logistic回归、Cox回归、Poisson回归
支持穷举最优子集、逐步 AIC 回归、Lasso、岭回归、弹性网络、随机森林、Boruta 等方法
自动作图,自动给出图表,生成单因素和多因素分析可供投稿的最终图表结果。
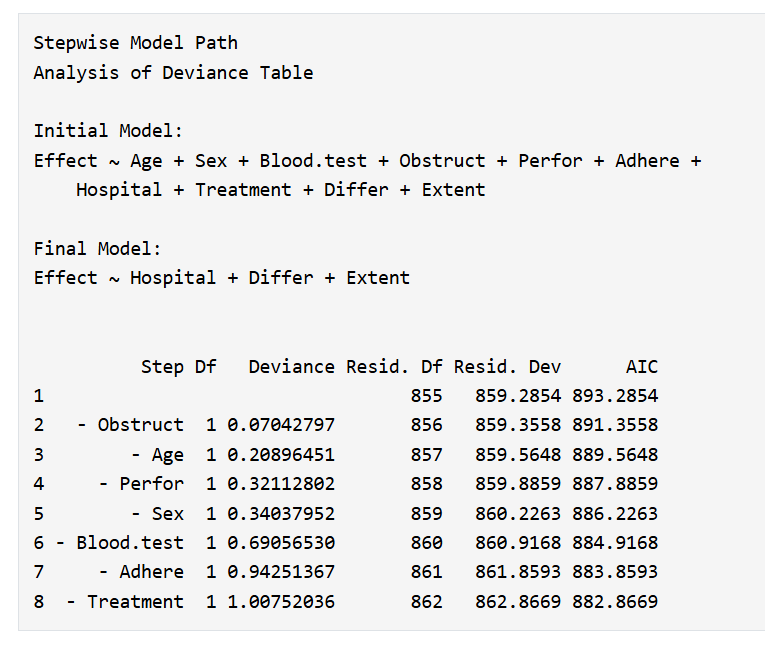
AIC 逐步回归
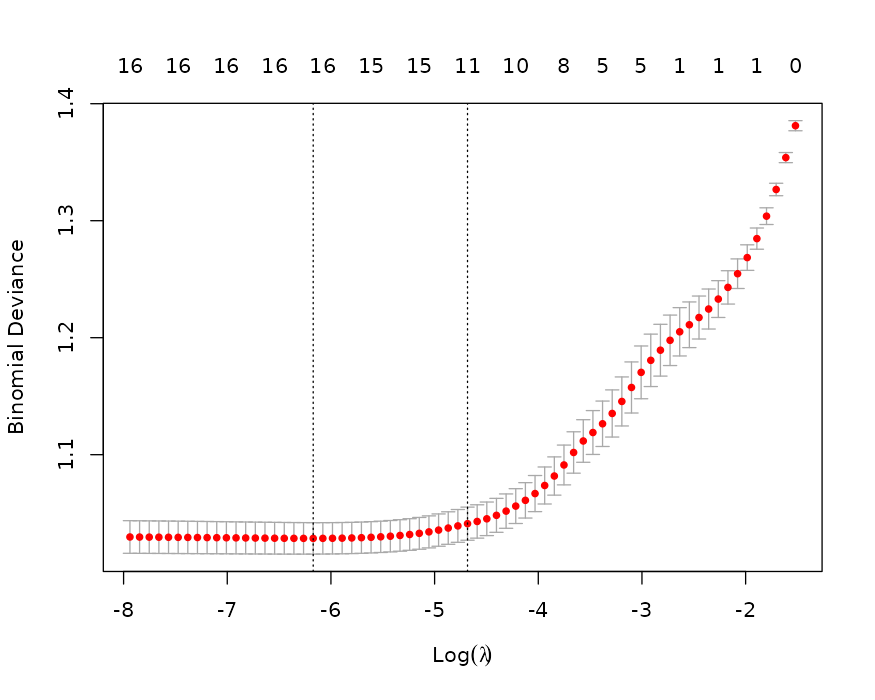
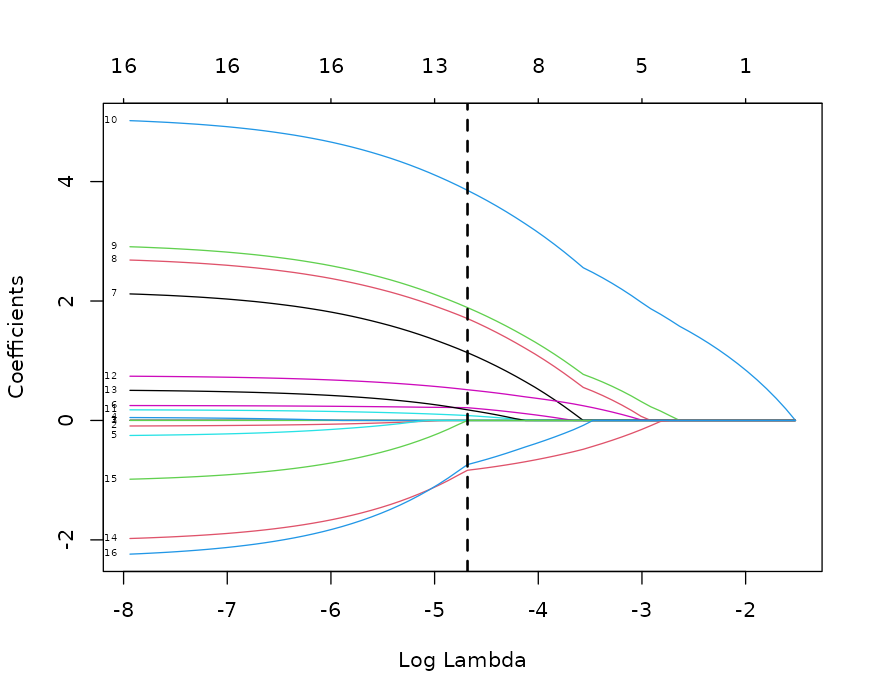
Lasso、Ridge、Elastic Net
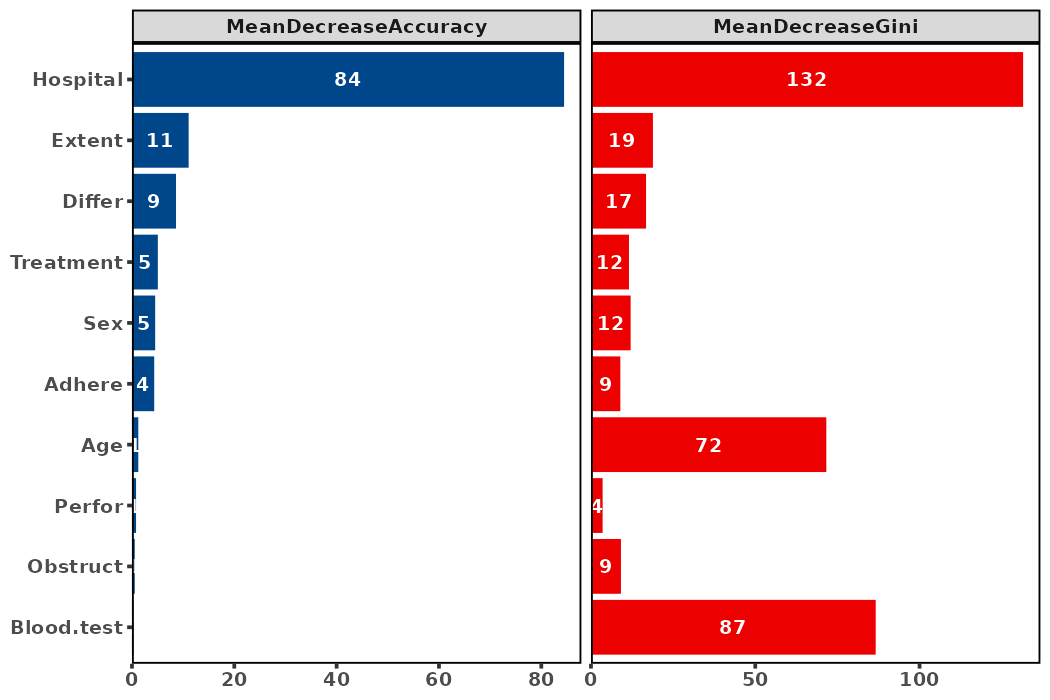
随机森林 SHAP
Boruta
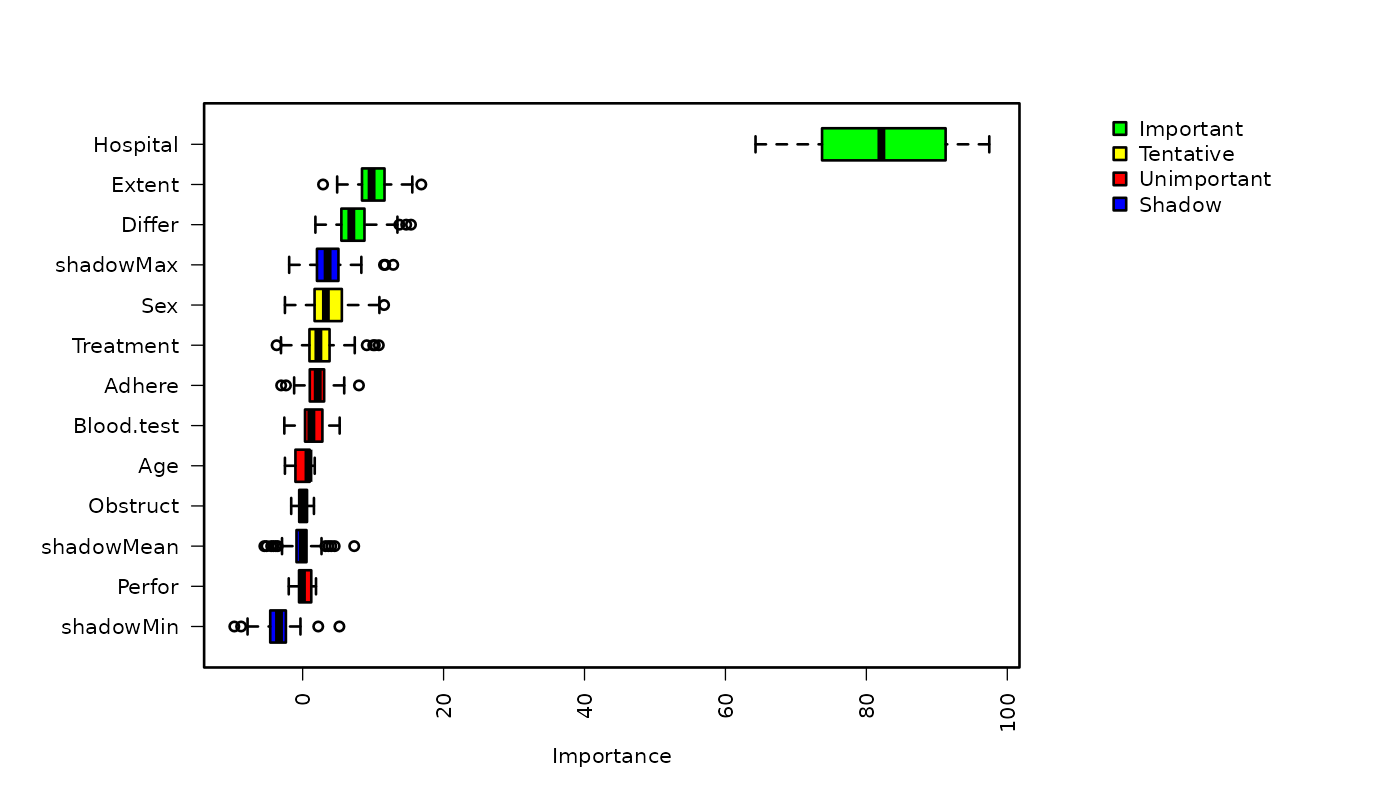
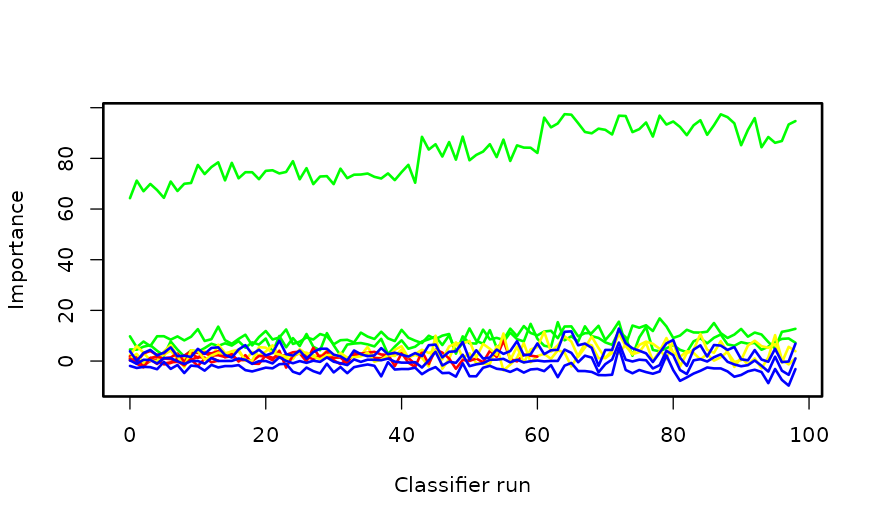
5.10.1 背景与定义
5.10.1.1 什么是变量筛选(Feature/Variable Selection)
变量筛选指在既定的结局(应变量)与候选自变量集合中,通过统计学或机器学习方法,选出对模型预测或解释最有价值的一组变量,以提高模型稳定性、泛化能力,并降低多重共线性与过拟合风险。
常见动机:
- 解释/因果:在控制混杂的前提下,得到更稳健的效应估计(OR/HR/Beta 等)。
- 预测/建模:提升泛化性能,减少冗余特征,提高计算效率。
- 展示/发表:在结果表中保留更有意义、更易解释的一组变量。
5.10.1.2 方法速览与取舍
- 逐步回归(AIC 导向,MASS::
stepAIC):以 AIC 最小为准选择模型,便于叙述与复现;- 提醒:不推荐以 P 值阈值(如 P<0.1)作为筛选规则——这是过时做法,为之前的主流,大量见于旧的统计教材和前些年的论文,但已经得不到目前世界主流统计学家的认可,易导致偏误;本模块不采用 p 值来筛选变量,采用 AIC/BIC 等信息准则。
- 最优子集(Best Subsets):穷举或近似穷举寻找若干优选模型,计算量大;本模块目前暂停此功能以保护服务器资源。
- 正则化(Lasso / Ridge / Elastic Net):
- Lasso(α=1):可将部分系数压缩为 0 → 自动筛选变量;
- Ridge(α=0):系数不会为 0,不自动筛选,但可缓解共线性;
- Elastic Net(α在0到1之间):可取0.5,表示 L1+L2 折中,适合存在组相关性的特征。
- 随机森林变量重要性(VIP):
- 分类(如 Logistic):常见重要性指标 MeanDecreaseAccuracy/MeanDecreaseGini;
- 回归(如 线性/Poisson):常见重要性指标 %IncMSE/IncNodePurity;
- 生存(Cox,
randomForestSRC):使用 VIMP 指标。
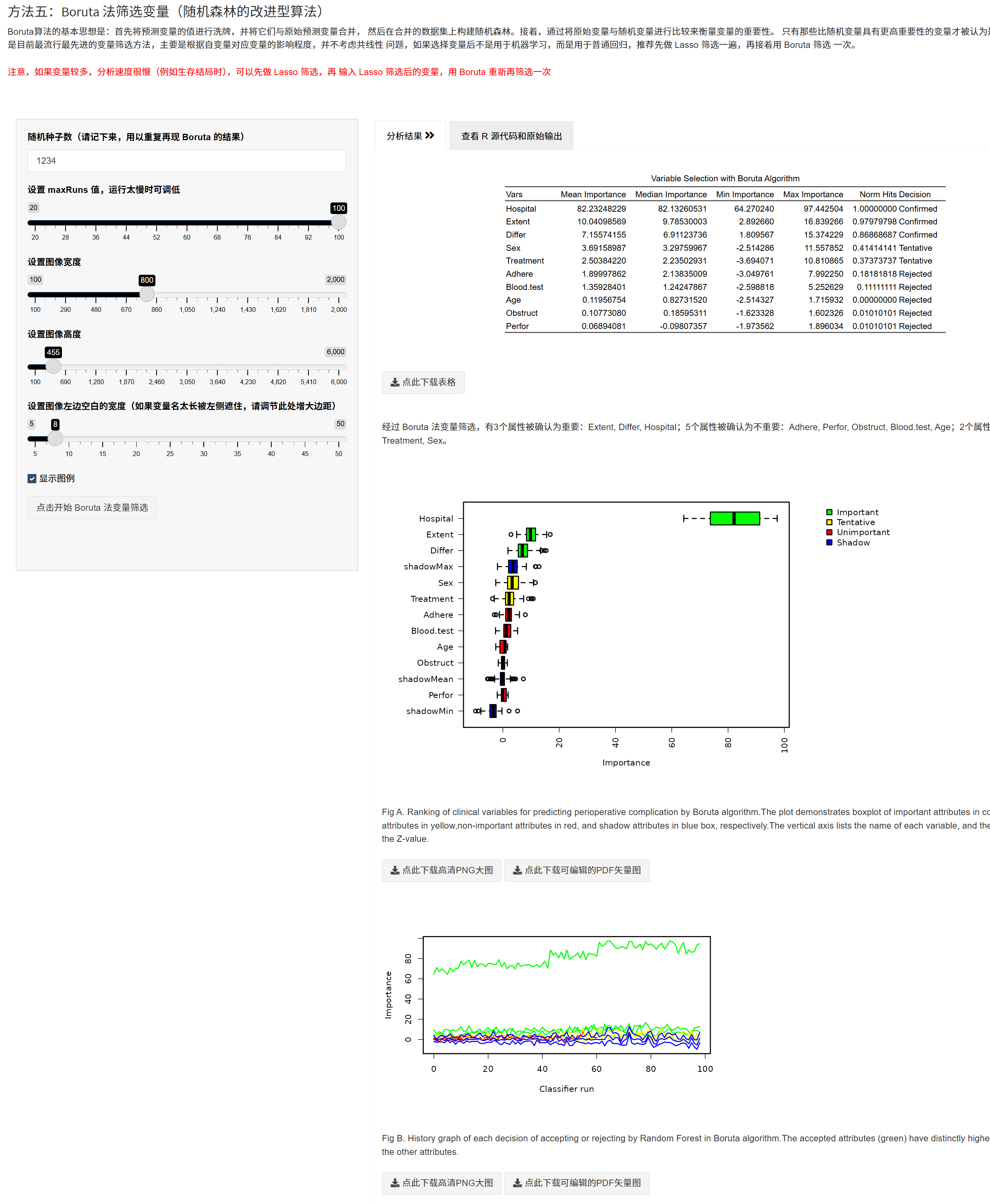
- Boruta(VIP):相对“伪造特征(shadow)”的稳健重要性检验,能识别非线性/交互贡献;高维时建议先 Lasso 再 Boruta,以提升效率。
实践建议:若候选变量 >50–100(甚至上百),建议跳过单因素与逐步回归,先用 Boruta 初筛,再结合 Lasso/专业知识做二次筛选。
5.10.2 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.10.3 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“自动筛选从单因素分析进入多因素分析的变量(逐步回归/最优子集/Lasso/岭回归/弹性网络/随机森林/Boruta法)” 进入模块:

5.10.4 设置结局类型与变量(必做)
左侧依次完成:
- 选择结局类型(family):
- 二分类(Logistic)、连续(线性)、生存(Cox)、计数(Poisson)。
- 选择结局(Y):
- Logistic:选择二分类变量,并在“事件水平”中慎选为 1;
- 线性:选择数值且去重>2的连续变量;
- Cox:选择 time(非负数值) 与 status(仅两类),并指定 status 的事件水平=1;
- Poisson:选择非负整数的计数变量。
- 选择候选自变量(X,多选,至少 2 个):系统会排除高基数(>30 水平)的因子,以及已选的 Y/time/status。
- 设置 95%CI 计算方法(影响后续所有回归表):
- Wald CI(与 SPSS/STATA 一致;
confint.default()); - Profile likelihood CI(R 更精确;
confint();极端情况下与 Wald P 值略有不一致,可优先报道 CI)。
- Wald CI(与 SPSS/STATA 一致;
- 点击 “生成下一步所需的数据集”:生成并预览 “原始数据概览” 与 “剔除缺失值后数据”。
排错清单(强烈建议在此步完成):若 Logistic/Cox/Poisson 里出现 OR/HR/RR=0、Inf、或极端大值,请: 1) 检查是否将同一信息以不同形式同时作为 Y 与 X(如年龄与年龄分组); 2) 合并事件全无/全有或样本极少的类别水平; 3) 处理缺失(建议删除缺失>20%的变量或先做填补)。
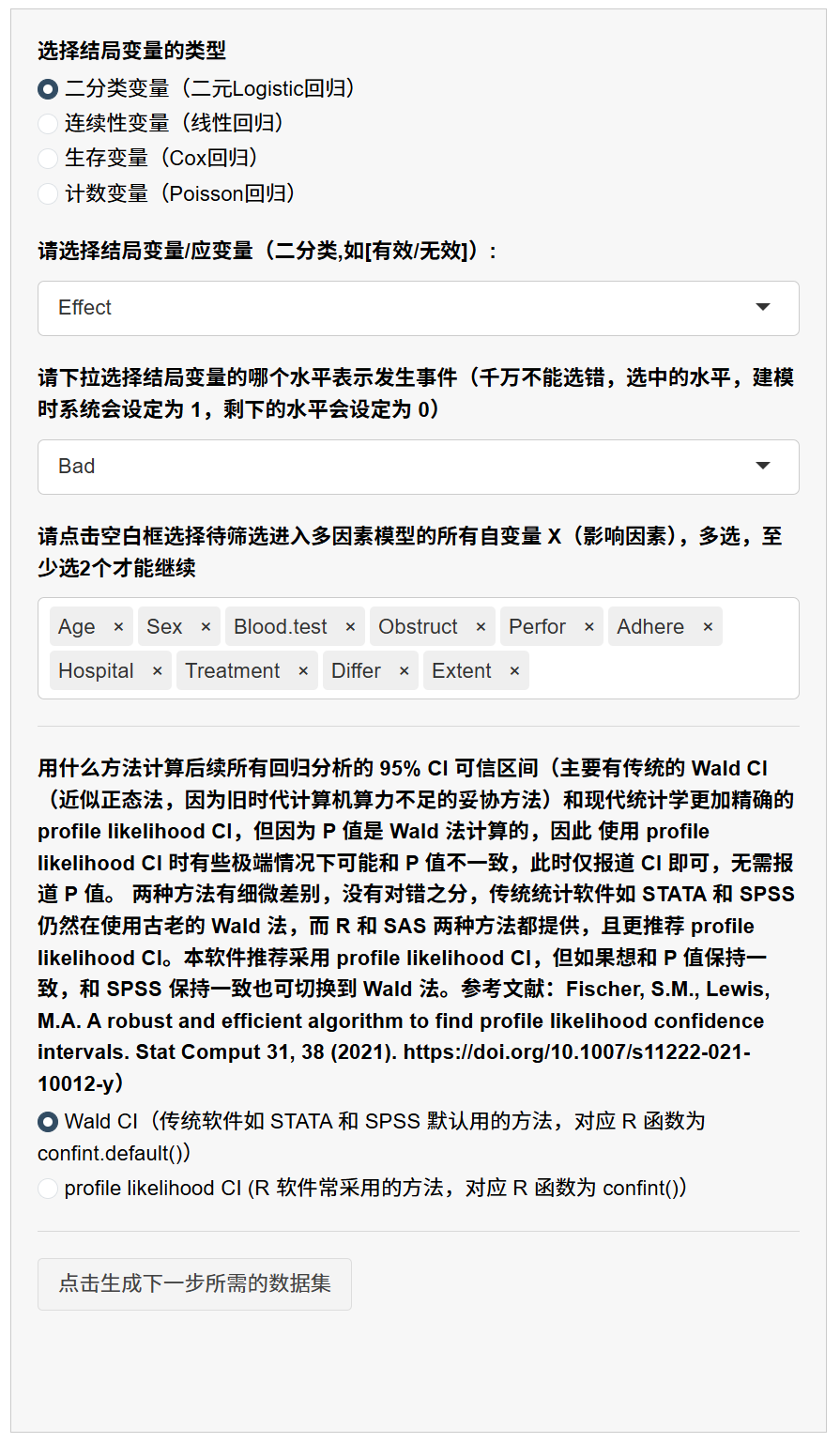
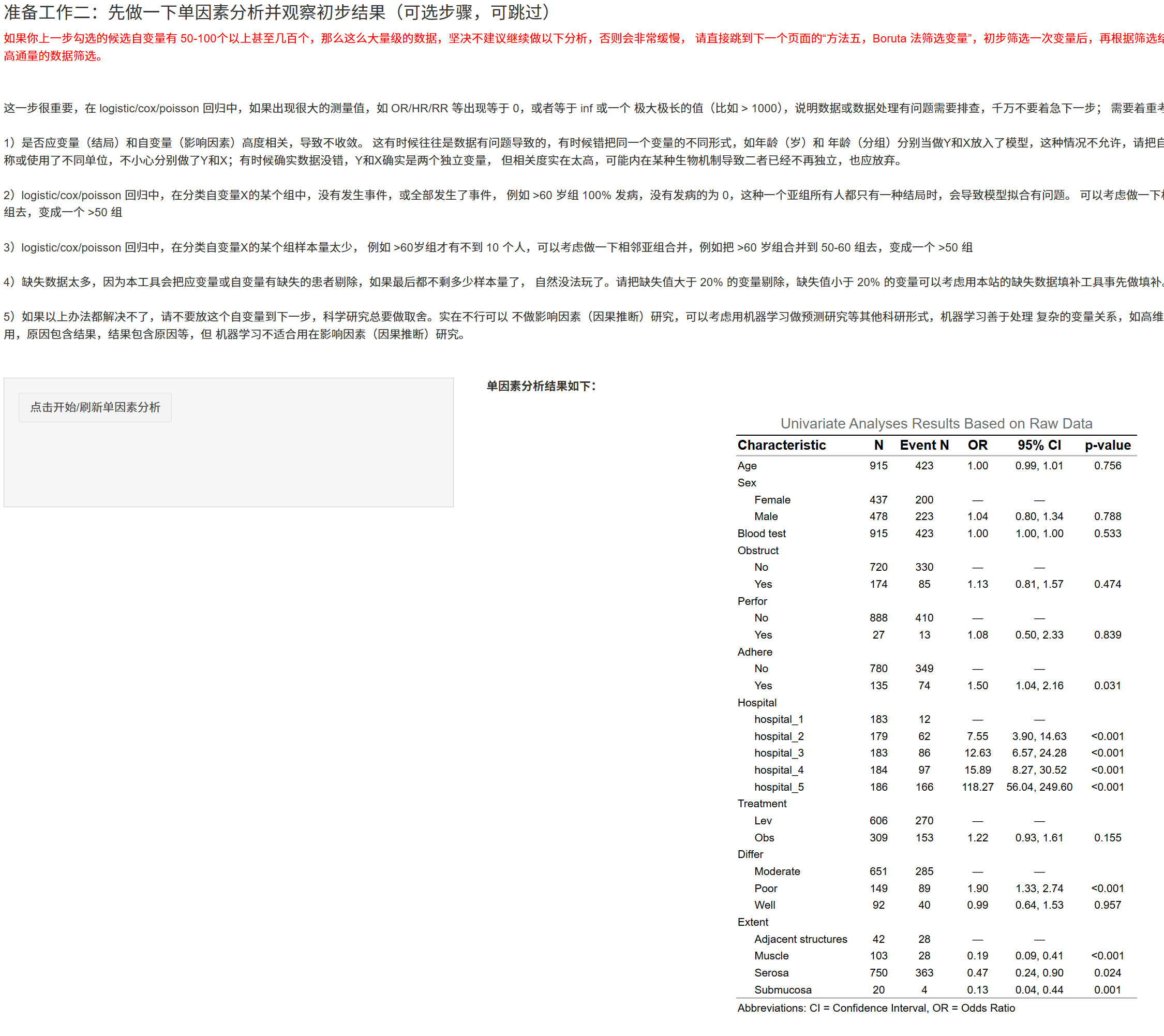
5.10.5 单因素分析(可选)
点击 “开始/刷新单因素分析”,系统使用 gtsummary::tbl_uvregression 逐一评估每个 X 与 Y 的关系(仅单因素)。 - Logistic/Cox/Poisson 输出 OR/HR/RR 与 95%CI,并显示 N/事件数; - 适合做快速体检,识别分离问题与异常值,但请勿将其与多因素结果比较。
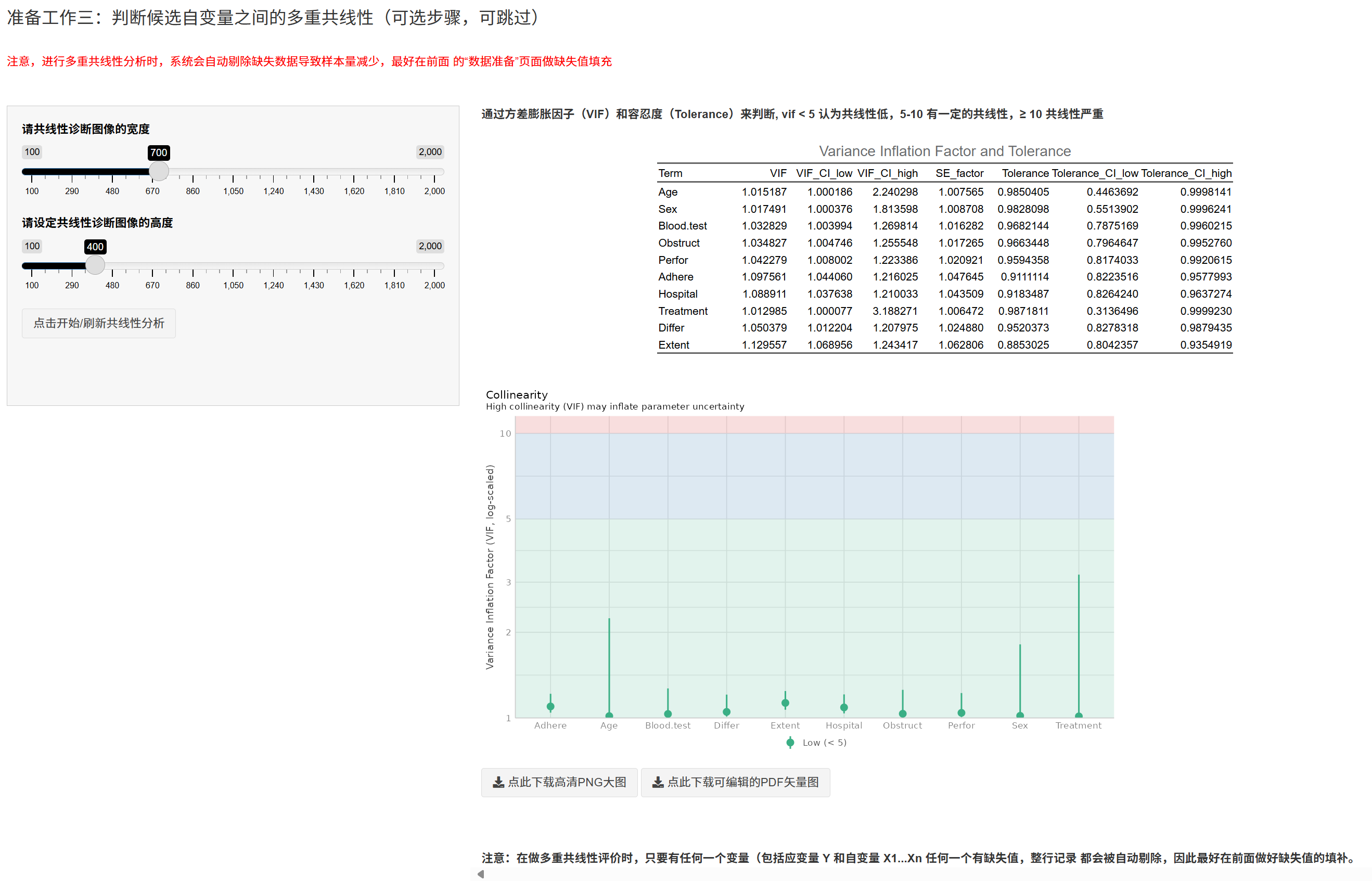
5.10.6 多重共线性诊断(可选)
点击 “开始/刷新共线性分析”,返回 VIF/Tolerance 与诊断图(performance::check_collinearity)。 - 经验阈值:vif < 5(较低),5–10(一定共线性),≥10(严重); - 此步会整行剔除缺失,建议在“数据准备”先完成缺失填补。
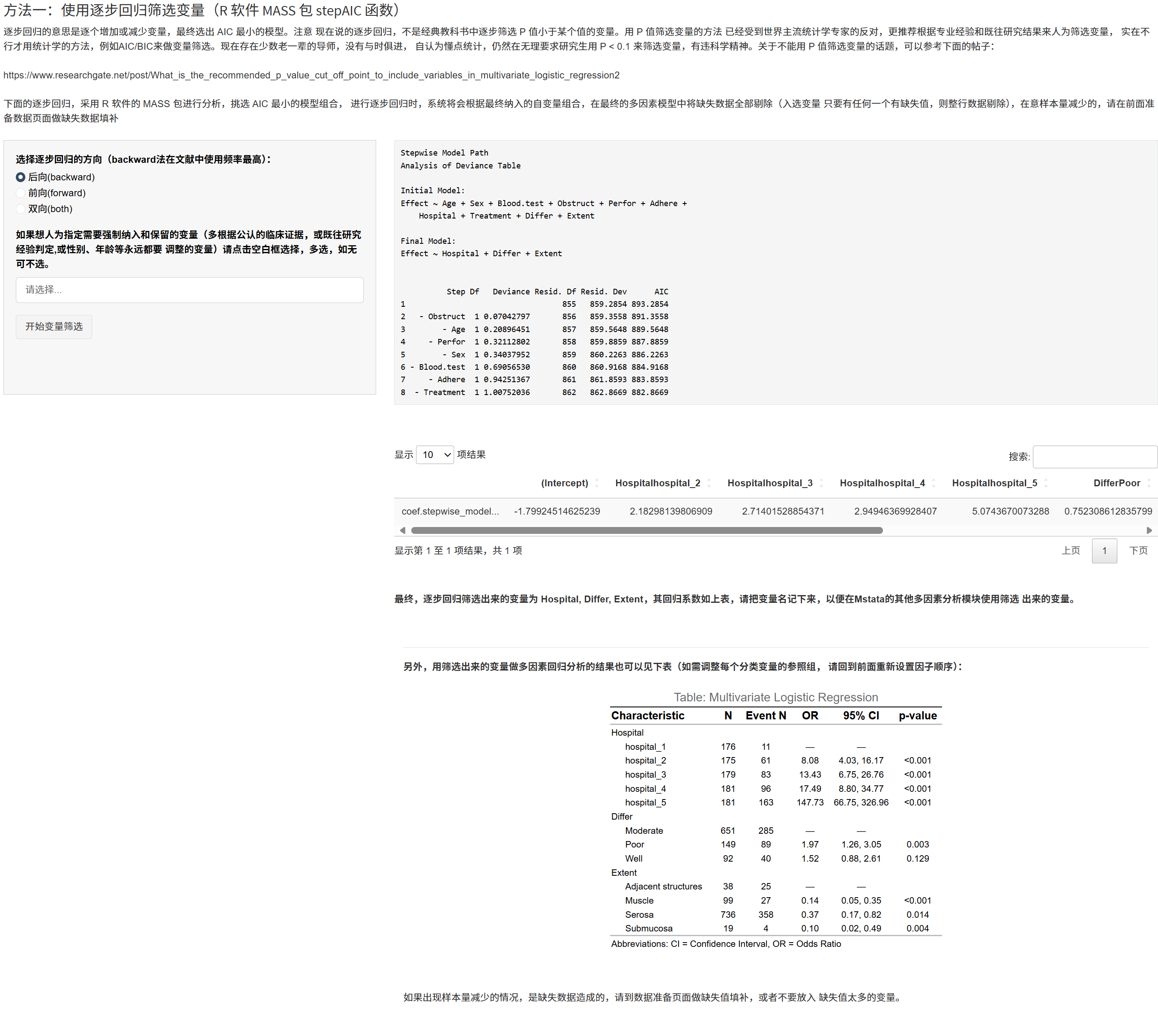
5.10.7 多因素变量筛选(核心)
5.10.7.1 逐步回归(AIC,MASS::stepAIC)
思路:以 AIC 最小为目标,按 后向 / 前向 / 双向 路径搜索模型。
设置: - 方向:后向(backward)(文献中使用最广)、前向(forward)、双向(both); - 强制纳入变量:常用于公认混杂因子(如年龄、性别等); - 双向时的起始模型:可指定起始变量集(需包含强制变量)。
运行:点击 “开始变量筛选”。
输出: - 逐步过程表(ANOVA 风格)与最终系数表; - 最终入选变量清单(请记下变量名,便于去到其他模块复用); - 使用入选变量回代原始回归模型的 gtsummary 表(可在前面“定义字段”调整因子参照组后重算)。
下载:支持 Word(.docx)导出。
注:逐步回归以 AIC 而非 P 值阈值作为准则,更符合当前共识;若样本量对缺失较敏感,可先在“数据准备”做缺失填补。
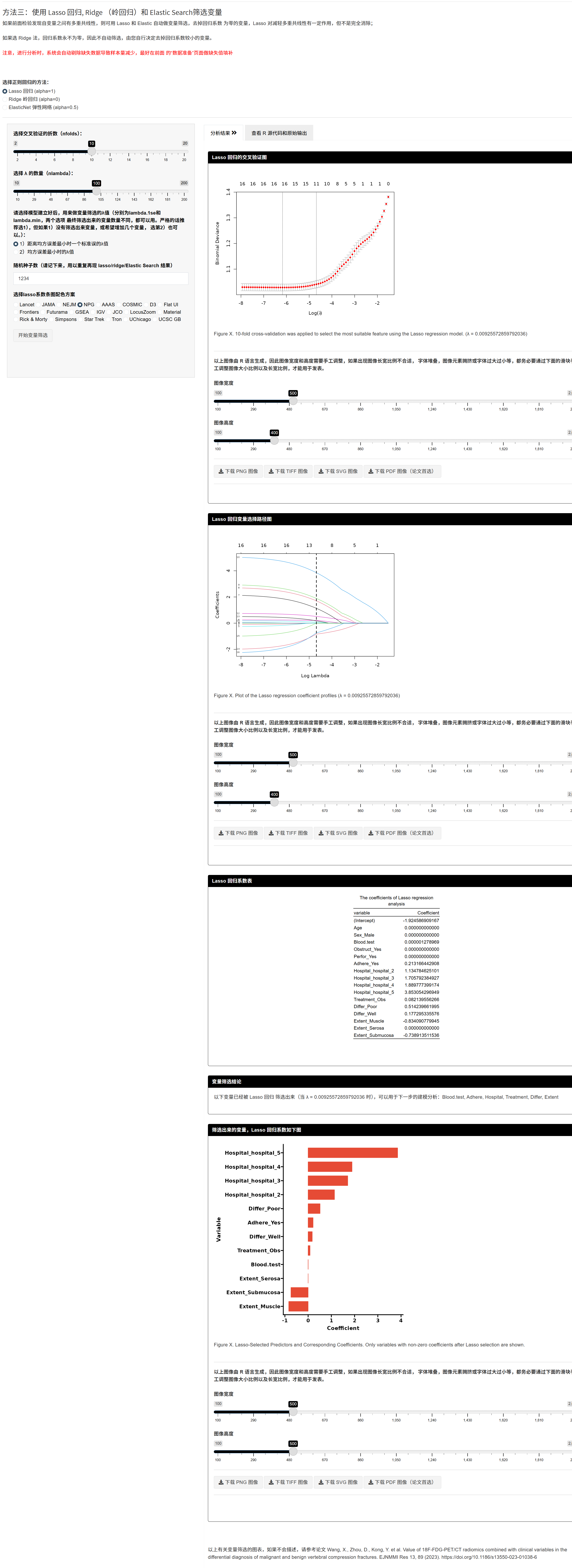
5.10.7.3 正则化(Lasso / Ridge / Elastic Net)
选择方法: - Lasso(α=1):自动筛选(系数可为 0),缓解共线性; - Elastic Net(α=0.5):兼顾 L1/L2,适合组相关特征; - Ridge(α=0):仅收缩,不筛选(系数不为 0)。
运行:在“选择正则回归的方法”中选择算法并开始;
结果解释: - 非零系数的变量即入选变量; - 模块会用入选变量回代至原始(非正则)回归并输出 gtsummary 表,便于期刊解释; - 需要可在“定义字段”中调整分类变量参照组后再重跑。
下载:支持 Word(.docx)导出。
小贴士:若变量很多或共线性明显,先用 Lasso 可以显著提速并稳定后续分析;Ridge 仅用于稳定估计,不做自动筛选。
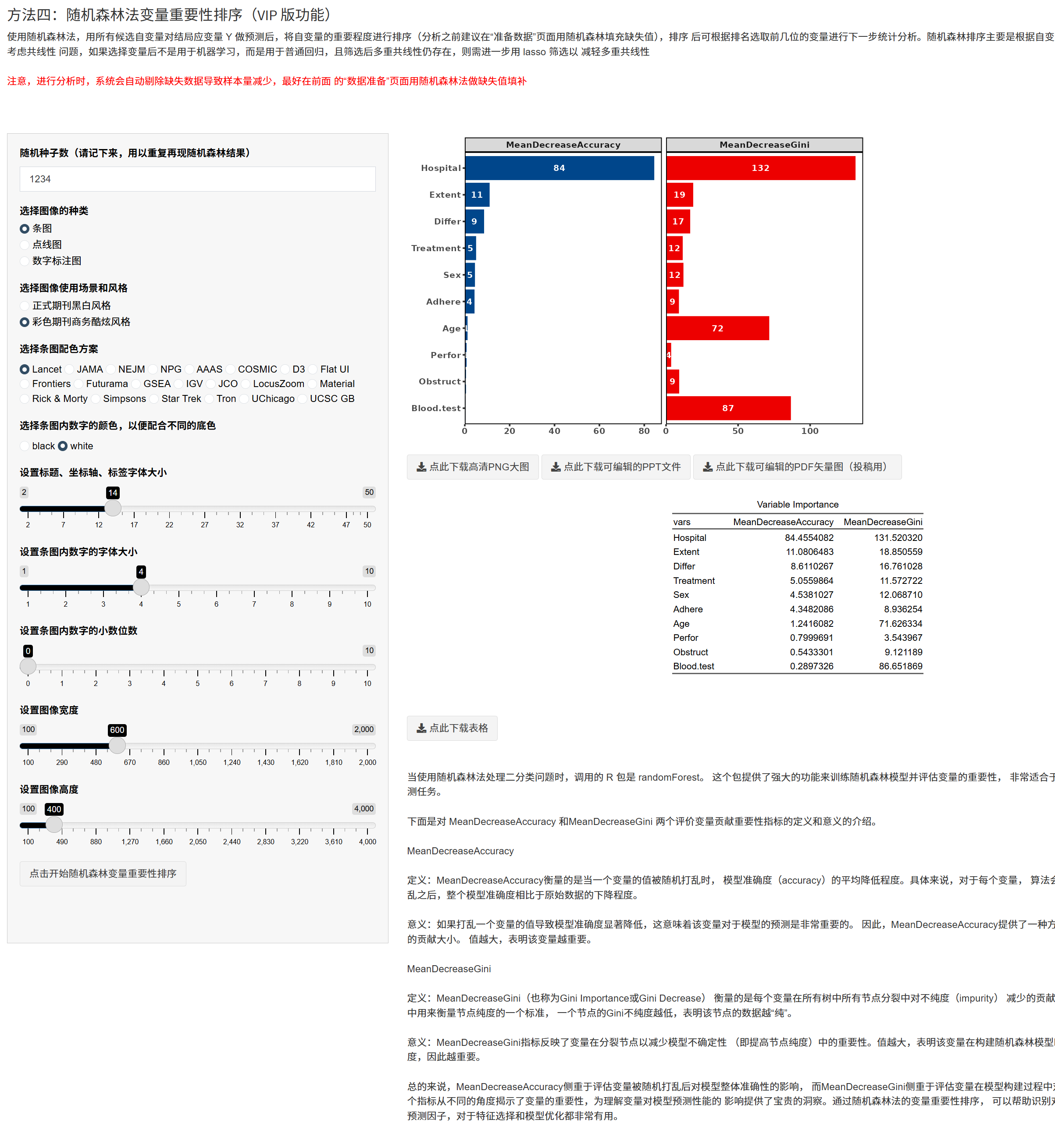
5.10.7.4 随机森林变量重要性(SHAP)
思路:用随机森林对结局进行预测,依据模型对每个自变量的重要性排序; - Logistic/分类:关注 MeanDecreaseAccuracy / MeanDecreaseGini; - 线性/Poisson 回归:关注 %IncMSE / IncNodePurity; - Cox 生存:randomForestSRC 的 VIMP 指标。
主要设置: - 随机种子(请记录以复现); - 图像风格:条图/点线图/数字图; - 期刊风格:黑白(simple)/彩色(color),并可选择多种期刊配色方案; - 数字颜色/字号、小数位、画布大小等; - 点击 “随机森林变量重要性排序” 开始。
输出: - 可发布的重要性排序图与表格; - 图表与表格均支持下载(Word 与高分辨率图片)。
建议:若你将筛选结果用于传统回归而非机器学习,随机森林不考虑共线性,排序后可再用 Lasso 做二次筛选以减轻共线性。
5.10.8 导出与复现
- 表格均支持 Word(.docx) 下载;图形支持 PNG/PDF 下载。
- 首次生成或刷新图表后,建议等待 10–15 秒再点击下载,避免下载到旧文件(下载后也请对照页面核对)。
- 记录:随机种子、最终入选变量名单与模型设定,以保证结果的可复现与可溯源。
5.11 阈值效应和 sengmented / piecewise 分段/断点回归
在医学和流行病学等领域,研究者常常关注某个连续性自变量(例如年龄、BMI、血糖、血压、某生化指标等)与结局变量之间是否存在“阈值效应”或“拐点”。若真的存在这样一个或多个临界点,自变量在不同区间对结局的影响强度(斜率)往往并不相同。此时,传统的线性假设可能会低估或忽视这种非线性变化,难以准确反映真实的生物学机制。
分段回归(Piecewise Regression,也称为“分段线性回归”或“分段广义线性回归”)正是为应对上述情形而设计的一种分析方法。它允许研究者在一个或多个拐点处人为(或自动)地将连续自变量拆分为若干区段,然后在每个区段内假设自变量与结局之间呈线性关系,从而更清晰地捕捉到潜在的拐点或阈值效应。
下文将从以下几个方面介绍分段回归的方法、应用场景、操作流程以及软件实现细节。
| Piecewise 线性回归 | Piecewise Cox 回归 | Piecewise Poisson 回归 |
|---|---|---|
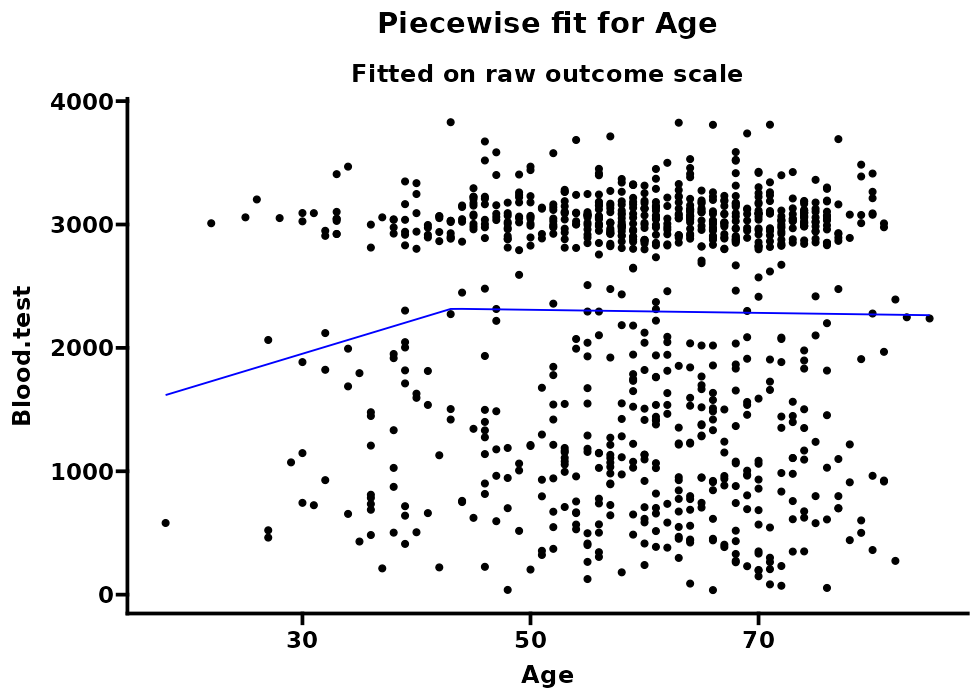 |
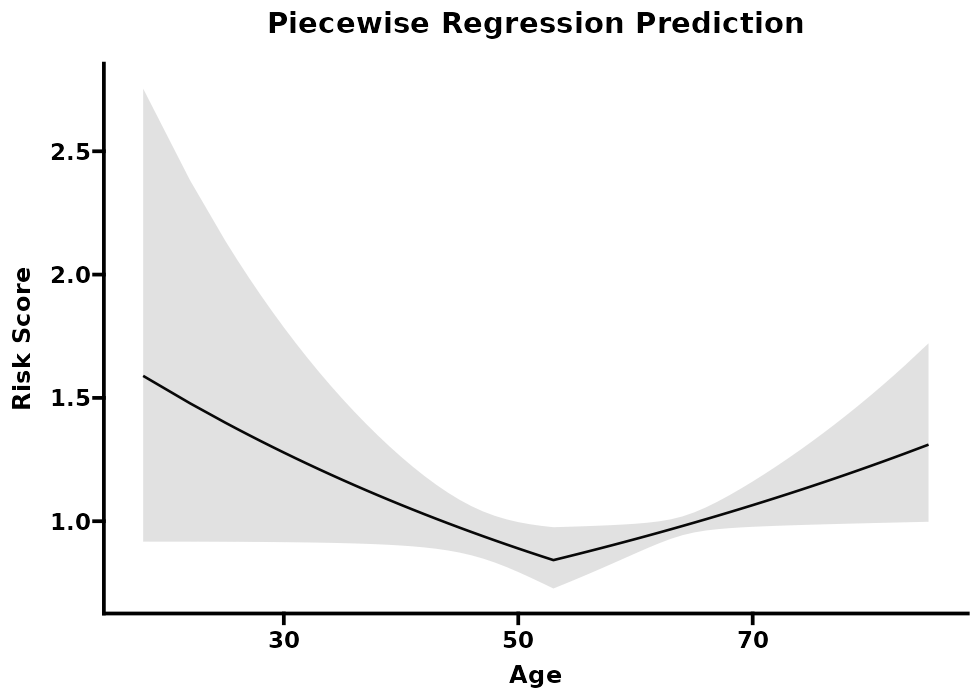 |
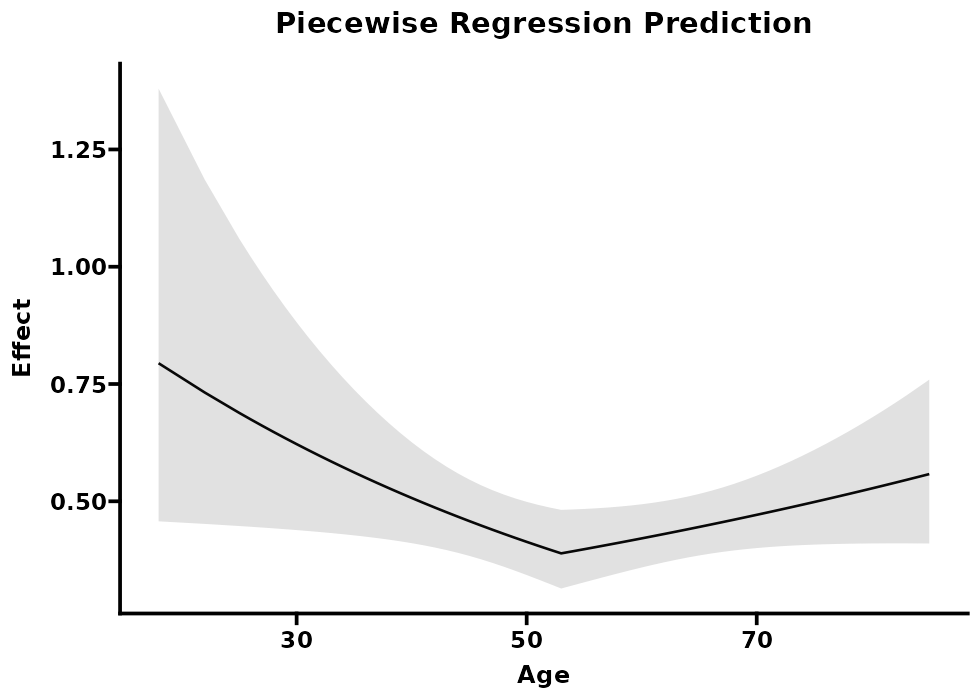 |

5.11.1 基本思想
在医学研究中,当我们怀疑某生理指标(例如血压、血糖或 BMI)过低或过高都可能导致不良结局时,则可考虑使用分段回归(Piecewise Regression)来刻画这种潜在的“U 型”或“J 型”关系。

这种做法让我们能够分别估计 X 在不同区间对 Y 的影响斜率,从而精准捕捉到在拐点处风险或效应发生转折的现象。
5.11.2 常见的应用场景
阈值或临床拐点探索
例如,血压或血糖若高过某一点会急剧增加心血管事件风险;也可能在过低时对某些人群不利。通过分段回归,可准确定位该“临界值”。剂量-反应或剂量-毒性研究
药物剂量与疗效/毒性的关系可能在特定区间内线性增加,但超过某个阈值后毒副作用会显著提升。分段回归有助于找出合理的剂量范围。生物学上明显分区间的指标
某些指标如 BMI、某些激素水平、实验室指标等,往往有文献或先验信息提示潜在的“安全区间”。使用分段回归能将这些先验的区间或阈值纳入定量模型中。替代无脑分组
以往研究中常将连续变量简单地分为“高、中、低”三组进行卡方检验或Log-rank 检验,这样容易损失信息。分段回归则在不随意多级分组的前提下,灵活又有 interpretability。
5.11.3 与其他方法的对比
与线性回归相比
分段回归更能捕捉不同区间的差异,适合怀疑有明显阈值的情形;若根本不存在拐点或非线性,分段回归就不会比简单的线性回归更有优势,且增加了模型复杂度。与多项式回归、样条回归相比
多项式回归或样条回归(如限制性立方样条 RCS)在对连续变量进行拟合时较平滑,能在整体上刻画更复杂的曲线形状。
分段回归则更强调“在拐点之前是一种趋势,拐点之后换另一种趋势”,并且在拐点处会有比较明显的线性拼接。对于某些存在“阈值”或“转折”概念的研究更直观。
5.11.4 分段回归在医学科研中的优势
能够更直观地解释阈值效应
一旦在模型中估计出ψ等拐点位置,就可清晰指出“某一数值是转折点”,并量化其在不同区间的斜率或风险比。减少信息损耗
与将连续变量硬性分组相比(如三组或四组),分段回归最大程度保留了连续信息,只是在可能出现转折的地方做局部处理。便于个体化指导
如果在 BMI、血糖或血压的分段回归中发现了确切的高风险段,临床上就可以根据该阈值更精准地干预或随访。可辅助其他统计方法或生物学假说
分段回归的结果也能与线性回归、Loess 平滑、甚至是样条回归的结果进行对比验证。若各方法都发现同样的转折点或阈值,就能更有信心地发表或应用。
5.11.5 常见的分段回归类型
在广义线性模型(GLM)框架下,几乎所有常用的回归都可做“分段”处理,只要我们将自变量增加一个或多个“截断”函数即可:
Piecewise 线性回归
适用于连续型结局。示例:研究实验室某连续指标(如血清酶浓度)随温度或时间的转折关系。Piecewise Logistic 回归
适用于二分类结局(如疾病发生与否、疗效好坏)。示例:将某炎症指标作为连续自变量,检验其在不同区段时对二分类结局的 OR 是否明显变化。Piecewise Cox 回归
适用于生存数据(需 time 和 status 两个变量),常用于找出生存风险在不同区间的变化。示例:年龄在某个区段内对死亡风险的影响相对平稳,但超过一定岁数时风险陡增。Piecewise Poisson / Quasipoisson 回归
适用于计数型数据(如某项事件的发生次数),检验在某个区间后是否出现跳变或陡增趋势。
5.11.6 自动或手动确定拐点
5.11.7 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.11.9 进入“阈值效应和 piecewise 回归”界面

在软件左侧或顶部标签栏找到“阈值效应和 piecewise 回归”Tab。
该界面通常分为左侧侧边栏和右侧主显示区两部分:
侧边栏:包含模型类型、结局变量选择、自变量选择、协变量选择、以及“Piecewise 回归设置”等输入控件。
主显示区:在您点击“生成/更新 piecewise 回归分析结果”后,右侧会显示分段回归的表格结果与图形。

5.11.10 选择回归类型与变量
在侧边栏的“模型设置”区域:
回归类型(family)
例如:二分类结局选 Logistic 回归(OR)或 Poisson/Quasipoisson 回归(RR);生存分析选 Cox 回归(HR);计数结局则选 Poisson/Quasipoisson(RR),等等。
您只需按照自己研究的结局类型选择对应的方法即可。
选择结局变量
Logistic 回归:指定二分类变量,并选择哪个水平代表“事件=1”;
Logistic 回归:指定二分类变量,并选择哪个水平代表“事件=1”;
Cox 回归:指定 time 和 status;
Poisson / Quasipoisson:指定一个非负整数的计数变量;
Linear 回归:指定一个连续型结局等等。
选择自变量(predictor)
- 即在图中和模型中将做分段的“连续变量”。若下拉菜单找不到某变量,可能是它未被设置为 numeric(在“数据准备”模块中可切换变量类型)。
选择协变量(covariates)
- 若需做多因素调整,可在此多选一个或多个;若不需调整协变量,可留空。
5.11.11 选择分段回归方法
在侧边栏下方“Piecewise 回归设置”区域中,您将看到以下三个选项,可根据研究需要任选其一:
自动寻找折点(
segmented包)(A)“设置折点数量(npsi)自动搜索”
- 例如 npsi=1 即寻找 1 个折点,将自变量分成 2 段;若怀疑有 2 个拐点,可设 npsi=2,以此类推。
(B)“指定一个折点起始值(psi)再自动搜索”
- 当对折点大致所在范围已有先验认识时,可输入一个起始数值,软件将从此数值附近开始迭代搜索最优折点。
该方法基于 R 包
segmented的迭代算法,可给出最优的折点位置及对应区段的回归系数与显著性。
人为指定折点(固定值)
直接手动输入折点,如“43”,或多个折点用英文逗号分隔,如“43, 60”。
适用于已有较多文献或临床先验信息,或从其它方法(如可视化)已清晰识别到具体的拐点位置。
提示:如果对拐点所在位置完全没有想法,可先尝试自动搜索模式;若搜索到的折点有明确临床意义,也可在后续分析中将其作为“固定折点”写入论文。
5.11.12 其他选项设置
保留小数位数:可调节效应量(OR/HR/RR/Coefficient)和 P 值的小数位,以满足期刊格式要求(常见:OR/HR/RR 保留 2~3 位小数)。
图像尺寸:可调节宽度和高度,使结果图在网页预览或下载时适配不同的大小。
5.11.13 生成和查看结果
点击“生成/更新 piecewise 回归分析结果”
软件将自动执行后端运算,完成分段回归的拟合。
若选择自动搜索折点方式,软件会输出搜索到的最佳折点位置。
右侧主显示区
将显示一份分段回归表格,列示各区段的回归系数(或 OR/HR/RR 及其 95% CI)与相应的 P 值等统计信息。
同时会生成一张可视化的分段曲线图(针对可绘制出拟合线的情况,例如线性回归,或用特定可视化方式展现 Cox/Logistic 之分段结果),并在图中标出折点位置。
结果解读要点:
折点:在输出的表格里若看到“Break-points = 42.7”之类,说明自变量在值为 42.7 附近时出现明显的风险转折。
各区段斜率/效应量:表中会显示不同区间内自变量与结局的关联强度;例如区间 1(X < 42.7)时 OR=1.02,区间 2(X ≥ 42.7)时 OR=1.10,暗示在第二区段中自变量单位变化对结局的影响更大。
5.11.14 下载 Word 报告
在“下载 word 报告”页面:
点击“点此下载 word 文档”按钮,软件会自动打包当前 piecewise 分段回归的结果、模型参数表格、方法学描述等,形成一份可读性较好的 Word 文件。
Word 文件可在后续论文写作或组内讨论时直接引用;请用微软 Word 打开,避免在 WPS 等软件中出现格式错乱。
5.11.15 查看/下载原始输出和 R 源代码
在“查看 R 源代码和原始输出”页面:
可以一键下载当前分析所使用的
dt.RData数据集。可以查看或下载自动生成的 R 代码与回归输出,以便您或审稿人复现结果。
若您不熟悉 R 语言,可忽略此步骤;软件已在后台帮您完成这些运算。
5.11.16 常见问题与注意事项
折点数量过多
- 理论上可设置多个折点,但在医学研究中,通常只考虑 1~2 个拐点。拐点过多不仅会使模型复杂、解释困难,还可能导致过拟合。
自动搜索到的折点无临床意义
- 当自动搜索到的折点不符合生理或临床常识时,需谨慎解释。可以再尝试人工指定或者进一步核对数据分布。统计结果必须与临床背景相结合。
分段回归 vs. 亚组分析
分段回归是将“连续变量”在同一个模型中通过截断函数进行分段,区段之间是拼接且连续的;
亚组分析通常是把人群完全拆分为“不同子人群”后做平行分析,其方法学与分段回归不同,得到的结果也不可简单等同。
拐点与线性假设
- 当无显著非线性或模型诊断认为折点不必要时,完全可以回到简单线性回归 / Cox / Logistic 模型。
数据分布极端不平衡
- 若某段区间样本数极少,会导致估计不稳定,置信区间极宽或无法收敛。建议保证各区间有足够样本量。
5.11.17 总结
分段回归(Piecewise Regression)在医学与流行病学研究中具有重要应用价值,尤其适用于发现和量化自变量在某些关键阈值或转折点前后的差异性影响。本软件在“阈值效应和 piecewise 回归”模块中,为用户提供了易于操作的一站式分段分析功能,包括:
自动 / 人工确定折点
多种回归类型(Logistic、Cox、Poisson 等)适配
分段结果与可视化图形自动生成
一键导出报告和R 源代码以便复现
通过以上功能,研究者无需自行编写复杂的统计脚本,即可高效完成对连续变量的阈值探索与分段拟合,并在论文和报告中直观呈现各段的回归系数、P 值以及折点位置,从而为临床诊疗和公共卫生决策提供更精准的证据。
5.12 限制性立方样条图 RCS
限制性立方样条(Restricted Cubic Splines, RCS) 是一种在回归模型中用于处理非线性关系的灵活方法。传统的线性回归往往假设自变量和因变量呈单调直线关系,这在实际研究中可能过于简化,无法准确捕捉真实的非线性变化。而 RCS 则通过在自变量的取值范围内设置若干个“节点”(knots),将一系列三次多项式片段拼接成一条平滑、连续的曲线,从而更精确地反映出自变量与结局变量可能存在的复杂关系。
| 线性均匀尺度 | 对数尺度 | 伪对数尺度 | |
|---|---|---|---|
| OR值 | 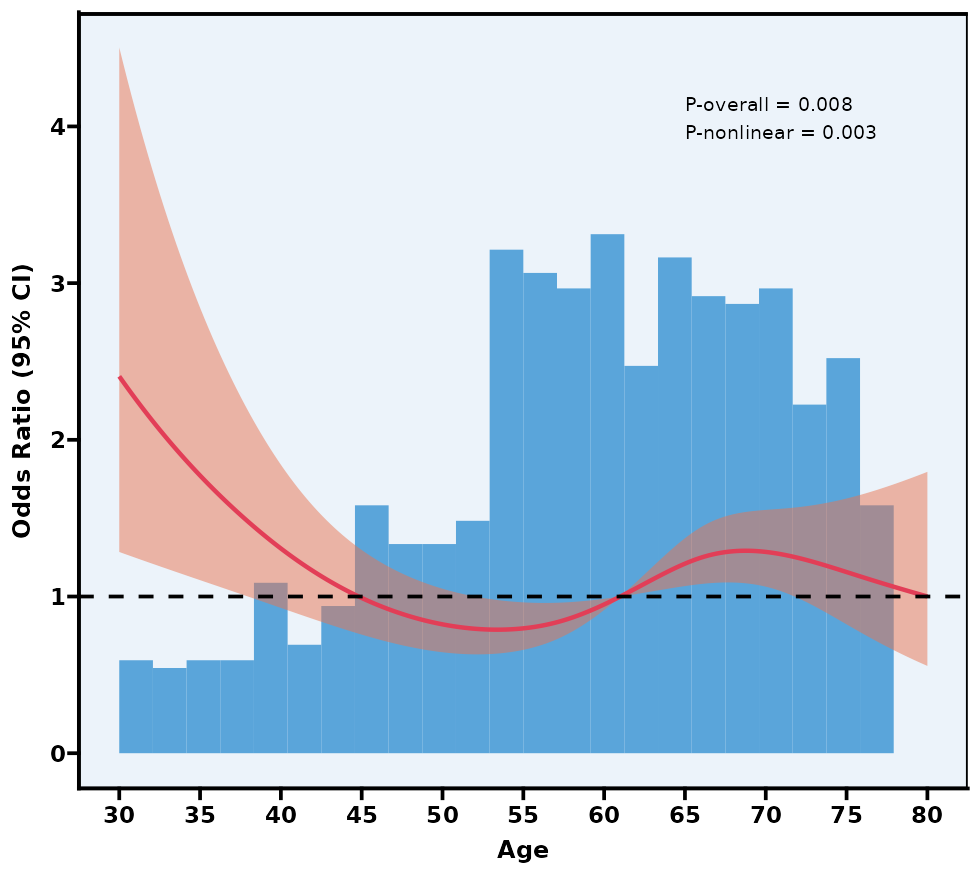 |
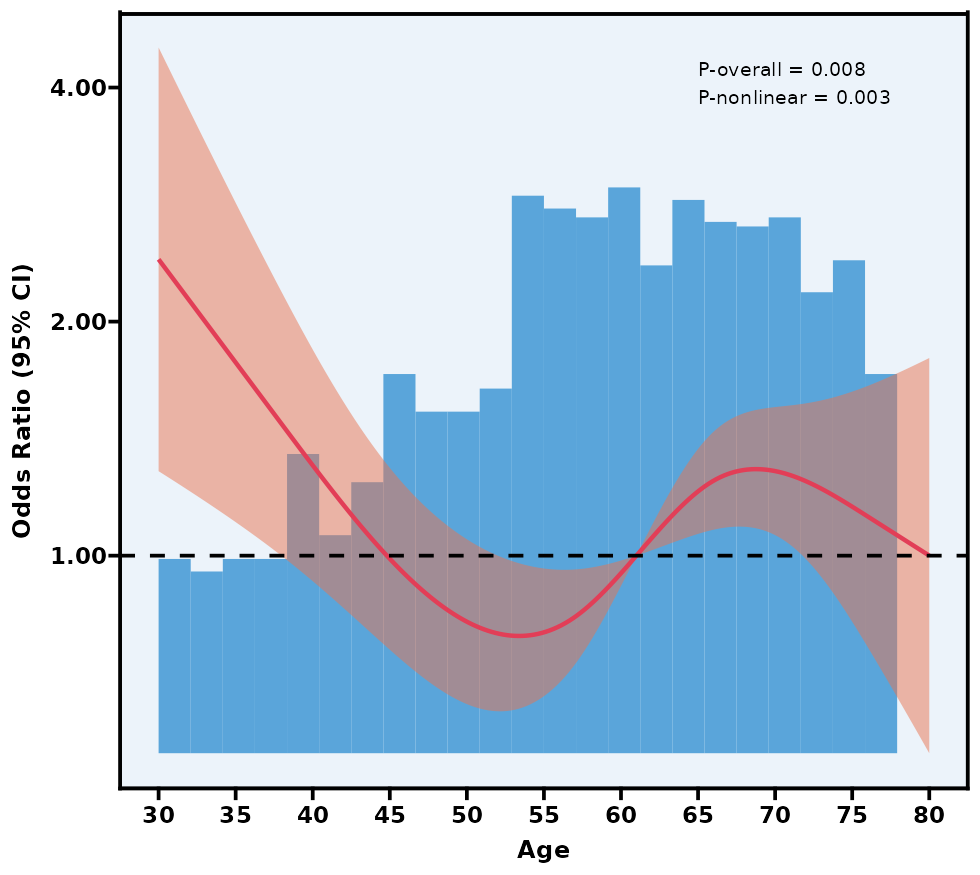 |
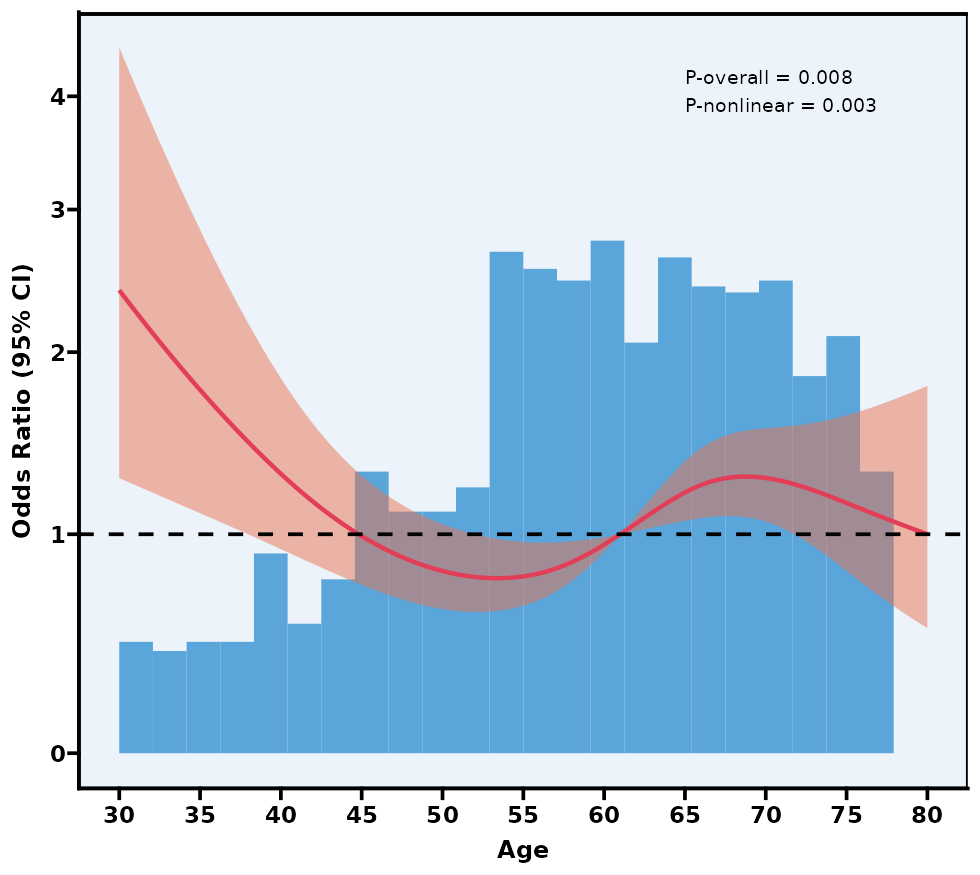 |
| RR值 | 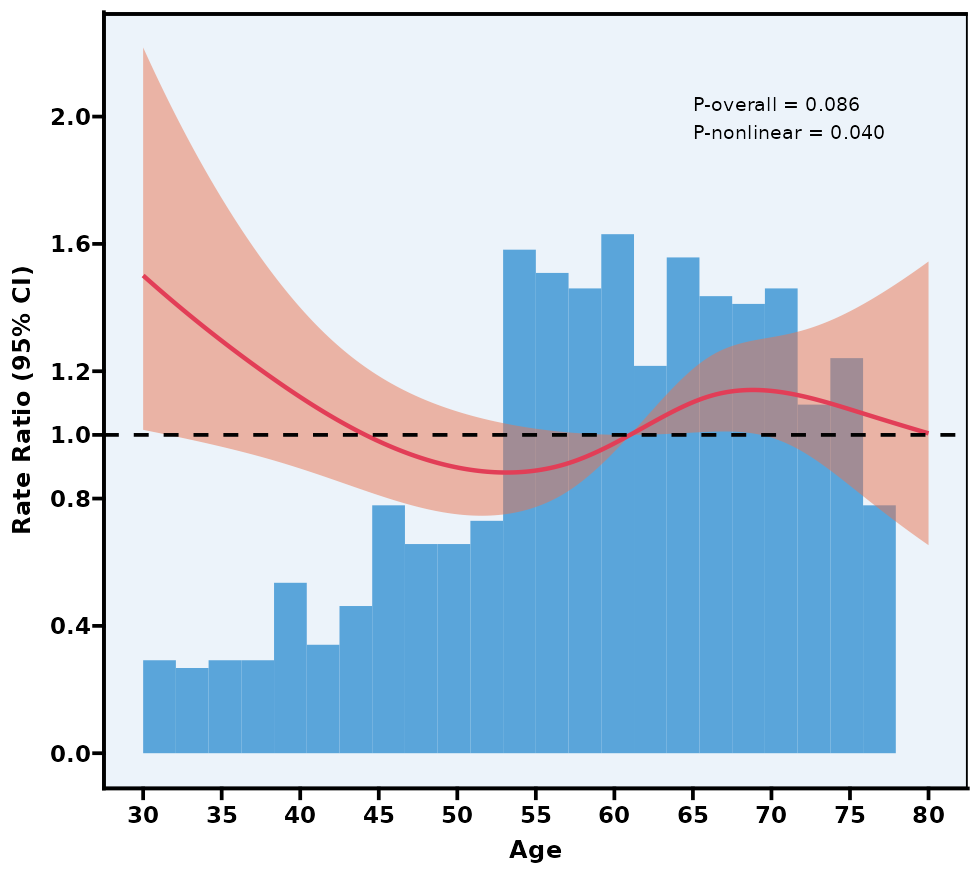 |
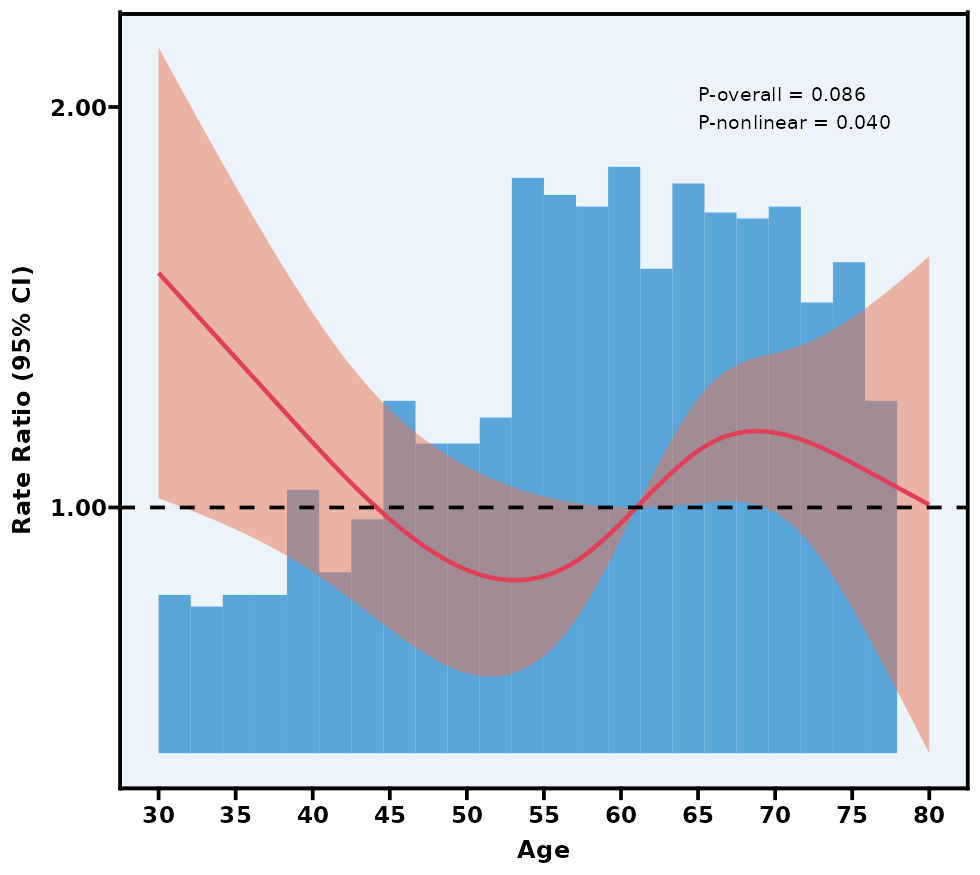 |
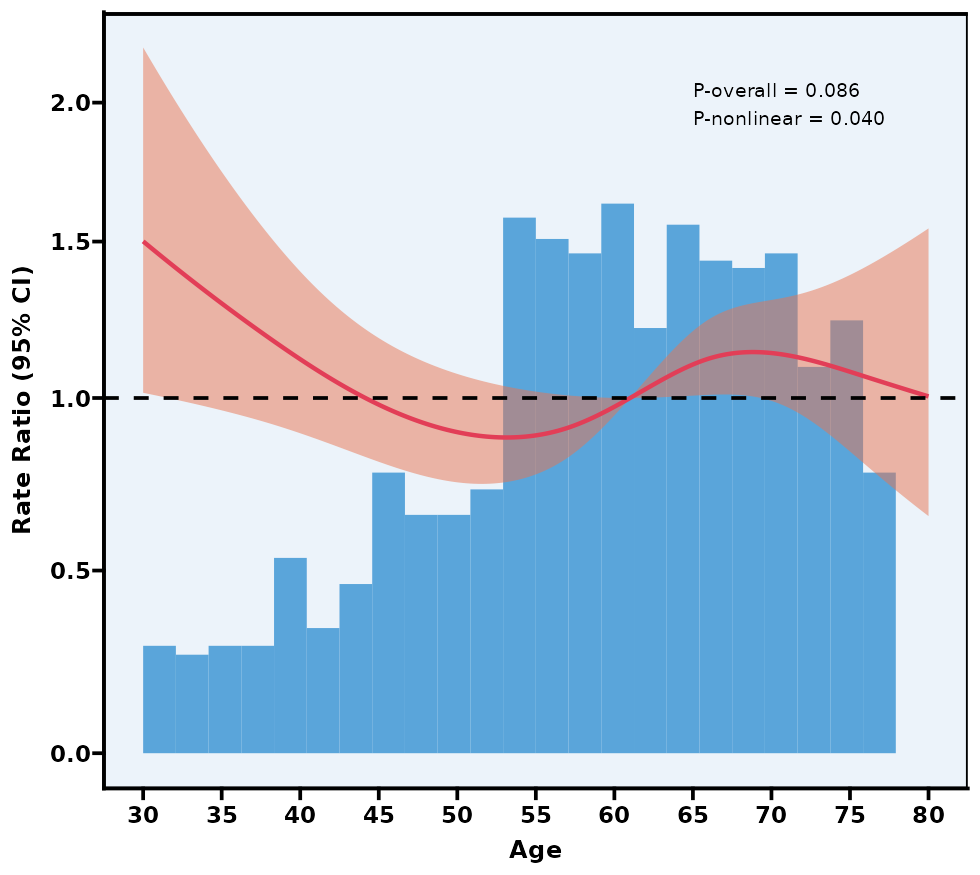 |
| HR值 | 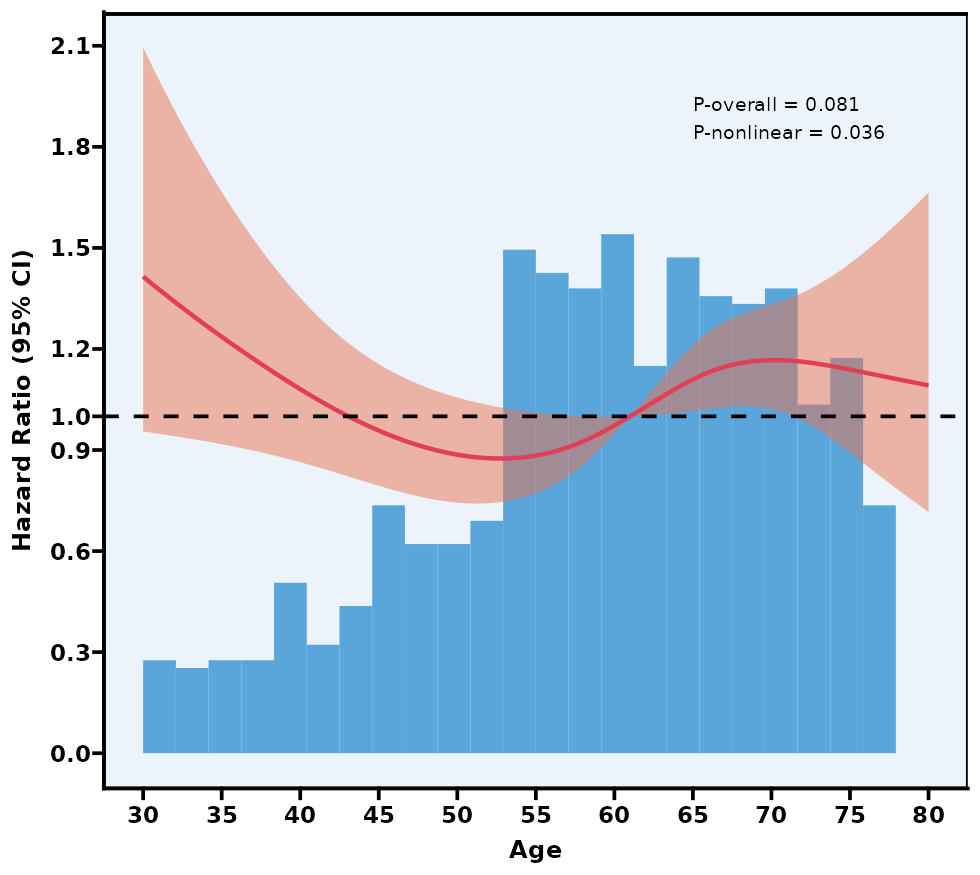 |
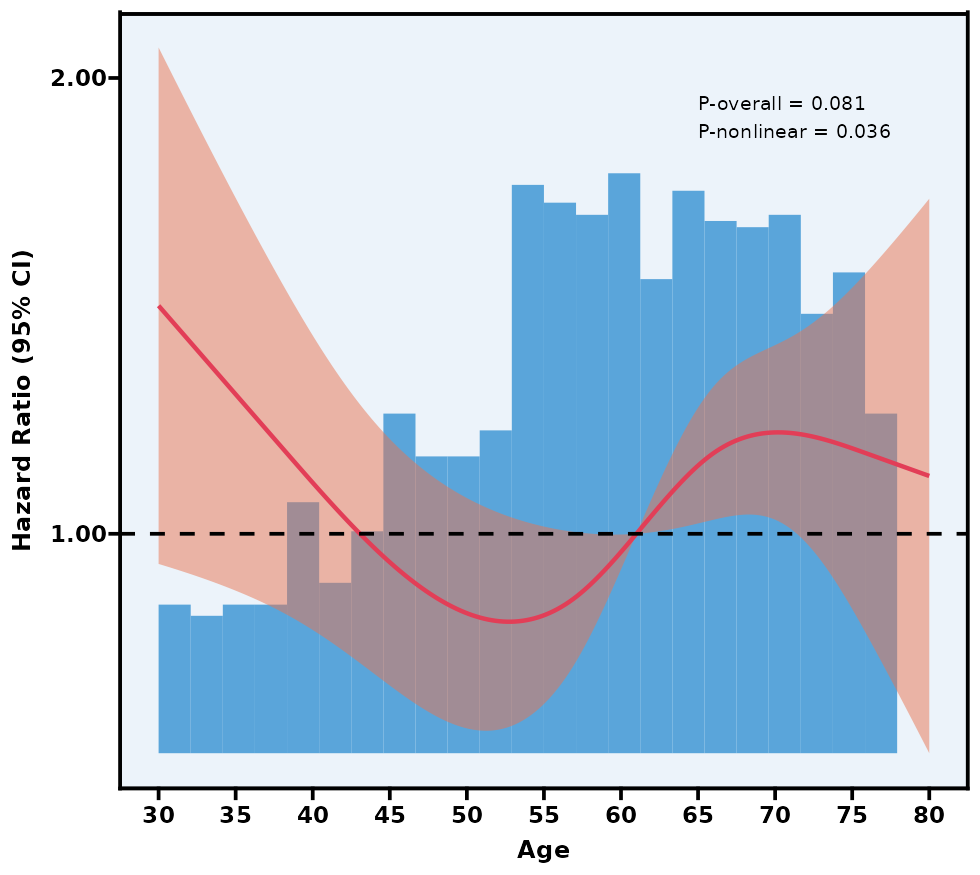 |
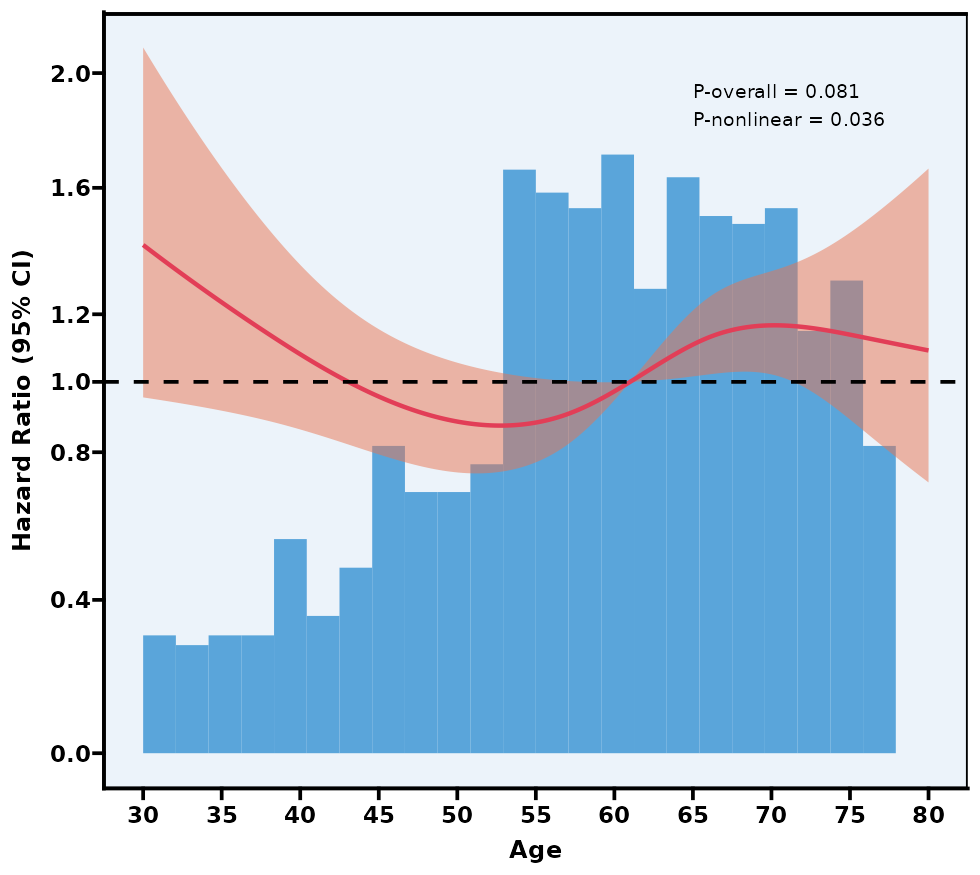 |
| Beta值 | 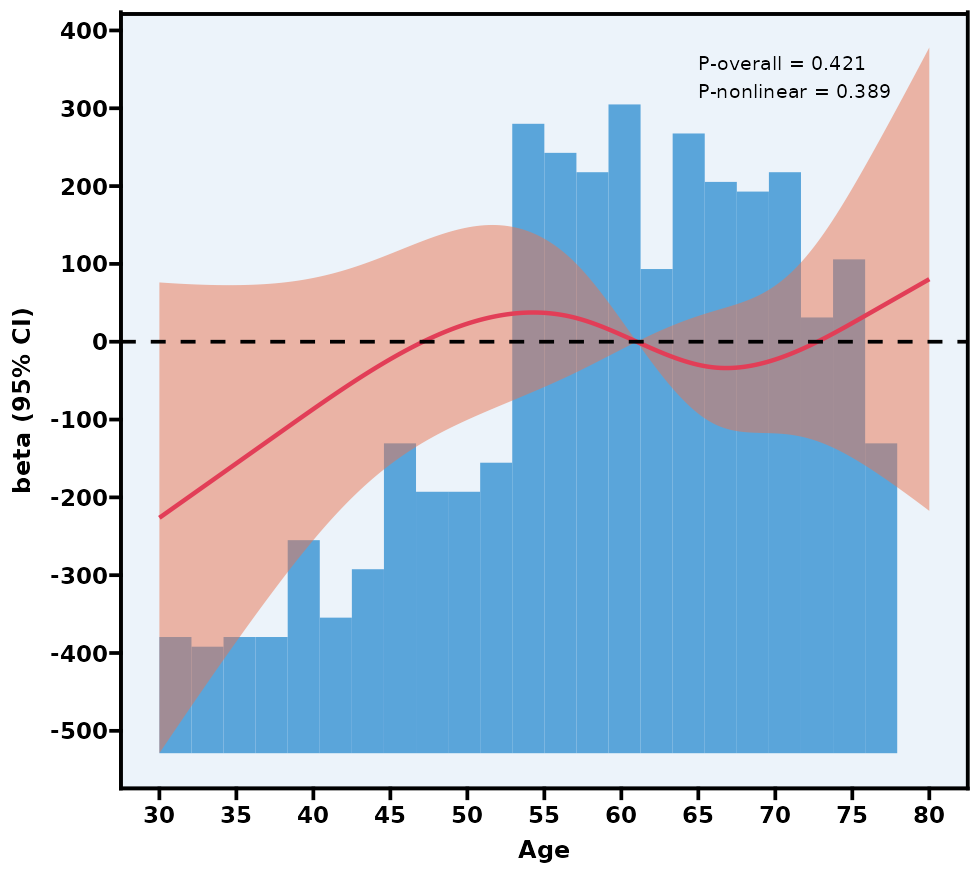 |
////////////////// ////////////////// ////////////////// ////////////////// |
////////////////// ////////////////// ////////////////// ////////////////// |
| Piecewise 线性回归 | Piecewise Cox 回归 | Piecewise Poisson 回归 |
|---|---|---|
 |
 |
 |

5.12.1 的基本原理
分段三次样条
RCS 的核心思想是将自变量区间划分为若干段,每段都用三次多项式进行拟合。各段多项式在交界处(节点处)不仅函数值相等,而且在一阶、二阶导数上也保持连续,这样就保证了整体曲线的光滑度。“限制性”处理
与一般的三次样条(Cubic Splines)相比,RCS 会在自变量区间的两端添加约束,避免在数据稀少的边缘区域出现过度振荡的情况。这种“限制性”可有效提高曲线在边缘的稳定性,也使结果更容易解释和呈现。节点数与位置
RCS 需要用户事先指定节点的数量(knots),以及如何放置这些节点。常见做法有:固定 knot 数量(如 3~7 个),将节点等分或放置在数据分布的分位数(quantiles)处;
通过模型比较(例如 AIC、BIC)或交叉验证自动寻找最优 knot 数与位置。
参考点(Reference Value)
RCS 在可视化时,通常需要选定一个参考点(如中位数或某一临床上关注的值)。模型估计出的曲线即代表:当自变量在其他值时,相对于这个参考点的效果量(如 OR、HR、RR 或回归系数)的变化情况。
5.12.2 在医学科研中的应用及优势
多因素回归中的非线性处理
许多医学指标(如血压、血糖、BMI、实验室指标等)与预后并非简单的直线关系,往往存在某些阈值或上下限效应。通过 RCS,可以更好地识别并展示这些潜在的非线性趋势。寻找“拐点”与阈值效应
医学上常关心某些关键数值,例如“当血压高于某点后,心血管事件风险突然上升”。RCS 曲线可在直观上提示是否存在拐点;若拐点明显,还可进一步做分段回归(Piecewise 回归)来量化不同区间的影响强度。对流行病学大数据的灵活拟合
在流行病学和公共卫生研究中,样本量大且变量复杂,RCS 可在不损失太多自由度的情况下提供更准确的拟合,同时也避免将连续变量武断地分组(如分成“高、中、低”),从而减少信息损耗。可视化优势
RCS 所绘制的曲线可以同时显示置信区间并与自变量的实际分布相结合,让读者更直观地理解某个风险因素的“安全区间”或“高风险区间”。
5.12.3 举例说明
例 1:BMI 与心血管疾病风险
研究背景:在大量的队列研究中,体重指数(BMI)与心血管事件风险并非简单的线性正相关。有些人观察到当 BMI 过低时,风险同样升高,出现 U 型关系。
方法:采用 RCS 在 Cox 回归模型中,将 BMI 作为连续变量引入,并设置 4 个节点(默认放置在 5%、35%、65%、95% 分位数)。结果发现,BMI≈22 kg/m² 左右时心血管风险最低,过高或过低都增加事件发生率。
意义:帮助临床或公共卫生人员确定 BMI 更精确的风险趋势范围。
例 2:肿瘤标志物水平与预后
研究背景:肿瘤患者常做血清或组织标志物检测(如 CA125、AFP 等),其与生存结局(如总体生存期 OS 或无进展生存期 PFS)之间的关系可能呈复杂曲线。
方法:将标志物值作为自变量进入 Cox 回归模型时,用 RCS 检测可能的拐点。
结果:发现标志物水平特别低时,风险稍高,中等范围内相对风险最低,而超过某一阈值后风险又明显攀升,呈 U 型或 J 型曲线。
意义:为个体化治疗或随访策略提供参考:如果在“中等安全区间”则随访频率可适当减少;而当标志物升至阈值以上,就应及时干预或加强随访。
总结:RCS 对于有理由怀疑“自变量-结局”存在非线性关系的医学研究而言,是一项既灵活又实用的方法。它能帮助我们更准确地呈现真实世界的复杂关联,避免线性假设带来的偏误。在临床和流行病学的高分论文中,RCS 越来越成为一种常见且被审稿人认可的分析手段。
5.12.4 功能特点
本模块让您能够快速、高效地生成符合高分SCI期刊要求的RCS图像和相应的论文描述:
多回归类型一站式支持
适用于 线性回归(连续结局)、Logistic 回归(二分类结局)、Log-Binomial 回归(二分类结局)、Ordinal Logistic 回归(有序多分类结局)、Cox 回归(生存数据)、以及 Poisson/Quasipoisson 回归(计数数据)等多种模型场景。
只需在侧边栏菜单选择对应的结局类型,即可自动匹配相应回归方法。
智能节点(knot)选择及灵活配置
可使用“根据最小 AIC 自动计算”让软件自动在 3~7 个节点之间迭代选择最优解;或直接手动设置节点数(knot)以满足特定研究需求。
节点位置和数量在结果中会清晰呈现,便于论文中汇报和解释。
支持多种风格的限制性立方样条(RCS)图
风格一:基础 R 绘图(Base Graphics)简洁直观;
风格二:华丽版(ggplot2 + 自定义配色),可调节对数刻度、直方图高度、整体背景,适合杂志对美观的要求;
风格三:朴素版(ggplot2),尤其适合黑白刊物或需简洁风格的场合。
全程只需在右侧的“图像外观设置”中滑动或下拉选择,即可实时预览并下载高清图。
自动与手动相结合的拐点探索
可根据眼见的曲线形状(U 型、∩ 型或其他)自动定位最高点/最低点为拐点,也可手动拖拽滑块精确设置任意折点值。
对于明显的阈值或转折位置,可直接在图像中标记并输出,用于后续分段回归或论文讨论。
一键分段(Piecewise)回归
结合拐点结果,可自动对自变量进行分段,使用传统 GLM 或 segmented 包进行分段回归。
分段后可得到各区间的斜率、OR/HR/RR 等信息,以及置信区间,帮助揭示不同数值区间下的差异。
自动生成符合论文格式的图文报告
系统可一键导出 Word 文档,包含 “Objective, Methods, Results” 等方法学描述,以及高质量 RCS 曲线插图。
无需反复手工排版,大大节省在撰写 SCI 论文或课题报告时的时间与精力。
R 源代码及数据一键查看或下载
提供完整的 R 代码自动生成功能,包含 RCS 或分段回归分析的全部脚本,便于审稿人或课题组成员在本地 R 环境中复现结果。
数据集 (
dt.RData) 同样可一并下载,实现无缝对接与二次开发。
通过以上功能,用户能在可视化、拐点探索、分段分析、以及论文写作方面实现全面助力,轻松生成符合高分期刊要求的精美 RCS 图和配套报告。
5.12.5 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.12.7 绘制 RCS 曲线
点击上方第二个 Tab “生成限制性立方样条图” 进入主功能界面。此界面又分为 左右两大区域:
左侧侧边栏(Sidebar):主要用于设置模型参数(如结局变量、协变量、结局类型、Knot 节点数等),以及最基础的图形外观(如对数刻度、参考值设置等)。
右侧主区域(Main Panel):展示 RCS 模型输出、以及三种风格的 RCS 图像。
下面详细介绍侧边栏的各项配置:
模型设置
回归类型:根据结局变量的类型,选择 “二分类变量(Logistic 回归)”、“二分类变量(Log-Binomial 回归)”、“生存变量(Cox 回归)”、“有序多分类(Ordered Logistic)”、“连续型变量(Linear 回归)”或“计数资料(Poisson/Quasipoisson)” 等。
选择结局变量:如果选择 Logistic 回归,需要指定二分类结局(如“是否好转”),同时在下拉菜单中选中哪个水平代表“事件=1”;若是 Cox 回归,需要依次指定 time、status;若是线性回归则直接选一个数值型变量等。
选择自变量(X):只能选择一个数值型变量用于做 RCS 曲线。如果你在菜单里找不到想要的变量,说明它在“数据准备”模块中尚未被设置成 numeric。
选择协变量(Covariates):可多选或不选,用于做多因素回归时的调整。建议不要一次性选过多协变量,以免共线性。
设置节点数(Knot)
- 可选择“根据最小 AIC 自动计算”(系统会在 3-7 个节点内自动迭代并选出 AIC 最小的方案),或者“手动设置”为 3-7。
设置参考点(Reference Value)
- 参照点用于计算纵坐标上每个 X 值相对这个参考值的 OR、HR、Beta 等。默认取中位数或 50% 分位数,可根据需要改为 10% 分位数等。参考点的不同只会影响曲线在纵轴上的“基准高低”,不影响曲线形状。
点击“生成/更新限制性立方样条图”:完成上述设置后,点击此按钮开始建模,随后右侧会出现分析结果。
右侧输出
- RCS 建模结果(rms 包输出):显示 knot 节点位置、AIC、P 值等模型概要信息,以及一些回归系数、模型拟合优度等。注意,这里只是基础表格,主要用于审查模型是否正常。
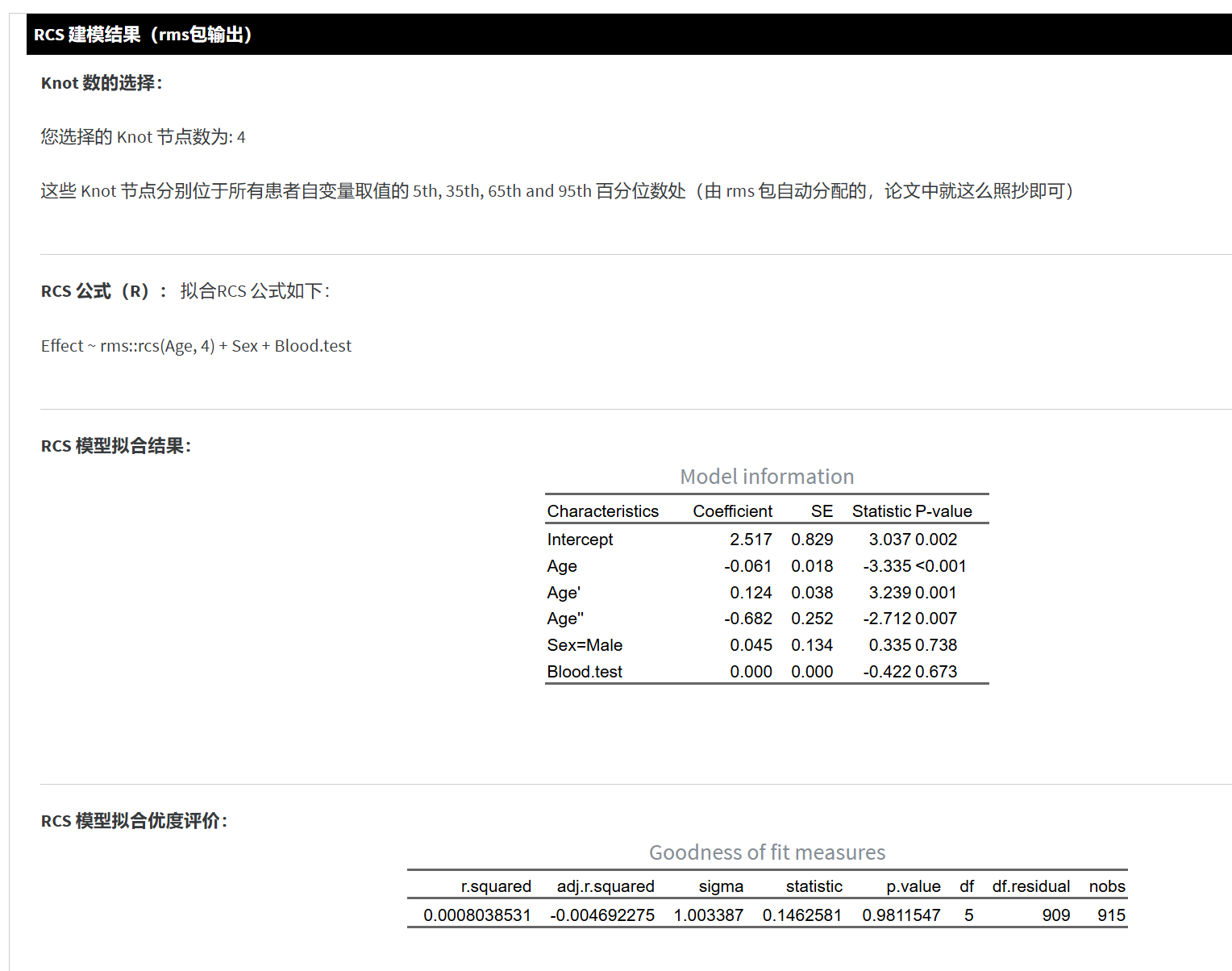
三种风格的 RCS 图像:
风格一:Base R Graphics(基础 R 包绘制)
相对朴素的基础绘图风格。
右侧可调节图片大小、颜色(黑白、玫瑰红、蓝色等),并决定是否在纵轴使用对数刻度等。
风格二:华丽版 RCS 曲线(ggplot2 包 + 自定义配色)
参考顶刊文献配色,带有半透明置信区间条带和直方图(表示数据分布密度)。
右侧可调节对数/伪对数坐标、直方图高度及条数、配色主题等。
可将置信区间与直方图都呈现在一幅图里,适合对外展示、发表。
风格三:朴素版 RCS 曲线(ggplot2 包,适合黑白杂志)
样式更简洁,黑白或单色系列。
同样可在右侧调节直方图外观、对数刻度等。
注意:如果本模块检验出的“P for nonlinear”较大(>0.05),可说明自变量与结局之间的关系可能更趋近于线性,此时完全可以用传统的“线性”假设进行普通回归。若 P for nonlinear < 0.05,才有必要继续深入研究它的非线性特征。
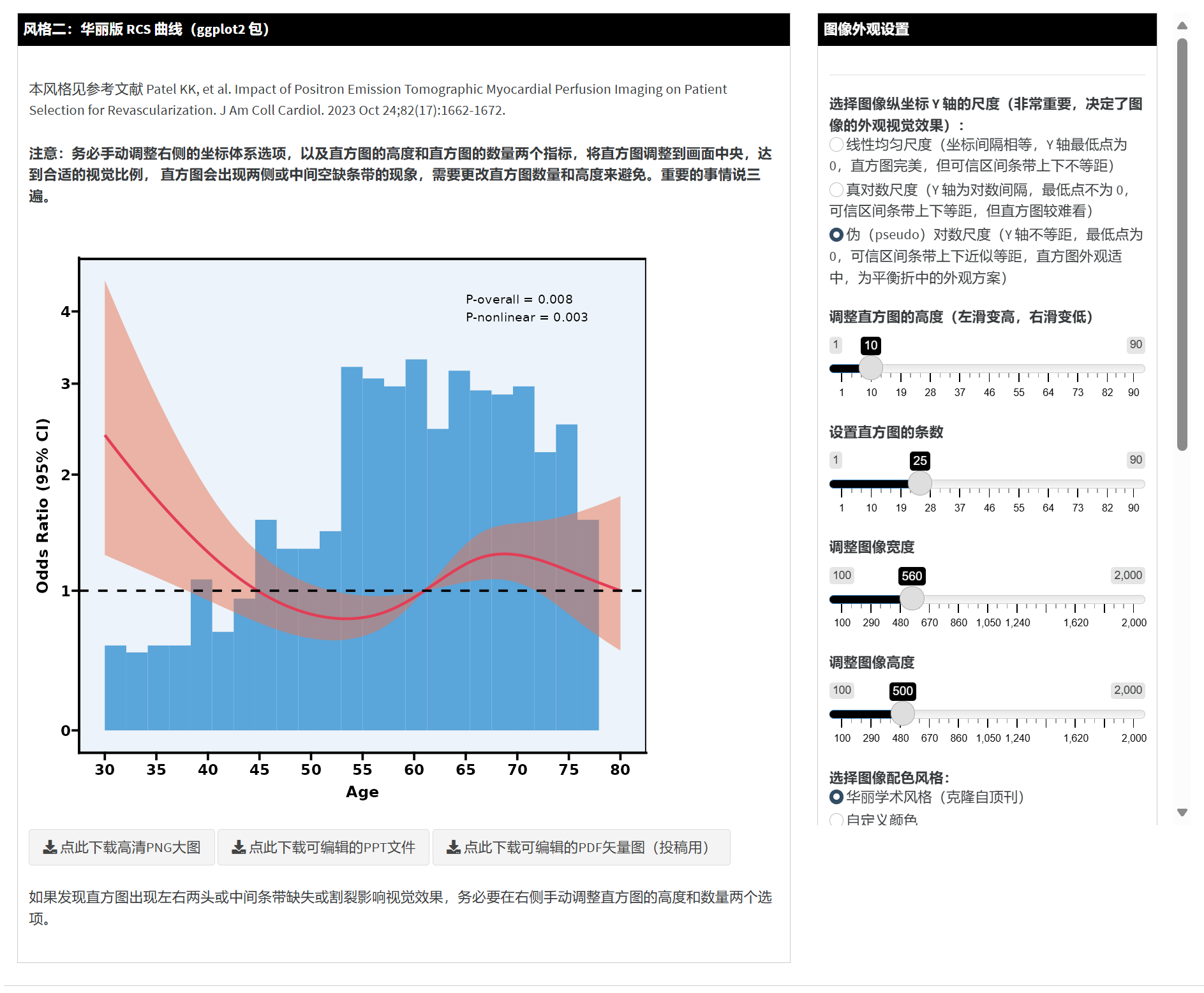
5.12.8 观察图像肉眼寻找折点的粗略位置(第 3 个 Tab)
在第 2 步生成的 RCS 图像中,如果曲线确实存在非线性,可以切换到本 Tab 做进一步观察。
选择拐点个数和类型:
不设置折点:如果曲线近似直线或没有明显拐点,可以停止于 RCS 阶段,不必分段。
在最低点设置折点:适用于 U 型曲线,且最低点确实在中部;若曲线两端才是最低点,不建议这样做。
在最高点设置折点:适用于 ∩ 型曲线。
手动输入折点:如果曲线呈 J 型、L 型或多段复杂变化,或者有临床/文献先验信息,可以拖拽滑块自行指定折点值。软件会在图上标记该点。
查看折点叠加后的 RCS 图:
会同时显示“华丽版”和“朴素版”两种风格,曲线上会出现一条垂直的虚线标记你选定或自动计算的拐点位置。
若要微调折点,可反复拖动滑块,直到感觉曲线上拐点位置与实际生物学意义较为匹配。
在临床研究中,折点往往用于提示“剂量或数值到了某个位置后,效果会发生转折”;如果能在文献中找到类似报道,也可直接采用既往经验折点。
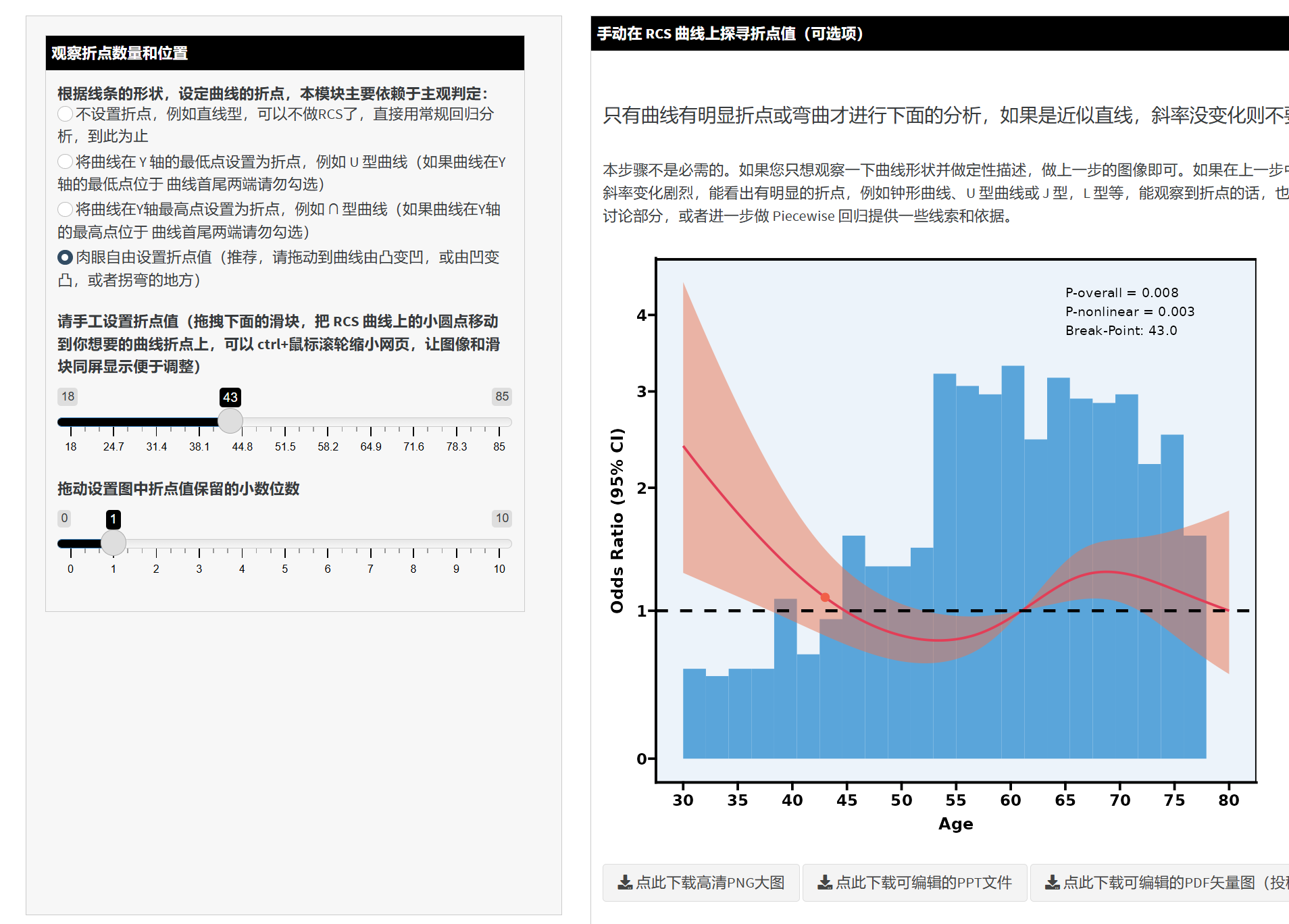
5.12.9 阈值效应和 piecewise 回归(第 4 个 Tab)
如果确有非线性,且对折点附近的转折效应感兴趣,我们通常会做 分段回归(Piecewise regression),以量化在不同区间的回归系数(OR/HR/RR/beta)。
点击进入“阈值效应和 piecewise 回归”:侧边栏将出现以下几个关键选项:
方法选择:
segmented包自动寻找折点- 设置一个或多个折点数量(npsi),系统会在给定数量下用迭代算法自动找最优位置;或者指定一个“起始值 psi”,让软件从该位置附近开始自动迭代定位折点。
人为指定折点
- 直接输入要分段的所有折点值,软件就会对每个区间做线性回归。
选择协变量:可与 RCS 分析时相同,也可自行更改。
生成 Piecewise 回归结果:点击“生成/更新 piecewise 回归分析结果”后,右侧会显示分段后的各区间斜率及其 95% CI、P 值等。
结果解读:
系统输出一份表格:展示每个分段区间内,该连续自变量对结局的回归系数(或 OR、HR、RR)及统计显著性。
还会给出一幅分段回归的可视化图:如果采用
segmented包自动寻点,曲线上会以折线或分段斜率的方式显示;若是“手动指定折点”,则会显示分段后的拟合线。
提示:Piecewise 回归并不是简单地把数据按某个阈值拆分成两组后各自做单独回归,而是直接在同一个模型中通过截断函数(Truncated function)实现分段的线性拼接,因此在区间交界处保持连续,并能很好体现一条连续变量可能在不同区间中存在不同的风险趋势。

5.12.10 下载 word 报告(第 5 个 Tab)
在这里可一键导出 Word 文档,以便写论文或留档。下载之前需先完成前面 RCS 或 piecewise 回归的分析。文档包含以下内容:
Objective & Methods:关于本次 RCS 或 piecewise 分析的文字描述
Results:自动带入 RCS 模型结果、P 值、节点位置等
图像:自动插入一张 RCS 曲线或分段回归示意图
请注意:
下载后若用微软 Office 打开,排版能更好地保留;WPS 有时会有兼容问题。
如果希望对报告中的文字进行修改或补充,可直接在 Word 中手动编辑。
5.12.11 查看 R 源代码和原始输出(第 6 个 Tab)
下载 dt.RData:先点击“下载源代码配套的数据集 dt”,之后在 RStudio 等环境中执行
load("dt.RData")即可加载同样的数据集。查看或下载 R 源代码:下方会显示两块黑底区域:
RCS 建模代码及输出:可复制到本地 R 运行。
Piecewise/segmented 代码及输出:同理。
二次验证:审稿人或课题组内成员如想复现结果,可直接在本地运行下载的 R 代码和数据。
5.12.12 方法学要点与软件依赖包
方法学要点
RCS 的原理:通过在自变量上设置若干节点(knots),将三次多项式片段连接成一条连续、光滑的曲线;在两端做限制,避免过度振荡。
P overall 和 P nonlinear:
P overall 主要检验“这条 RCS 曲线整体上是否与结局有显著关联”;
P nonlinear 检验曲线是否具有显著非线性(若 >0.05,则可视为线性)。
Piecewise 回归:当 P nonlinear 显著或在生物学上明确存在阈值、转折点时,可进一步做分段回归,用传统 GLM 或
segmented包自动寻点来量化每段斜率差异。
软件和 R 包版本
后台使用:
R 4.2.2RCS 回归分析包:
rms图形绘制:
ggplot2,辅助美化用ggprism,基础绘制方式则基于Base R GraphicsP 值等统计:
rms包分段回归:
base中的glm()做传统分段,或segmented包自动寻找折点
5.12.13 常见问题
生成的 RCS 曲线纵坐标值的含义?
- 纵坐标是该自变量在各取值下相对于“参考点(Reference Value)”的 OR、HR、或 Beta 等。它仅表示“相对”量,不宜直接解读为绝对的危险度。
若非线性不显著该怎么办?
- 可以直接改用普通线性假设做回归。RCS 通常用于捕捉非线性;若线性更优,则使用线性模型即可。
如何处理协变量缺失?
- 建议在“数据准备”模块对缺失做适当填补(插补)或删除,以免在 RCS 或分段回归阶段产生意外报错。
曲线两端置信区间很宽怎么办?
- 这是常见现象。两端往往样本少,估计不稳定。如果不关心边缘区域,可在描述结果时稍作简化。
图中直方图显示不理想,出现空缺或严重重叠?
- 可在图像外观设置区域调整 “直方图的高度”和 “直方图的条数”,让区间分得更细或更粗,从而保证分布与曲线在视觉上对齐。
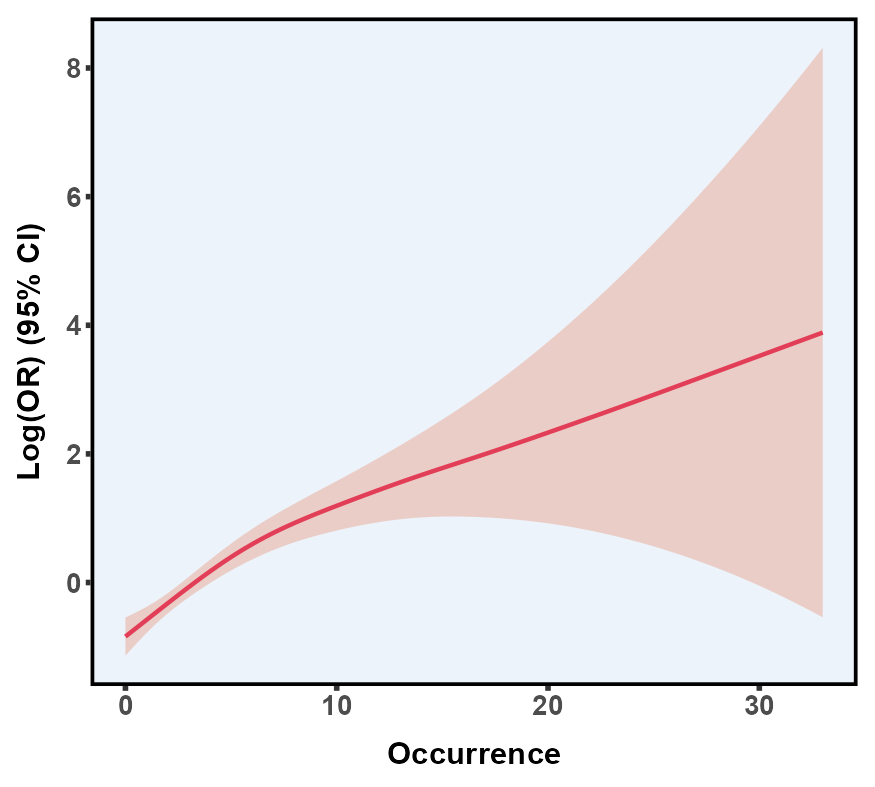
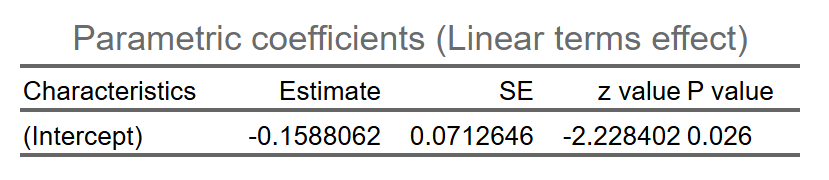
5.13 广义相加模型 GAM
广义相加模型(Generalized Additive Models, GAM) 是一种灵活的统计建模方法,可以处理自变量和因变量之间的非线性关系。GAM 将回归问题扩展到更广泛的模型形式,不仅支持传统的线性回归,还能够使用平滑函数描述自变量与因变量之间的非线性关系。因此又被称为万能回归模型。
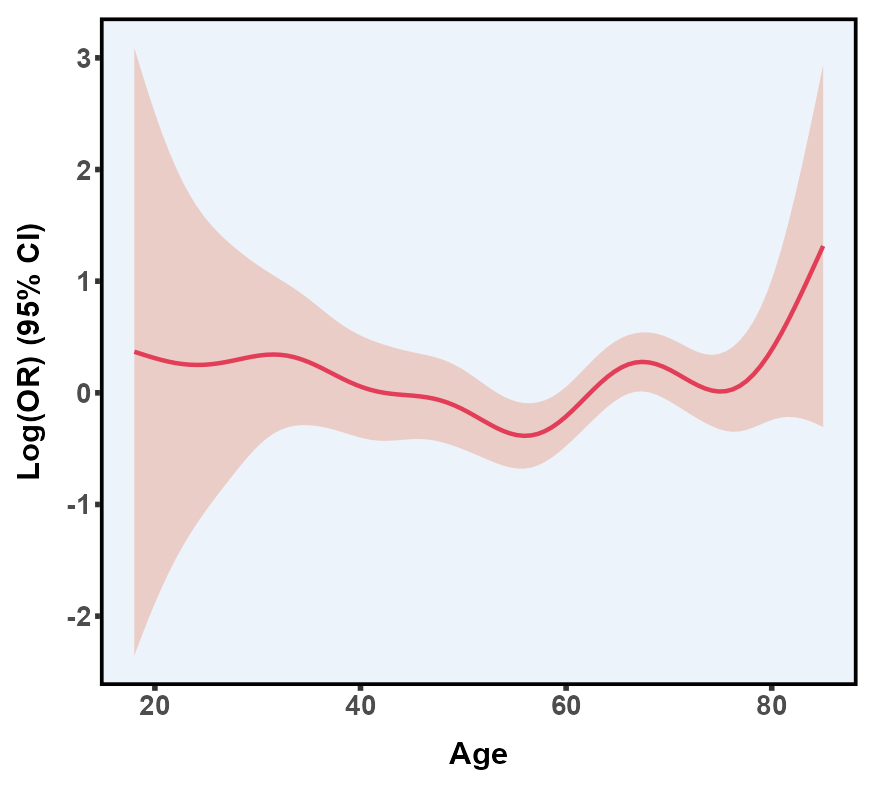 |
 |


| Piecewise 线性回归 | Piecewise Cox 回归 | Piecewise Poisson 回归 |
|---|---|---|
 |
 |
 |

5.13.1 GAM 的基本原理
平滑函数
GAM 的核心思想是利用平滑函数(如样条函数)来拟合自变量与因变量之间的关系。与传统回归模型不同,GAM 可以灵活地捕捉自变量和因变量之间复杂的非线性关系。回归与平滑的结合
在 GAM 中,自变量与因变量的关系被分为线性部分和非线性部分。线性部分通常是固定效应,而非线性部分则通过平滑函数来建模。灵活性和可解释性
GAM 具有较高的灵活性,可以适应数据的非线性模式,同时保持模型的可解释性。通过选择合适的平滑函数和回归模型,GAM 适用于多种类型的数据分析任务。选择合适的平滑函数
在 GAM 中,可以选择不同的平滑函数。平滑函数的选择依赖于自变量的分布和数据的特性。
5.13.2 GAM 在医学科研中的应用及优势
处理非线性关系
许多医学研究中的数据呈现出非线性关系,例如血糖水平与疾病风险之间的关系。在这种情况下,GAM 能够通过平滑函数有效地捕捉这些非线性趋势。多因素回归中的非线性建模
在多因素回归中,GAM 可以对自变量与因变量的关系进行灵活建模,特别是在存在多个因素时,能够更好地识别潜在的非线性关系。个体化医疗分析
GAM 可以帮助临床研究人员在个体层面上识别关键的健康指标,从而为个体化医疗方案提供支持。灵活的模型设定
GAM 允许用户根据数据的特性灵活选择平滑函数,避免了强假设的局限性。
5.13.3 举例说明
例 1:BMI 与心血管疾病风险
研究背景:在大量的队列研究中,体重指数(BMI)与心血管事件风险并非简单的线性正相关。有些人观察到当 BMI 过低时,风险同样升高,出现 U 型关系。
方法:采用 GAM 在 Cox 回归模型中,将 BMI 作为连续变量引入,并设置合适的平滑函数进行分析。
结果:发现,BMI ≈ 22 kg/m² 时心血管风险最低,过高或过低都增加事件发生率。
意义:帮助临床人员确定 BMI 更精确的风险趋势范围。
例 2:血压与心脏疾病的关系
研究背景:血压水平与心脏疾病的关系被认为是非线性的,特别是高血压对心脏事件的风险影响较大。
方法:采用 GAM 模型,在 Cox 回归分析中引入血压作为平滑自变量,并控制其他协变量。
结果:结果表明,当血压升高至某个阈值时,风险显著增加,展示了血压与心脏疾病的非线性关系。
总结:GAM 对于有理由怀疑“自变量-结局”存在非线性关系的医学研究而言,是一项灵活且实用的方法。它能够帮助研究人员揭示和解释真实世界中复杂的非线性关系,并且在临床和流行病学的高分论文中得到了广泛应用。
5.13.4 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
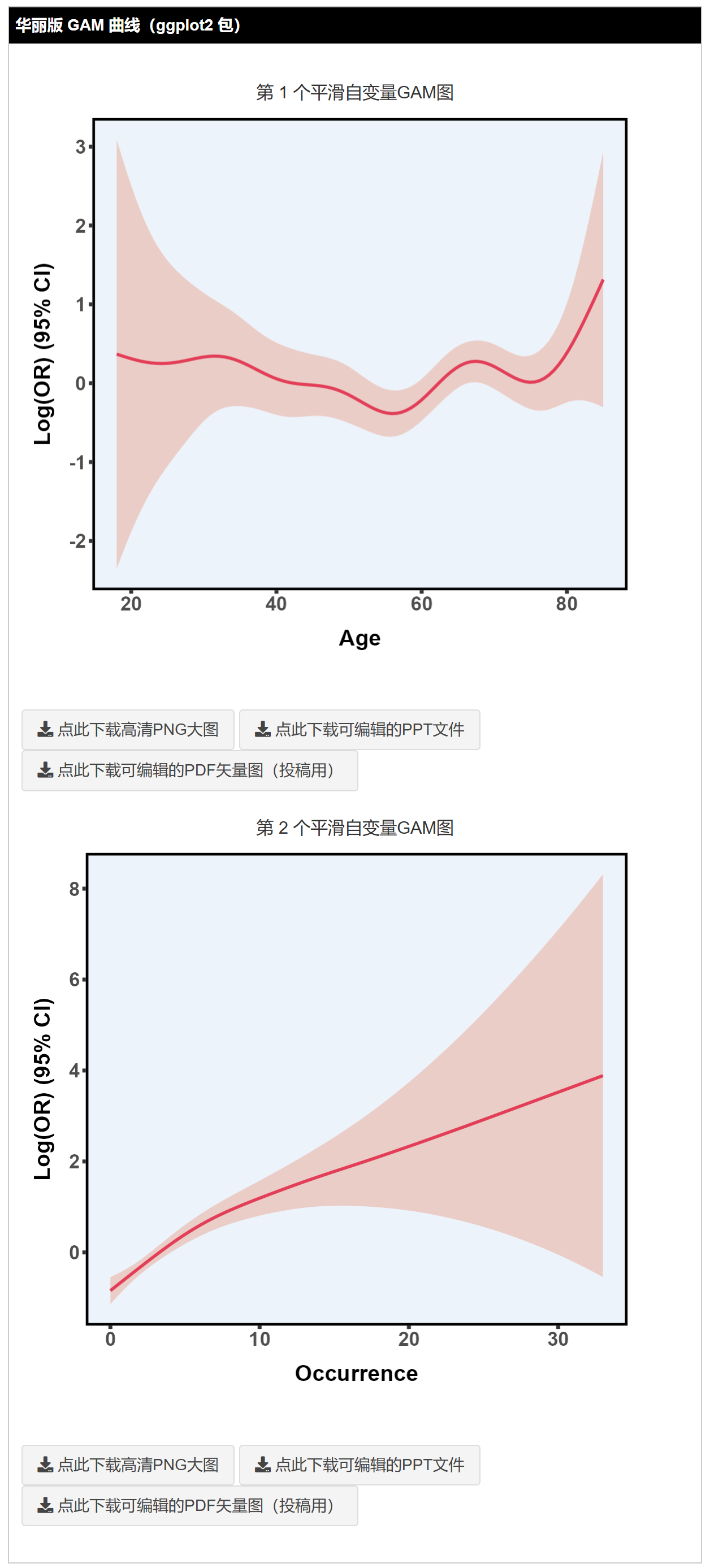
5.13.6 生成 GAM 曲线
点击上方第二个 Tab “生成广义相加模型曲线” 进入主功能界面。此界面分为 左右两大区域:
左侧侧边栏(Sidebar):主要用于设置模型参数(如结局变量、协变量、结局类型等),以及图形的基本外观设置。
右侧主区域(Main Panel):展示 GAM 模型输出,并展示三种风格的 GAM 图像。
5.13.7 阈值效应和 piecewise 回归(第 4 个 Tab)
如果确有非线性,且对折点附近的转折效应感兴趣,我们通常会做 分段回归(Piecewise regression),以量化在不同区间的回归系数(OR/HR/RR/beta)。
点击进入“阈值效应和 piecewise 回归”:侧边栏将出现以下几个关键选项:
方法选择:
segmented包自动寻找折点- 设置一个或多个折点数量(npsi),系统会在给定数量下用迭代算法自动找最优位置;或者指定一个“起始值 psi”,让软件从该位置附近开始自动迭代定位折点。
人为指定折点
- 直接输入要分段的所有折点值,软件就会对每个区间做线性回归。
选择协变量:可与 GAM 分析时相同,也可自行更改。
生成 Piecewise 回归结果:点击“生成/更新 piecewise 回归分析结果”后,右侧会显示分段后的各区间斜率及其 95% CI、P 值等。
结果解读:
系统输出一份表格:展示每个分段区间内,该连续自变量对结局的回归系数(或 OR、HR、RR)及统计显著性。
还会给出一幅分段回归的可视化图:如果采用
segmented包自动寻点,曲线上会以折线或分段斜率的方式显示;若是“手动指定折点”,则会显示分段后的拟合线。
提示:Piecewise 回归并不是简单地把数据按某个阈值拆分成两组后各自做单独回归,而是直接在同一个模型中通过截断函数(Truncated function)实现分段的线性拼接,因此在区间交界处保持连续,并能很好体现一条连续变量可能在不同区间中存在不同的风险趋势。

5.13.8 下载 word 报告(第 5 个 Tab)
在这里可一键导出 Word 文档,以便写论文或留档。下载之前需先完成前面 GAM 或 piecewise 回归的分析。文档包含以下内容:
Objective & Methods:关于本次 GAM 或 piecewise 分析的文字描述
Results:自动带入 GAM 模型结果、P 值、节点位置等
图像:自动插入一张 GAM 曲线或分段回归示意图
请注意:
下载后若用微软 Office 打开,排版能更好地保留;WPS 有时会有兼容问题。
如果希望对报告中的文字进行修改或补充,可直接在 Word 中手动编辑。
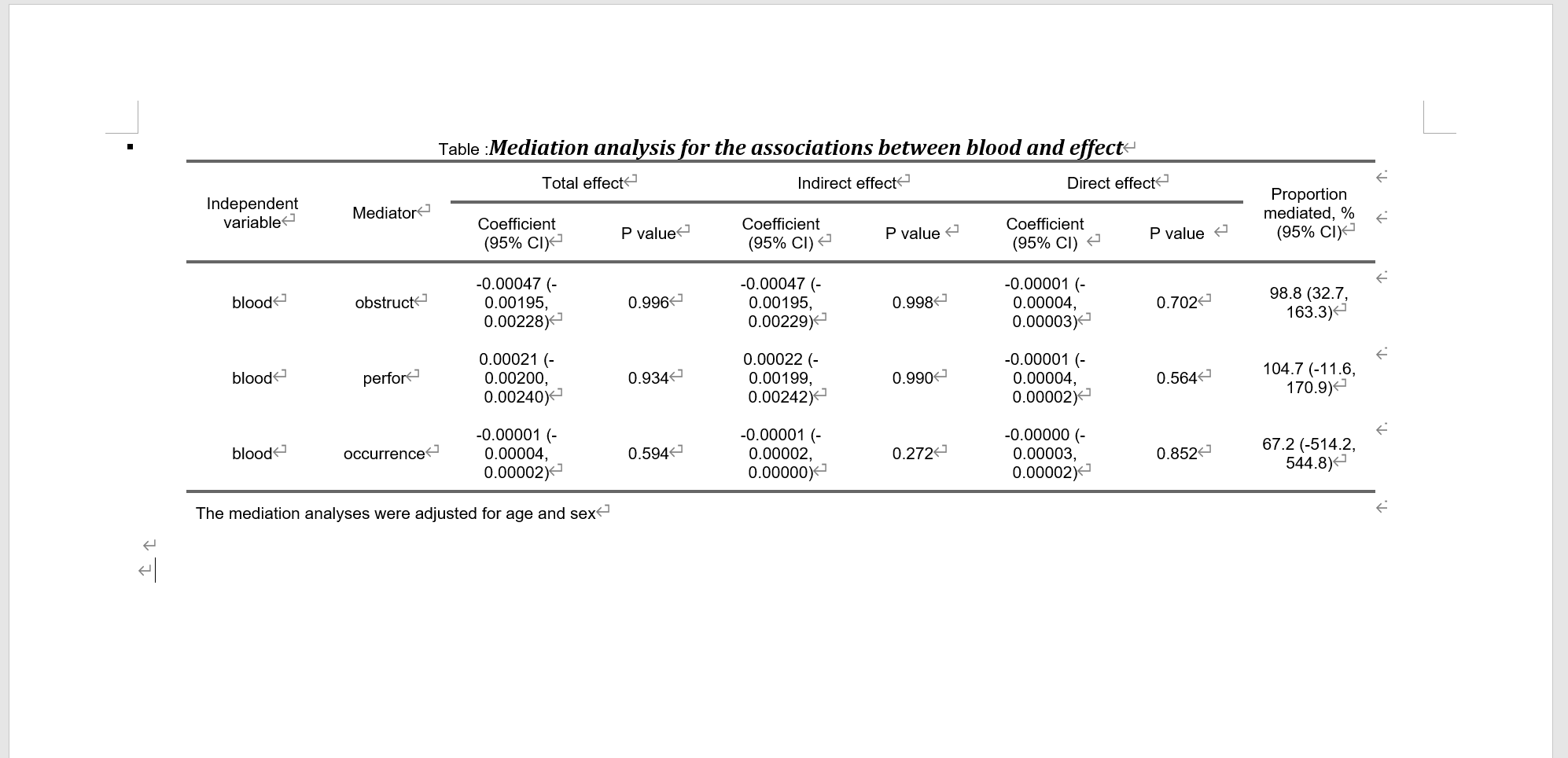
5.14 因果中介效应(mediation包,支持连续性/二分类/有序分类/生存资料)
因果中介分析 (Causal Mediation Analysis)
定义: 因果中介分析是一种统计方法,用于探索一个变量如何影响另一个变量的过程或机制。具体来说,它考察一个或多个中介变量是否在因变量和自变量之间起到中介作用,以及这种中介作用的大小。
原理: 在因果中介分析中,我们主要关心三个变量:自变量(X)、因变量(Y)和中介变量(M)。基本的思想是,自变量首先影响中介变量,然后中介变量再影响因变量。通过这种方法,我们可以分解自变量对因变量的总效应为两部分:直接效应和通过中介变量的间接效应。
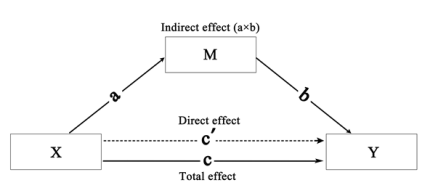
使用场景:
在心理学研究中,探索某种心理干预如何影响结果,并通过哪些心理机制产生这种影响。
在经济学中,研究某种政策如何影响经济增长,并通过哪些渠道实现。
在医学研究中,探索某种药物或治疗如何影响健康结果,并通过哪些生物机制起作用。
医学研究的例子: 假设我们想要研究某种药物是否可以通过降低血压来减少心脏病的风险。在这里,药物治疗是自变量(X),心脏病的风险是因变量(Y),而血压是中介变量(M)。通过因果中介分析,我们可以分析药物治疗对心脏病风险的直接效应和通过降低血压的间接效应。如果我们发现间接效应显著,这意味着药物确实可以通过降低血压来减少心脏病的风险。
总之,因果中介分析为我们提供了一种强大的工具,可以更深入地理解变量之间的关系和作用机制。
mediation包是R语言中的一个专门用于进行因果中介分析的包。它提供了一系列的函数和工具,使研究者能够轻松地进行中介效应的估计、检验和解释。本模块基于mediation包进行中介分析,并用Bootstrap的方法来估计中介效应的置信区间,这种方法对于非正态分布的数据特别有用。
mdiation包的框架(引自作者论文):
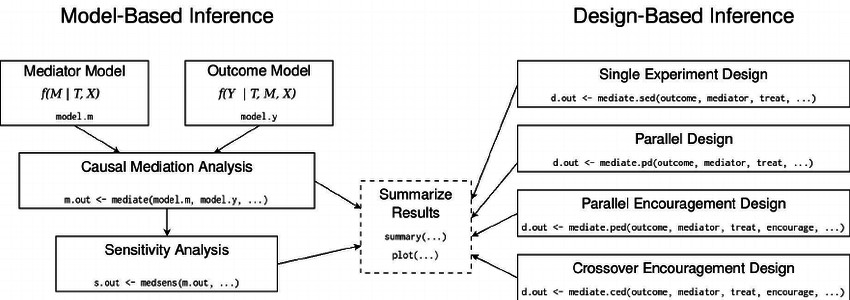
但是,mediation包原始输出的结果很粗糙,例如:
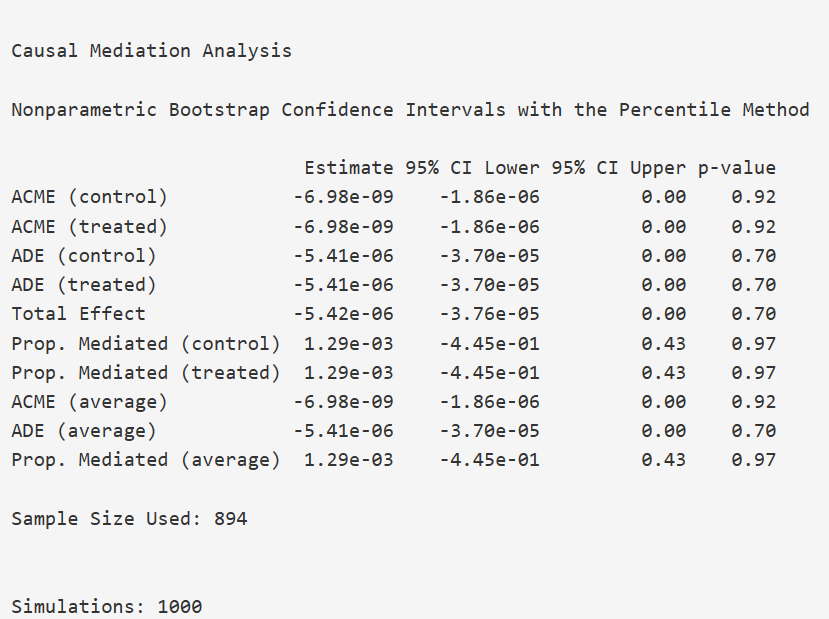
面对这个晦涩的结果,大多数人也蒙圈了,也不知道啥意思,折腾两天就放弃了。
而学术期刊上用medation包分析后投稿的表是这样的:
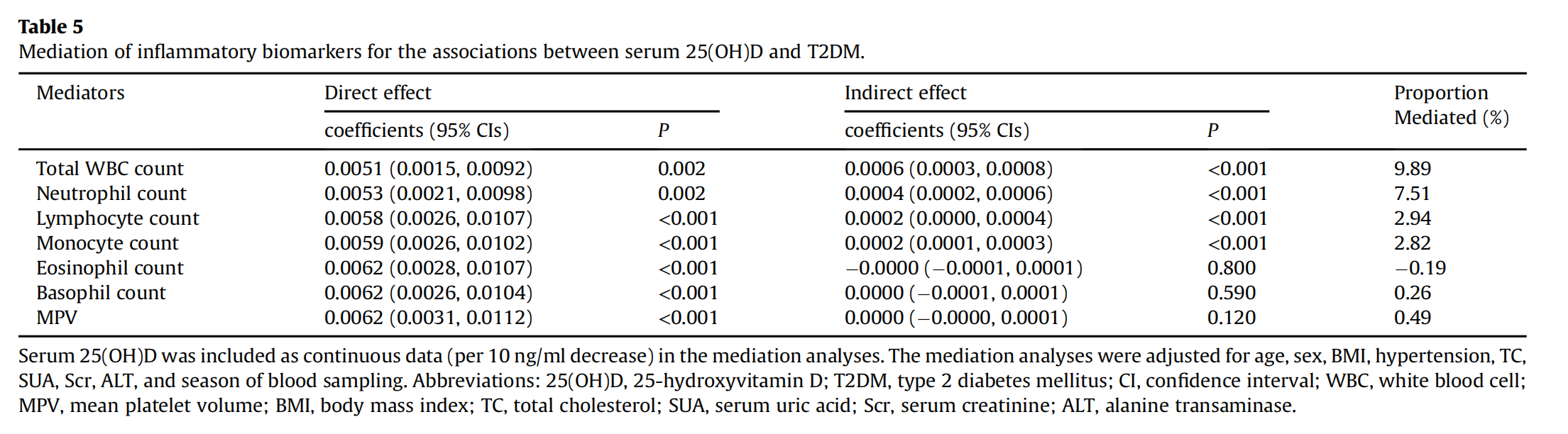
要怎么倒腾才能变成这样呢?需要强大的 R 编程能力才行。
不过,现在可以用 本软件 一键免编程直接生成这样的表格:
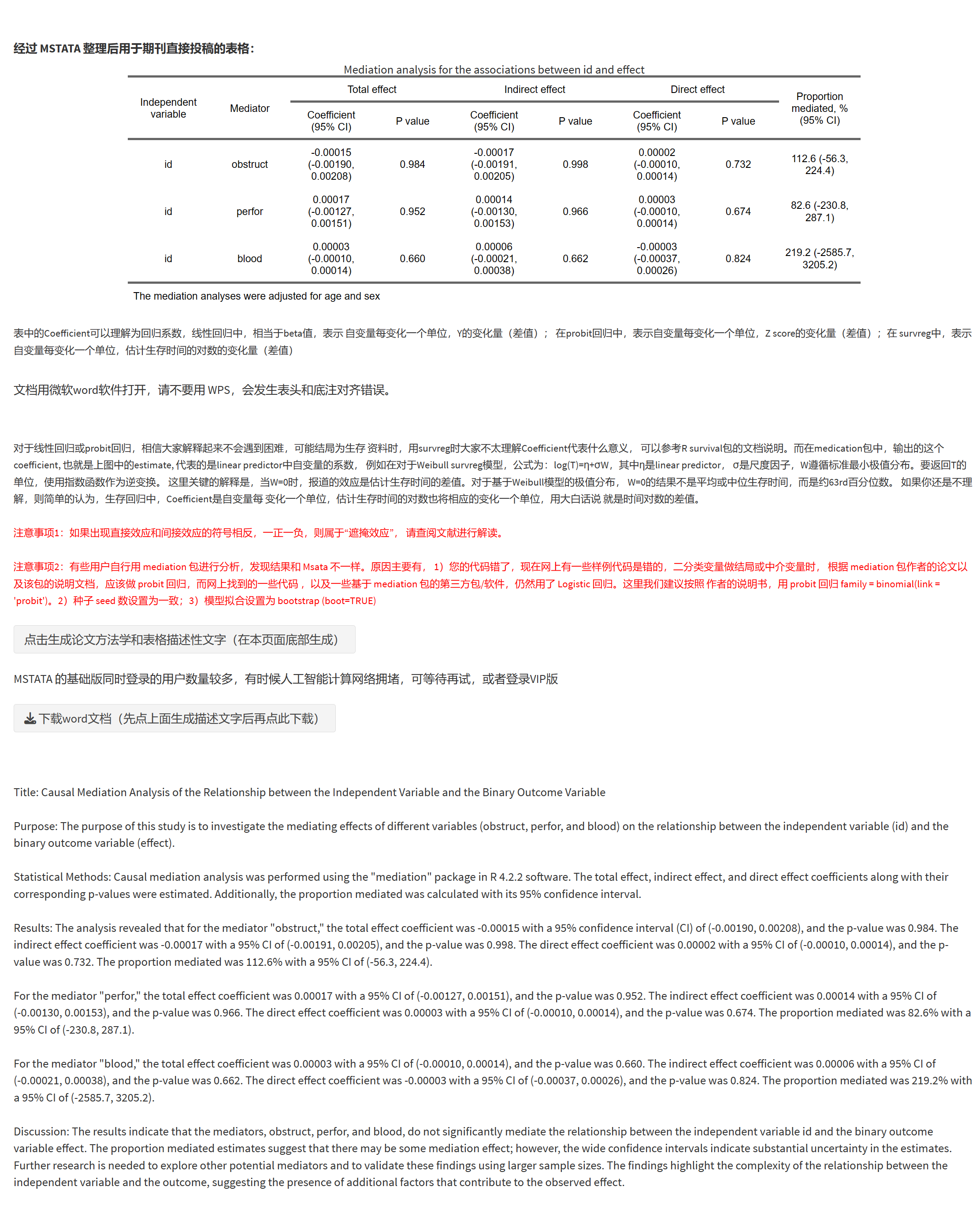
5.14.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:

本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,影响因素变量和结局变量,影响因素和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, status, time, occurrence在本例中是结局变量。
影响因素变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
生存型结局变量
需要用两个变量组合来表示,如本例中的status和time。
status代表患者在研究结束时的状态,在本工具中只能取0和1两个数字,不要用字符文本,否则会出错。0 代表没观察到事件发生(如没死或者失访),1 代表观察到了事件发生(如已经死亡且录入了死亡日期)。
time代表从开始日期(开始日期的定义由你的研究目的决定,如随机对照研究往往取随机化入组的那一天为开始日期,而观察性研究可以取首次诊断日期或首次治疗日期等等根据研究目的而定)到结局日期的时间差。当status=1时,结局日期为发生事件(如死亡)的日期,当status=0时,结局日期为最后一次活着的日期(如研究结束日,或随后一次随访日)。
总之,time是一个数值型变量,您需要填入患者从开始到死亡或者随后一次随访时,一共活着的天数。如time为56,status为1时代表患者从开始到死亡活了56天;当time为56,status为0时代表患者没观察到死亡,从开始到最后一次随访,活了56天。
准备数据时,time填入一个非负的整数,status填入0或1,time和status都不能为空,每个患者都必须填入数字。time或status不确定(缺失)时,该患者最好不要放入本数据库。
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
分数型结局变量
当结局变量为一个分数,如发病率、患病率、受精率等,结局包含一个分子和一个分母。如要研究全国各地疾病患病率的影响因素时,按照每个地区一行来准备数据,分子和分母设置成两个变量(列),如分子为患病人数,分母为地区人口数。
准备数据的规则是:分子和分母都是非负整数,不允许填入负数,也不允许填入小数,分子的数值不能大于分母。
5.14.2 进入模块
接下来我们进入模块,点击软件顶部菜单的“因果推断”,然后点击“因果中介效应(mediation包,支持连续性/二分类/有序分类/生存资料)” 进入模块。
本软件 做因果中介分析的界面如下:
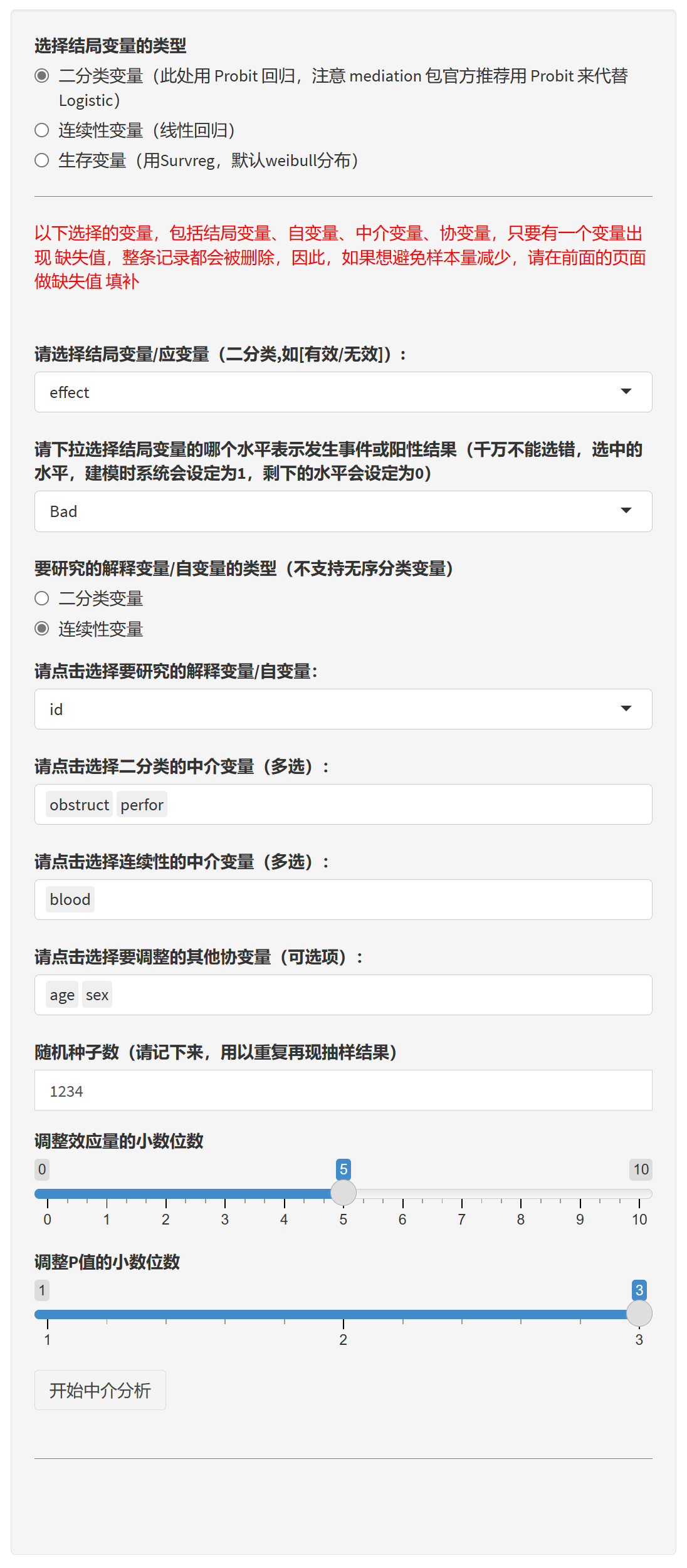
5.14.3 分析步骤
1. 选择结局变量的类型
在主界面上,您将首先看到一个名为”选择结局变量的类型”的选项。
您可以选择以下三种类型之一:
二分类变量(此处用 Probit 回归)
连续性变量(线性回归)
生存变量(用Survreg,默认weibull分布)
2. 选择结局变量/应变量
根据您在第一步选择的结局变量类型,软件将为您提供相应的变量选择。
请从下拉菜单中选择一个适当的结局变量。
3. 选择解释变量/自变量的类型
在”要研究的解释变量/自变量的类型”部分,选择您的自变量类型。
您可以选择二分类变量或连续性变量。
4. 选择解释变量/自变量
- 根据您选择的自变量类型,从下拉菜单中选择一个适当的自变量。
5. 选择中介变量的类型
在”选择中介变量(mediator)的类型”部分,选择您的中介变量类型。
您可以选择二分类变量或连续性变量。
6. 选择中介变量
- 根据您选择的中介变量类型,从下拉菜单中选择一个适当的中介变量。
7. 选择其他协变量(可选)
如果您希望在分析中考虑其他协变量,请从提供的列表中选择。
您可以选择多个协变量。
8. 调整回归系数和P值的小数位数
- 使用滑块调整回归系数和P值的小数位数,以满足您的需求。
9. 输入随机种子数
为了确保分析的再现性,请输入一个随机种子数。
记录这个数字,以便将来再次使用。
10. 开始中介分析
确保您已经完成了所有必要的选择和输入。
点击”开始中介分析”按钮,软件将开始进行中介分析,并为您提供结果。
生成word文档,包括目的,方法,结果和结论等都写好了: