Chapter 9 按统计学分类模块
9.1 两组独立样本 T 检验/秩和检验
本节说明如何在 本软件 中完成两组独立样本均值差异检验(Student/Welch t 检验)与秩和检验(Mann–Whitney U),并导出 Word/TXT 报告。本文仅涵盖建模与出表,不再复述数据准备流程。
适用于“两组互不重叠的受试者”(独立样本),例如:男性 vs 女性、新方案组 vs 对照组等。不适用于:同一人治疗前后(配对/重复测量)、三组及以上(ANOVA/非参扩展),或二分类结局(卡方/费舍尔)。
9.1.1 背景与方法小百科(必读)
- Student’s t 检验:比较两组均值是否不同;前提是各组近似正态且方差相等。样本量稍大时对偏离正态较稳健。
医学例子:新药 vs 标准治疗的降压幅度(mmHg)是否不同。 - Welch’s t 检验:t 检验的改良版,不要求方差相等(对方差不齐更稳健)。现实研究里优先推荐。
医学例子:两种术式后住院天数均值比较(两组方差差异往往明显)。 - Mann–Whitney U(秩和检验):不依赖正态性,比较两组总体分布是否有系统性差异(常被简化理解为“中位数差异”,但严格说是分布的差异)。
医学例子:疼痛评分(0–10)常偏态/有极端值,用秩和检验更稳妥。 - 均值差(MD):两组均值之差(组1−组2),配合95% 置信区间一起报告更完整。
- 效应量 Cohen’s d:把“均值差”除以“组内标准差的综合”,无量纲,便于不同量纲比较(约 0.2/0.5/0.8 分别常被称为小/中/大效应)。
- Shapiro–Wilk 正态性检验:p 值小提示偏离正态;大样本下对微小偏离也很敏感,需结合 Q–Q 图。
- Q–Q 图:判断正态性最直观的图;点大致落在直线附近→近似正态。
- Levene 方差齐性检验:检测两组方差是否相等;方差不齐时用 Welch’s t。
- 贝叶斯因子(BF10):>3 支持“有差异”、<1/3 支持“无差异”,介于中间为不确定;与 p 值互补。
小贴士
- Welch’s t 在实际研究里很常用,因为“方差齐性”常不满足。
- 秩和检验更稳健,但它检验的是分布差异;若两组分布形状/离散程度不同,不能简单等同“中位数差异”。
9.1.2 数据准备
整洁数据格式(每行一名受试者):至少包含 1 列连续型结局(Y)和 1 列二分类分组变量(Group)。两列都应在 “定义字段” 中设定为正确类型:Y 为 numeric/integer,Group 为 factor(恰好两类)。
9.1.2.1 必要字段
id(可选):受试者编号,便于核查;group:二分类分组(如 Treatment / Control,或 Male / Female);y:连续结局(如 血压下降值 mmHg、CRP、住院天数 等)。
不要把两组的 Y 放在两列(如
y_treat与y_ctrl),那是“配对/重复测量”的宽表结构,不适用于独立样本检验。本模块需要“一列 Y + 一列 Group”。
9.1.2.2 示例数据表(每行一人)
| id | group | y (SBP reduction, mmHg) |
|---|---|---|
| 1 | Treatment | 12.5 |
| 2 | Treatment | 8.0 |
| 3 | Treatment | 15.2 |
| 4 | Control | 6.1 |
| 5 | Control | 9.3 |
| 6 | Control | 2.7 |
| … | … | … |
准备要点与小贴士
- 类型:Y 需是 numeric;Group 设为 factor 且只有两类。若 Group 目前有 3 类及以上,请在 “定义字段/调整因子顺序” 合并为两类。
- 取值丰富度:去除缺失后,Y 在每组建议至少有 ≥ 3 个不同取值。
- 缺失:允许缺失。分析时可选按变量剔除或整行剔除(见“缺失值处理”)。
- 极端值:如存在明显异常或右偏,建议同时报告 Mann–Whitney U 结果作稳健性参考。
- 单位一致:确保同一指标量纲一致(如都为 mmHg)。
9.1.4 选择变量
因变量 Y(连续型)
在 “选择因变量或结局变量 Y” 下拉框中选择。- 必须是
numeric/integer,且去缺失后≥3 个不同取值。
- 若未出现,请回到 “定义字段” 将其设置为
numeric。
名词解释:连续型变量 是可以细分到任意精度的数,如血压、肌酐、住院天数等。
- 必须是
分组变量(两组)
在 “选择分组变量(二分类变量)” 选择恰好两类的变量。- 如果当前是 3 类及以上,请在 “定义字段/调整因子顺序” 合并为两类。
名词解释:二分类变量 是仅有两类的类别变量,如“治疗/对照”“男/女”。
提示:若要改变“组1/组2”的先后顺序,请到 “调整因子顺序” 拖拽分组变量的水平顺序。
9.1.5 检查前提假设(可选但推荐)
在 “适用条件判断” 勾选需要的检验:
- Shapiro–Wilk 正态性检验(默认开):判断两组数据是否近似正态。
- Q–Q 图:可视化正态性(默认开,与上项联动)。
- Levene 方差齐性检验:判断两组方差是否近似相等。
怎么用这些结论?
- 正态 + 方差齐:可用 Student’s t(或直接用更稳健的 Welch’s t)。
- 正态 + 方差不齐:优先用 Welch’s t。
- 明显偏态/极端值:可用 Mann–Whitney U 做主分析/敏感性分析。
9.1.6 选择统计方法(可多选并行出结果)
- Student’s t test:方差齐时的 t 检验。
- Welch’s t test:不要求方差齐;现实里更稳健,优先推荐。
- Mann–Whitney U(秩和检验):正态性不佳或有极端值时使用。
- 贝叶斯因子:提供与 p 值互补的“证据强度”。
医学里的直观例子
- t/Welch:比较两治疗组的舒张压下降值(mmHg)。
- 秩和:比较两术式的住院天数(常偏态)。
- 贝叶斯因子:当 p≈0.06 时,用 BF 判断“无差异”的证据是否也很强。
###(可选)对因变量做正态性变换
当 Y 全为正数 时,会出现下列选项:
- 不转换(默认)
- 对数转换(log):适合“倍数变化”的指标(如 CRP、乳酸)。
- 平方根转换(√):适合轻度右偏的数据。
- 倒数转换(1/x):适合极端右偏,但解释较不直观。
解读提醒:
- log 变换后的“均值差”近似表示几何均值之比的对数;必要时在结果里加一句解释。
- 变换仅为满足模型近似前提;若变换前后结论一致,可在文中说明“敏感性分析一致”。
9.1.7 假设检验方向
在 “假设检验类型” 选择:
- 组1 ≠ 组2(双侧,默认)
- 组1 > 组2 或 组1 < 组2(单侧)
名词解释:
- 双侧检验:只要两组不一样就算显著。
- 单侧检验:仅在“有明确且事先约定的方向性假设”时使用(如新药只可能更强)。
“组1/组2”由分组水平顺序决定;方向弄反可在“调整因子顺序”或此处重选方向。
9.1.8 显示统计量与区间
均值差(MD) 与 95% 置信区间(可改置信水平)。
> 置信区间:若多次重复同样研究,95% 的此类区间会覆盖真实均值差。区间不跨 0 → 与双侧检验显著一致。效应量(Cohen’s d) 与区间(可选):
> Cohen’s d = 均值差 ÷ 组内标准差的综合;0.2/0.5/0.8 常对应小/中/大效应,仅供粗略参考。
9.1.9 缺失值处理
- 每个因变量单独剔除缺失(默认):保证尽可能多的有效样本,但不同结果的样本量可能不同。
- 整行有缺失就剔除:所有分析样本量一致,但丢失信息更快。
医学建议:优先默认策略;若担心偏倚,可在数据准备模块做缺失填补后再分析。
9.1.10 描述性统计与图
- 描述性统计表:输出两组的均值/SD 或中位数/IQR(由底层自动选择/展示)。
- 描述性统计图:默认开启,可调 图像宽度/高度;图下方提供下载按钮(PNG/PPT/PDF)。
9.1.11 一键运行
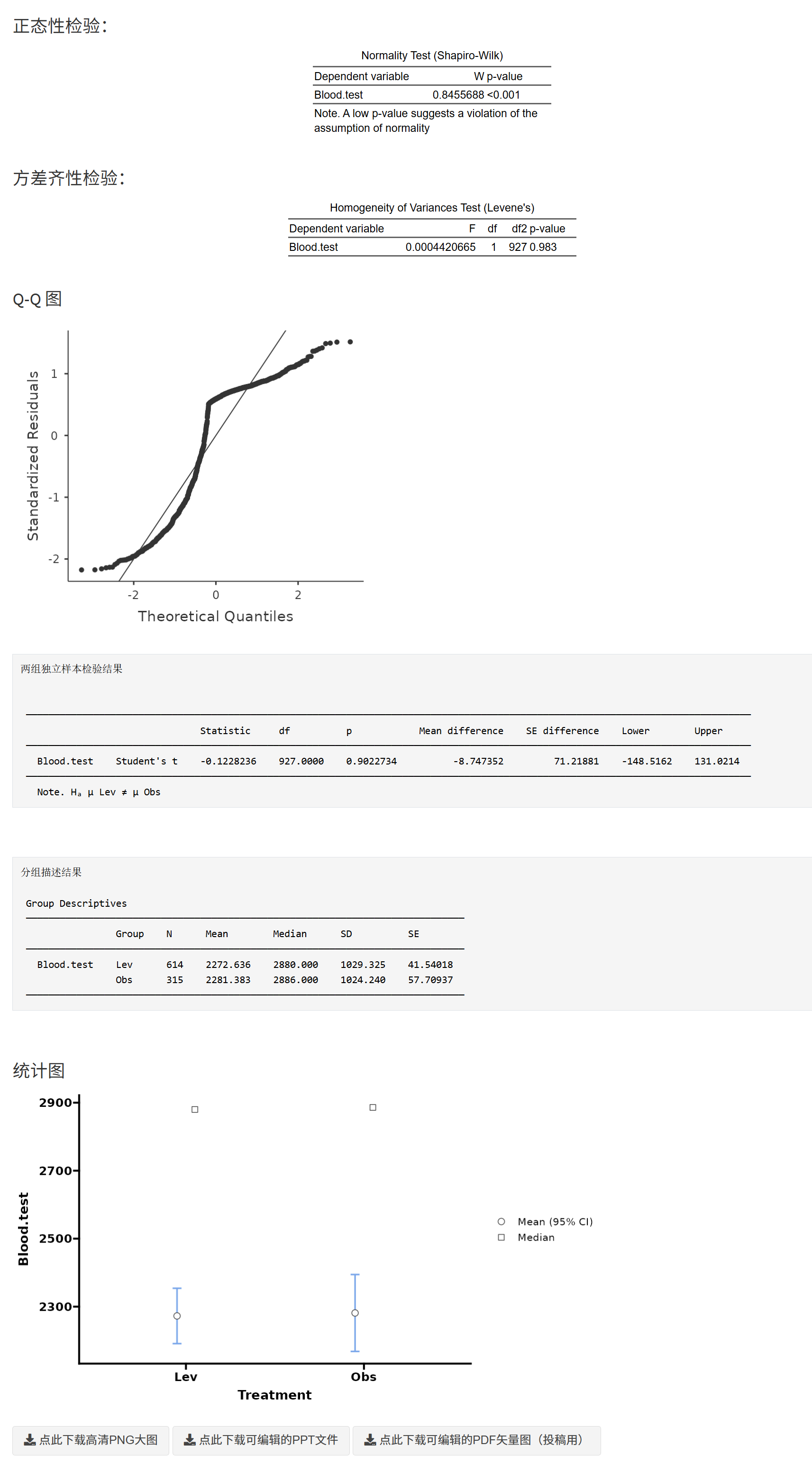
点击 “开始进行两组独立样本检验分析”。页面将依次显示:
- 正态性检验表(Shapiro–Wilk)
- 方差齐性检验表(Levene)
- Q–Q 图(若开启)
- 主检验结果(t/秩和/贝叶斯):t 值/自由度、p 值、均值差(及 CI)、可选的效应量
- 分组描述结果(文本表)
- 描述性统计图
解读建议
- Welch’s t 对方差不齐更稳健;常作为主要结果。
- 若正态性/方差齐性明显违背,Mann–Whitney U 可作为主结果或敏感性分析。
- 始终伴随报告效应量与置信区间,避免只报 p 值。
9.1.12 导出结果
切换到 “下载Word报告” 页签:
下载 Word 文档:包含
- 正态性检验表、2) 方差齐性检验表、3) Q–Q 图、4) 描述性统计图。
- 请用 Microsoft Word 打开(不要用 WPS,可能样式不兼容)。
- 正态性检验表、2) 方差齐性检验表、3) Q–Q 图、4) 描述性统计图。
下载 TXT 文本:包含
- 两组检验主结果表与分组描述结果(纯文本,便于粘贴至邮件/文稿)。
高分辨率图片:在图下方用图片下载按钮(PNG/PPT/PDF)。
9.1.13 常见问题与排查
- 因变量未出现在下拉框:回到 “定义字段” 将其设为
numeric,并确保去缺失后有 ≥3 个不同取值。
- 分组变量不是两类:请在 “定义字段/调整因子顺序” 合并水平,使其恰为两类。
- p 值或区间异常巨大/为 NA:多因极端值或样本极小;检查离群值,或改用秩和检验。
- Q–Q 图未显示:确认已勾选 Shapiro–Wilk(取消该项也不会生成 Q–Q 图)。
- 单侧检验方向弄反:检查“组1/组2”的水平顺序或更换单侧方向,再次运行。
- Word 排版错乱:使用 Microsoft Word 打开;如仍异常,减少一次性插入的图片尺寸后重试。
9.2 两组配对样本 T 检验/秩和检验
本节说明如何在 本软件 中完成两组配对样本的均值差异检验(配对 t 检验)与配对的非参数检验(Wilcoxon 符号秩和检验),并导出 Word/TXT 报告。仅涵盖建模与出表,不再复述数据准备流程。文中对统计名词都做了入门解释,适合统计小白快速上手。
9.2.1 背景与原理(先懂再做)
什么是“配对样本”?
同一受试者在两个时间点/两侧器官/两种处理下的两次测量,一人两值,两值彼此成对。例如术前/术后血压、治疗前后某生物标志物、左/右眼眼压。同一人的两次测量高度相关,不能当作独立样本处理。配对 t 检验(Student’s paired t)
把每个受试者的“差值” \(d = \text{测量1} - \text{测量2}\) 当作一列新数据,检验差值的平均数是否为 0。
适用条件:差值 \(d\) 近似正态分布。优势:对小样本也常见,结果易解释(给出均值差 MD及其置信区间)。Wilcoxon 符号秩和检验(配对的非参数法)
不要求正态。对差值的绝对值做秩次排序,再根据正负号加总,检验“中位差是否为 0”。
适用场景:差值偏态/有极端值时更稳妥。解释为中位数层面的差异。贝叶斯因子(Bayes factor, BF)
量化数据支持“有差异”还是“无差异”。常用阈值:
BF10 > 3倾向支持存在差异;BF10 < 1/3倾向支持无差异;中间区域为不确定。需要给定一个先验宽度(默认 0.707)。医学研究中的常见例子
- 抗高血压药物前后收缩压(同一人两次)。
- 手术前后炎症指标 CRP。
- 左/右肾皮质厚度(同一人左右侧比较)。
这些都应使用配对方法,而不是独立样本方法。
- 抗高血压药物前后收缩压(同一人两次)。
9.2.2 数据准备
数据必须是“宽表”(wide format):每位受试者占一行,有两列分别存放两次测量值。两列都应为数值型(numeric/integer),去除缺失后至少各有 3 个不同取值。
9.2.2.1 必要字段
id(可选):受试者编号或样本 ID(便于自查)。measure_1:第一次测量(如“基线”/“用药前”)。measure_2:第二次测量(如“末次随访”/“用药后”)。
若你的原始数据是“长表”(如列有
id/time/value),请先在外部软件或 R 中转换为宽表,使两个测量各占一列,再导入 本软件。
9.2.2.2 示例数据表(宽表)
| id | measure_1 (Pre) | measure_2 (Post) |
|---|---|---|
| 1 | 142.0 | 134.0 |
| 2 | 150.5 | 141.0 |
| 3 | 138.0 | 139.5 |
| 4 | 160.0 | 148.0 |
| 5 | 147.5 | 143.0 |
| … | … | … |
准备要点与小贴士 - 变量类型:两列测量都应在 “定义字段” 中设为 numeric;若显示为 factor/character,请更改为 numeric。
- 缺失:允许有缺失。分析时可选择按变量剔除或整行剔除(见后文“缺失值处理”)。
- 极端值:若差值分布偏态/有极端值,建议同时报告 Wilcoxon 结果作稳健性参考。
- 同一单位:两次测量必须同量纲、同单位(如都为 mmHg)。
9.2.4 选择变量(两列测量值一一对应)
- 第一个测量值(测量1)
在 “选择第一个测量值(需在前页面设置成 numeric)” 选择。要求:数值型,去缺失后至少 3 个不同取值。
- 第二个测量值(测量2)
在 “选择第二个测量值(需在前页面设置成 numeric)” 选择。
> 重要:两列必须来自同一批受试者且顺序一致(第 i 行的两值属于同一人)。如存在配对错位,结果将失真。
小贴士:如果变量未出现在下拉框,请回到 “定义字段” 把该列设为
numeric并应用更改。
9.2.5 检查前提假设(推荐)
- Shapiro–Wilk 正态性检验(默认开)
检验的是差值 \(d\) 是否近似正态(界面中自动完成差值并检验)。
- Q–Q 图(默认开)
可视化差值 \(d\) 的正态性:点越贴近对角线越接近正态。
说明:若取消 Shapiro–Wilk,系统也不会生成 Q–Q 图(与界面勾选保持一致)。
9.2.6 选择统计方法(可多选并行出结果)
- Student’s t test(配对 t 检验):差值近似正态时的首选。
- Wilcoxon signed rank tests(符号秩和检验):差值不正态/有极端值时更稳健。
- 贝叶斯因子法:可选。默认先验 0.707(可在 0.01–2 之间调整)。
9.2.7 假设检验方向(一定要对齐“谁减谁”)
在 “假设检验类型” 选择:
- 测量值1 ≠ 测量值2(双侧,默认)
- 测量值1 > 测量值2 或 测量值1 < 测量值2(单侧)
方向如何理解?系统以“测量1 − 测量2”构造差值:
- 选择“测量1 > 测量2”即假设 差值均值 > 0;
- 选择“测量1 < 测量2”即假设 差值均值 < 0。
若结果方向和期望相反,可对调两列或改选相反方向。
9.2.8 显示哪些统计量
- 均值差(MD) 与 置信区间(默认 95%)
MD = 平均(测量1 − 测量2)。区间不跨 0 常提示差异显著。
- 效应量(Effect size) 与置信区间(可选)
对配对 t,系统给出类似 Cohen’s d 的标准化差值(等于差值均值 ÷ 差值标准差)。
粗略阈值:0.2(小)、0.5(中)、0.8(大)。
9.2.10 描述性统计与图(便于展示)
- 描述性统计表:两次测量各自的均值/SD 或中位数/IQR(由底层函数自动选择/展示)。
- 描述性统计图:默认开启,可调 图像宽度/高度。
图下方提供图片下载(PNG/PPT/PDF),便于插入幻灯或稿件。
9.2.11 一键运行
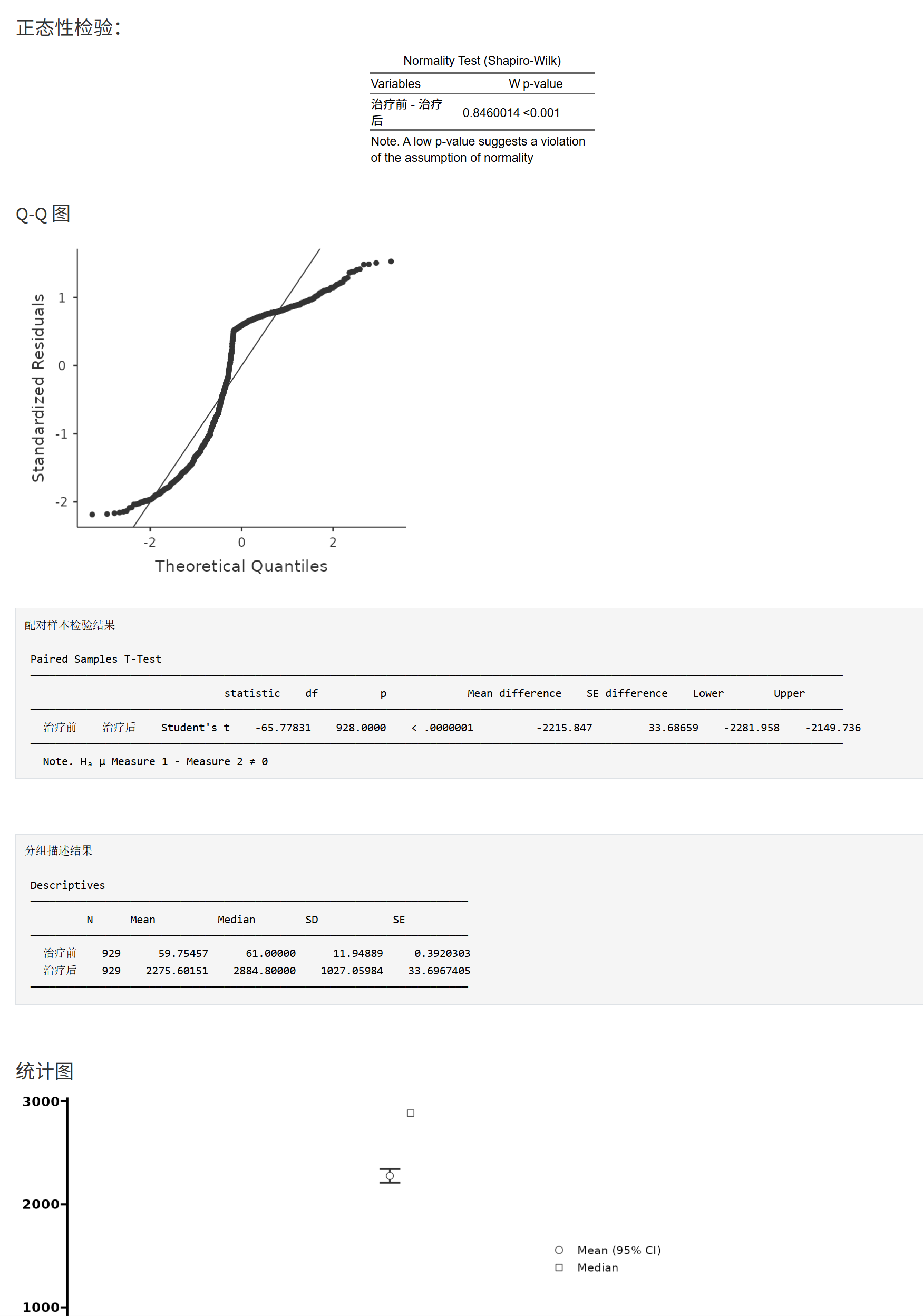
点击 “开始进行两组独立样本检验分析”(按钮名称沿用界面文案)。完成后将依次看到:
- 正态性检验表(Shapiro–Wilk):针对差值 \(d\)。
- Q–Q 图(若开启):目测差值是否近似正态。
- 主检验结果(根据你勾选的方法并行展示):
- t 值/自由度(df)、p 值、均值差(MD)及其 CI;
- 效应量(Cohen’s d)及其 CI(如勾选);
- 贝叶斯因子(BF)(如勾选),并可据阈值解读;
- t 值/自由度(df)、p 值、均值差(MD)及其 CI;
- 分组描述结果(文本表)
- 描述性统计图(可下载为 PNG/PPT/PDF)
解读建议
- 若差值近似正态,优先报告配对 t;如偏离明显,报告 Wilcoxon 作为敏感性或主结果。
- 同时报告 MD 与其 CI、效应量,比只报 p 值更完整。
- 若临床上更关注“术后是否下降”,请采用单侧方向并在方法中说明依据。
9.2.12 导出结果
切换 “下载Word报告” 页签可导出:
- Word 文档(推荐用 Microsoft Word 打开,勿用 WPS 以免格式错乱),包含:
- 正态性检验表 2) Q–Q 图 3) 描述性统计图。
- 正态性检验表 2) Q–Q 图 3) 描述性统计图。
- TXT 文本:包含主检验结果与描述性统计(文本),便于复制粘贴到论文草稿。
高分辨率图片:建议用图下方的图片下载按钮(PNG/PPT/PDF)。
9.2.13 医学写作示例(可直接改词套用)
- “我们采用配对 t 检验比较治疗前后 Y 值。差值(前−后)的均值差为 MD=…(95% CI …),t(df)=…,p=…;效应量 d=…(95% CI …)。结果提示治疗后Y显著下降/无显著变化。”
- “作为稳健性分析,我们使用Wilcoxon 符号秩和检验,得到 V=…,p=…,结论与配对 t 一致/不同。”
- “若采用单侧假设(前 > 后),结论仍然成立/不成立(p=…),与研究假设一致/不一致。”
9.2.14 常见问题与排查
- 两列样本数不同或顺序不一致
必须一人一行、两列一一对应;如有错位,请按受试者 ID 对齐或重建数据表。
- 变量没出现在下拉框
回到 “定义字段” 将两列设置为numeric,并点击应用更改。
- Q–Q 图不显示
请确认已勾选 Shapiro–Wilk 正态性检验;否则系统不会生成 Q–Q 图。
- 效应量或区间异常
多见于样本过小或差值极端;可查看箱线图/原始点图,必要时使用 Wilcoxon 并在文中说明理由。
- 方向与期望相反
记住系统计算的是“测量1 − 测量2”。可在“假设检验类型”选择相反方向,或交换两列后重跑。
- Word 格式错乱
使用 Microsoft Word 打开;若仍异常,降低图尺寸或数量后重导。
9.3 单样本 T 检验/秩和检验
本节说明如何在 本软件 中完成单一样本与某个理论检验值(基准值)的比较:包括 单样本 t 检验 与 单样本 Wilcoxon 符号秩和检验,并导出 Word/TXT 报告。适用于“一组受试者”的某项连续指标是否高于/低于/不同于既定标准(如指南阈值、历史对照均值)。
9.3.1 背景与方法小百科(必读)
单样本 t 检验(Student’s one-sample t)
用于判断样本均值是否与检验值(μ₀)不同;要求该指标在总体上近似正态。
医学例子:某降压药试验组的舒张压下降幅度是否与“临床目标 5 mmHg”不同。单样本 Wilcoxon 符号秩和检验(Wilcoxon signed-rank, one-sample)
非参数方法,不要求正态,检验总体分布的中位数是否等于检验值(严格地说是对称分布下的“位置差异”)。
医学例子:疼痛评分(0–10)是否显著低于“可耐受阈值 4 分”(偏态常见)。检验值(Test value, μ₀)
你要对照的基准:指南阈值、历史均值、理论值(如 0)。单样本 t 的均值差 = 样本均值 − μ₀。Shapiro–Wilk 正态性检验 & Q–Q 图
用于评估“近似正态”前提:p 值小提示偏离正态;大样本对轻微偏离也很敏感,需结合 Q–Q 图。效应量(Cohen’s d)
= (样本均值 − μ₀) / 样本标准差,无量纲,≈0.2/0.5/0.8 常对应小/中/大效应(仅作粗略参考)。贝叶斯因子(BF₁₀)
表示“有差异”相对“无差异”的证据强度:>3 支持有差异,<1/3 支持无差异,中间为不确定。
9.3.2 数据准备
数据应为“宽表”(wide format):每位受试者占一行,目标变量仅一列,为数值型(numeric/integer),去除缺失后至少 3 个不同取值。
9.3.4 选择变量与检验值
- 选择因变量(连续型)
在 “选择因变量(需在前页面设置成 numeric)” 下拉框中选择目标变量。- 必须是
numeric/integer,且去缺失后 ≥ 3 个不同取值。
- 未出现时,请回到 “定义字段” 更改类型。
- 必须是
- 输入检验值(μ₀)
在 “输入检验值” 中填入你要对照的基准值(默认 0)。- 例:检验“平均 SBP 是否不同于 140 mmHg”,则输入 140。
- 例:检验“平均变化量是否不同于 0”,则输入 0。
- 例:检验“平均 SBP 是否不同于 140 mmHg”,则输入 140。
名词解释:均值差(MD) = 样本均值 − 检验值。置信区间不跨 0 → 与双侧检验“显著”一致。
9.3.5 检查前提假设(可选但推荐)
在 “适用条件判断” 勾选需要的检验:
- Shapiro–Wilk 正态性检验(默认开):评估“近似正态”。
- Q–Q 图:可视化正态性(默认开,与上项联动)。
怎么用?
- 近似正态:可用 t 检验(常规报告)。
- 明显偏态/极端值:同时报告 Wilcoxon(稳健)。
9.3.6 选择统计方法(可多选并行出结果)
- Student’s t test(单样本 t):基于均值,需“近似正态”。
- Wilcoxon signed-rank(单样本):基于秩与符号,更稳健。
- 贝叶斯因子:提供与 p 值互补的证据强度(默认先验 r = 0.707,可调 0.01–2)。
医学里的直观例子
- t 检验:平均 CRP 是否不同于 10 mg/L(CRP 近似正态或样本量中等偏大)。
- Wilcoxon:平均疼痛评分是否低于 4 分(评分常偏态)。
- BF:当 p≈0.06 时,用 BF 判断“无差异”的证据是否同样强。
9.3.7 假设检验方向
在 “假设检验类型” 选择:
- ≠ 检验值(双侧,默认)
- > 检验值 或 < 检验值(单侧)
名词解释:
- 双侧检验:只要“不同于”就算显著(更常用、也更稳妥)。
- 单侧检验:仅在事先有明确方向且与伦理/机制一致时使用(如“只关心是否高于阈值”)。
9.3.8 显示统计量与区间
均值差(MD) 与 95% 置信区间(可改置信水平)。
> 置信区间:若重复同样研究,95% 的此类区间会覆盖真实“均值差”。区间不跨 0 → 与双侧显著一致。效应量(Cohen’s d) 与区间(可选):
> d = (样本均值 − 检验值) / 样本 SD;0.2/0.5/0.8 ≈ 小/中/大效应,仅供粗略参考。
9.3.9 缺失值处理
- 每个因变量单独剔除缺失(默认):尽量保留样本,但不同结果的样本量可能不同。
- 整行有缺失就剔除:各输出的样本量一致,但信息损失更快。
建议:通常保留默认;如担心偏倚,可在数据准备模块先做缺失填补,再回来分析。
9.3.10 描述性统计与图
- 描述性统计表:显示均值/SD 或中位数/IQR(由底层自动选择/展示)。
- 描述性统计图:默认开启,可在界面调整图像宽度/高度。
- 图下方提供下载按钮(PNG/PPT/PDF),便于制图入稿。
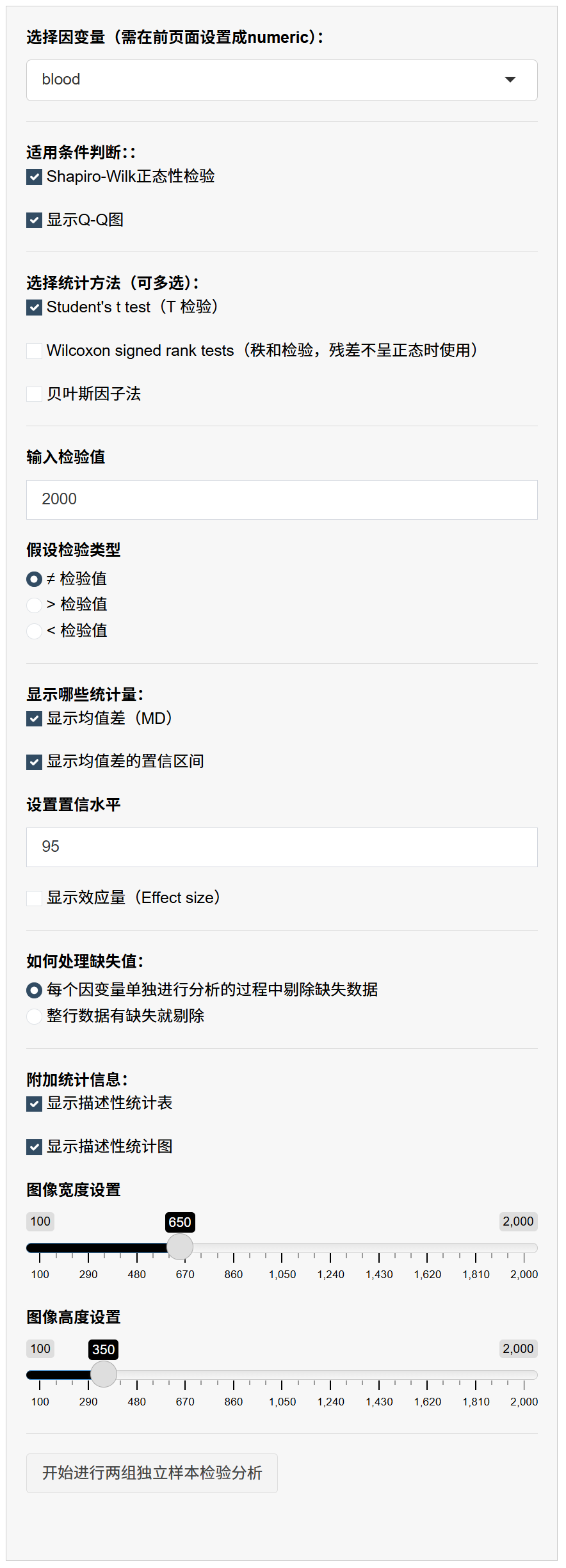
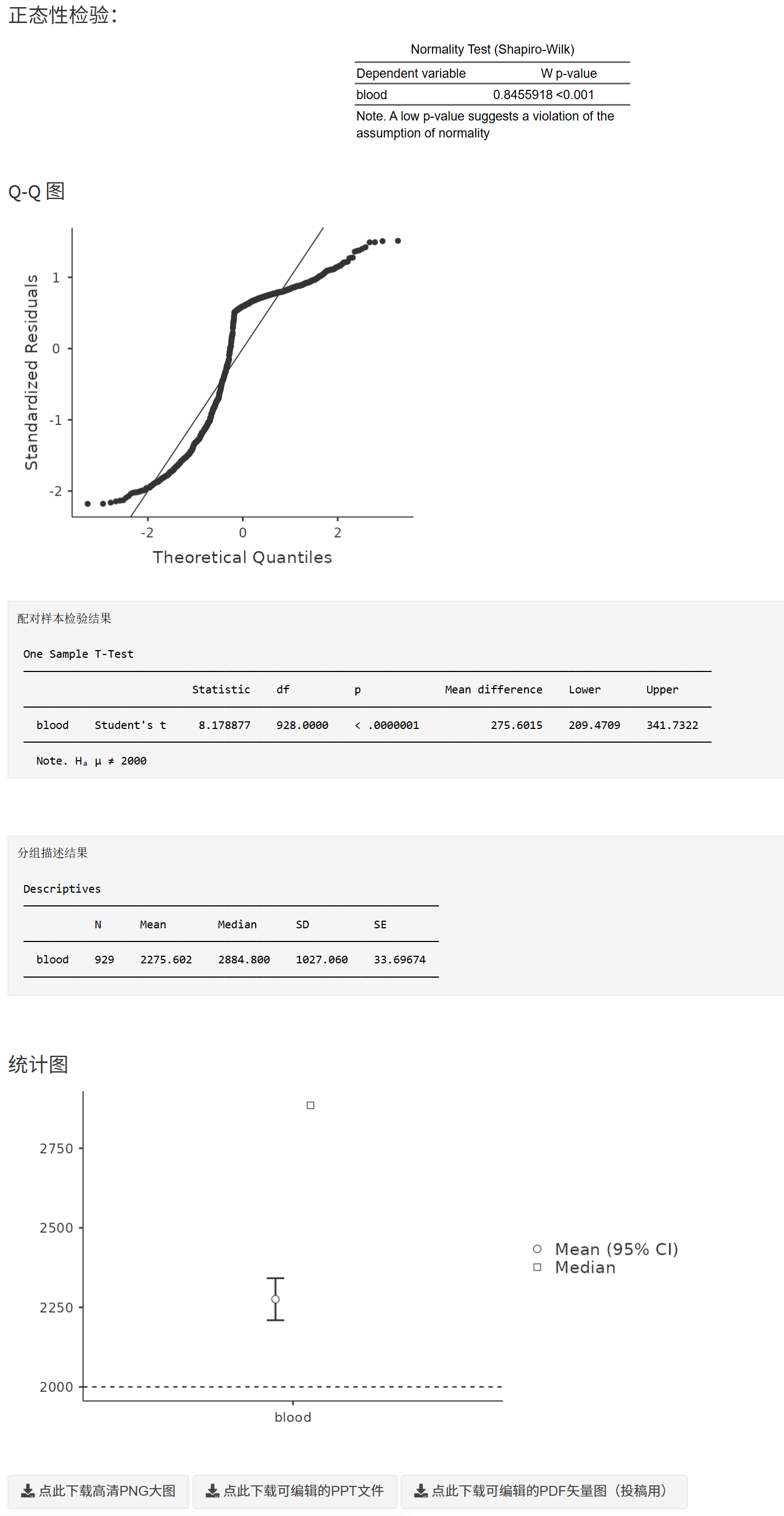
9.3.11 一键运行
点击 “开始进行两组独立样本检验分析”(按钮文字通用,此处为单样本)。页面将依次显示:
- 正态性检验表(Shapiro–Wilk)
- Q–Q 图(若开启)
- 主检验结果(t / Wilcoxon / 贝叶斯):t 值/自由度、p 值、均值差(及 CI)、可选的效应量
- 描述性统计表(文本)
- 描述性统计图(可下载)
解读建议
- 近似正态下可主要报告 t 检验;若偏态明显,补充 Wilcoxon 作为稳健性分析。
- 始终配合置信区间与效应量,避免只报 p 值。
- 样本量很大时,微小差异也可能显著;此时更应关注效应量与临床意义。
9.3.12 导出结果
切换到 “下载Word报告” 页签:
下载 Word 文档:包含
- 正态性检验表、2) Q–Q 图、3) 描述性统计图。
- 请用 Microsoft Word 打开(不要用 WPS,可能样式不兼容)。
- 正态性检验表、2) Q–Q 图、3) 描述性统计图。
下载 TXT 文本:包含
- 单样本检验主结果表与描述性统计(纯文本,便于粘贴至邮件/文稿)。
高分辨率图片:在图下方使用图片下载按钮(PNG/PPT/PDF)。
9.3.13 常见问题与排查
- 变量未出现在下拉框:回到 “定义字段” 将其设为
numeric,且去缺失后 ≥ 3 个不同取值。
- p 值或区间异常/为 NA:多因极端值或样本极小;请检查离群值,或同时报告 Wilcoxon。
- Q–Q 图未显示:确认已勾选 Shapiro–Wilk(取消该项也不会生成 Q–Q 图)。
- 单侧/双侧选择不当:仅在有事先方向假设时用单侧;否则使用双侧更稳妥。
- Word 排版错乱:使用 Microsoft Word 打开;若仍异常,减少一次性插入的图片尺寸后重试。
9.4 独立样本列联表分析(卡方检验、趋势检验等)
列联表(Contingency Table),又称交叉表、列联表分析,是用于表示两个或多个分类变量之间关系的表格。在医学研究中,列联表广泛应用于疾病与风险因素、治疗方法与疗效等方面的关联性分析。
例如,通过卡方检验(Chi-square test)评估吸烟是否与肺癌的发病率相关,或者通过趋势检验(Trend test)研究不同剂量药物治疗对疾病恢复的影响。
本软件为列联表分析提供了全面且强大的功能支持,以下是其主要功能介绍:
多种假设检验方法:本软件支持χ²检验、连续性校正χ²检验、似然比(Likelihood ratio)检验、Fisher’s 精确检验和Z检验等方法,以满足不同场景和数据类型的需求。
自定义假设检验类型:用户可以根据研究目的,自主选择双侧检验(two-tailed test)或单侧检验(one-tailed test)。
效应量估计:本软件可以计算比值比(Odds Ratio, OR)、对数比值比(Log OR)、相对危险度(Relative Risk, RR)、两组发生率差值(Risk Difference, RD)等效应量,并给出相应的置信区间。
设置置信水平:用户可以根据需要自行设定置信水平(Confidence Level),如95%或99%等。
计算列联系数:对于无序分类变量,本软件能计算φ系数(Phi coefficient)、Cramer’s V系数等列联系数;对于有序分类变量,本软件支持计算Gamma系数、Kendall’s Tau-b系数等趋势检验指标。
Mantel-Haenszel趋势检验:本软件支持Mantel-Haenszel趋势检验,用于评估具有有序分类变量的列联表中的趋势关系。
选择分层因素,自动分层分析。
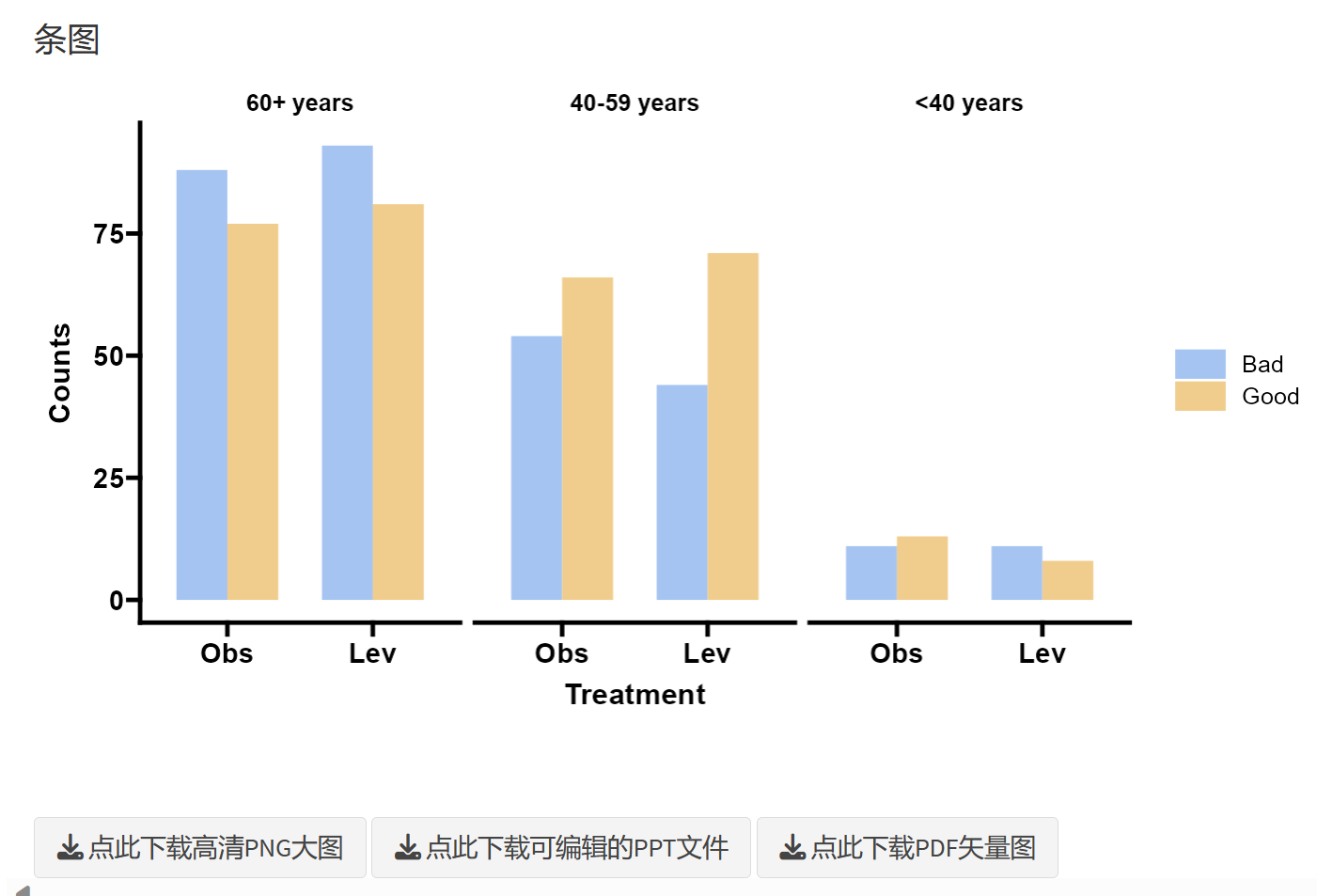
可视化分析:本软件能绘制列联表的统计条图,直观地展示分类变量之间的关系。

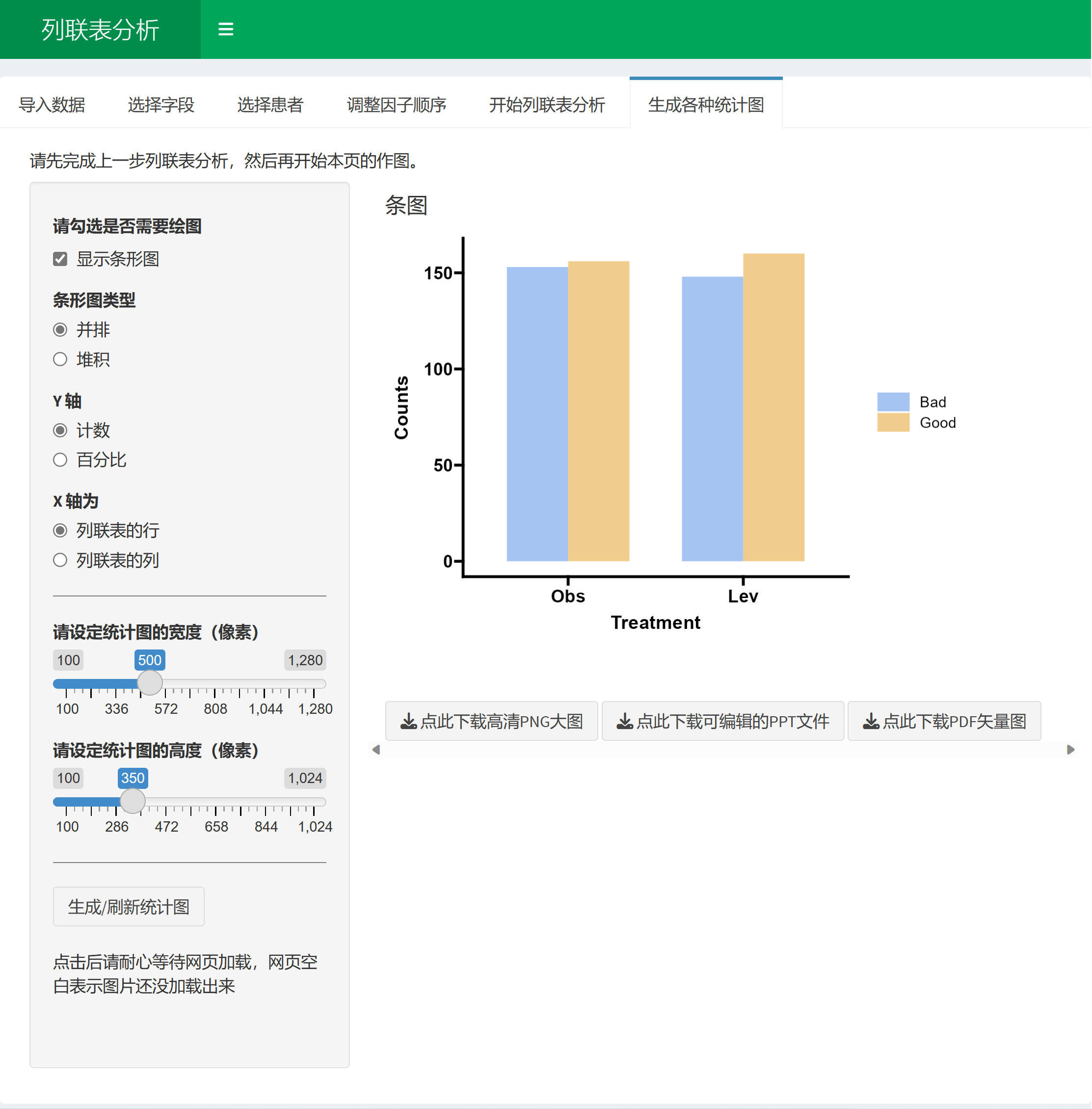
9.4.1 准备数据
到”导入数据”页面下载示例数据看一下:
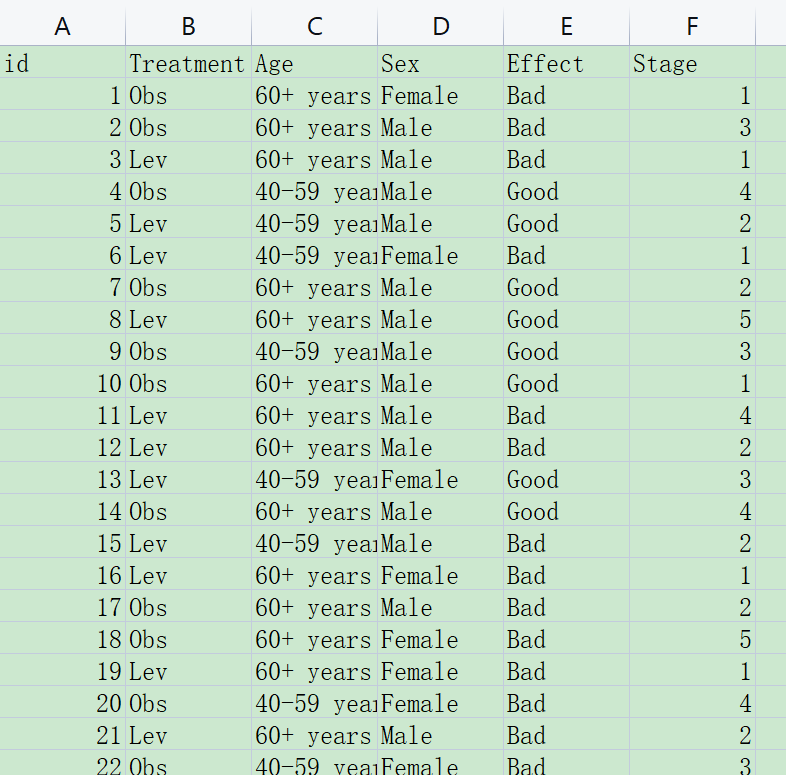
Treatment, Age, Sex 都是分类变量,代表分组因素
Effect是疗效,也是分类变量
Stage 是数字,但是不是连续性变量,我们认为是一个分类,但是每个分类之间有数量关系,所以这里是一个有序分类变量,导入本软件后,需要设置为factor,后续在趋势检验中有用。
如果没有原始的个体数据,只有四格表或者列联表的频数:
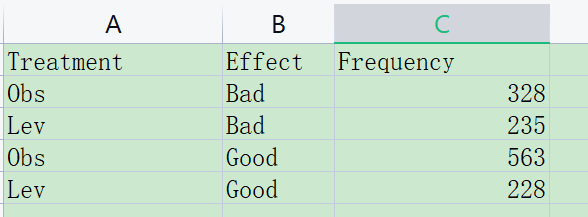
则按照这样的格式准备数据,多出一个变量Frequency表示频次,导入软件后将其设置为频次或权重即可。
9.4.4 列联表统计的参数
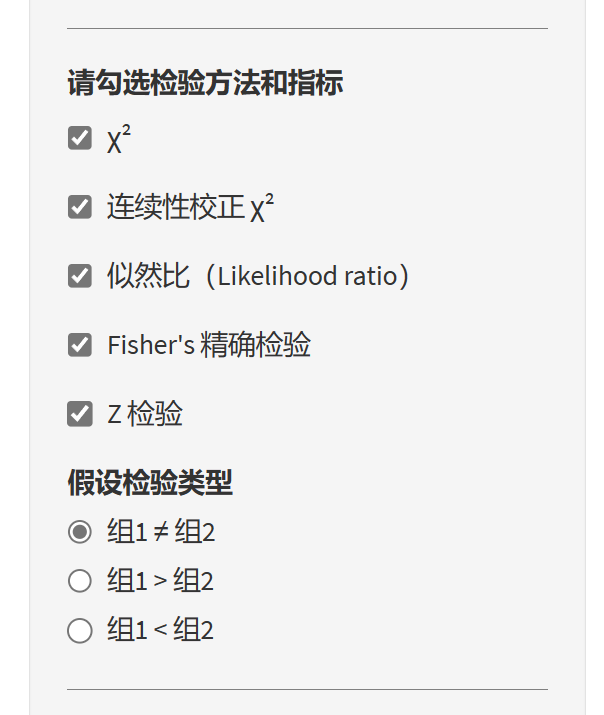
请勾选需要计算的参数,说明如下:
χ²(卡方检验,Chi-square test)
定义:卡方检验是一种非参数检验方法,用于评估两个分类变量之间的关联性或独立性。
使用条件:适用于n×m列联表,无序分类变量。
场景和临床应用:在医学研究中,卡方检验常用于评估疾病与风险因素、疗效与治疗方法等之间的关系。
连续性校正χ²(Continuity-corrected Chi-square)
定义:连续性校正卡方检验是卡方检验的一种修正方法,用于修正列联表中离散数据的近似误差。
使用条件:适当列联表大于2×2时,当总N值(在列联表中评估的总样本量)小于40时,需要使用Yates连续性校正来补偿理论概率分布(平滑)与实际观察值之间的偏差。
似然比(Likelihood ratio)
定义:似然比是一种比较两个模型拟合数据优度的方法,通常用于参数估计和假设检验。
使用条件:适用于n×m列联表。
场景和临床应用:在医学研究中,似然比检验用于评估诊断试验、疗效与治疗方法等之间的关系。
Fisher’s 精确检验(Fisher’s Exact Test)
定义:Fisher’s 精确检验是一种非参数检验方法,用于评估两个分类变量之间的关联性或独立性。
使用条件:适用于n×m列联表,特别是当超过20%的单元格期望频数小于5时,使用近似方法可能不准确,此时需要使用Fisher’s 精确检验。Fisher’s 精确检验通过应用列联表中各单元格数值的超几何分布来评估独立性的原假设。
场景和临床应用:在医学研究中,Fisher’s 精确检验常用于评估稀有疾病与风险因素、疗效与治疗方法等之间的关系,尤其在样本量较小或期望频数不满足卡方检验条件的情况下。
Z检验(Z-test)
定义:Z检验是一种基于正态分布的参数检验方法,用于比较两个比例或比较一个比例与一个已知的参考值。
使用条件:适用于n×m列联表,适用于大样本数据,且样本分布近似正态分布。通常,当样本量较大且单元格中的期望频数足够大(大于5)时,Z检验的结果与卡方检验的结果相似。
场景和临床应用:在医学研究中,Z检验常用于评估疗效与治疗方法、疾病与风险因素等之间的关系,尤其在样本量较大且数据分布近似正态的情况下。
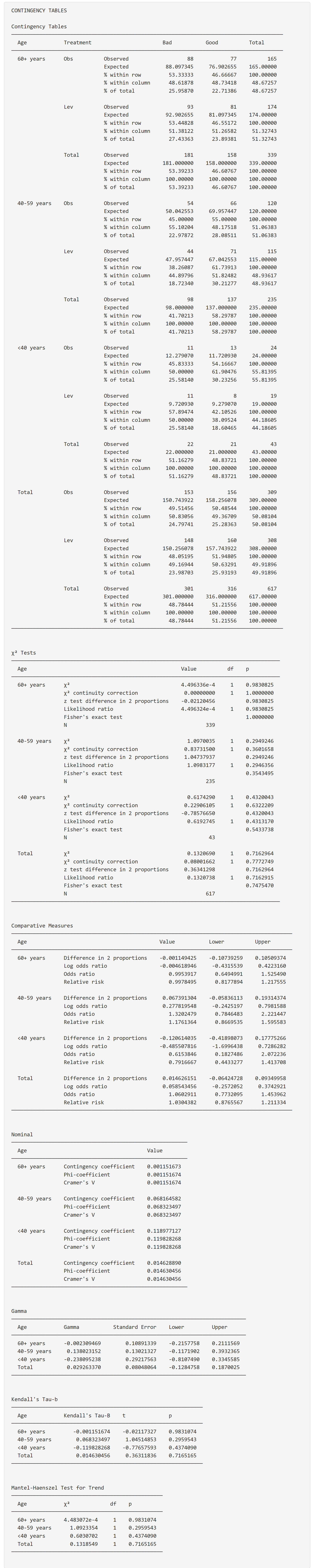
结果如下:

假设检验类型:
- 双侧检验(Two-tailed test)
定义:双侧检验是一种假设检验方法,用于评估观察差异的显著性,不论差异的方向。在双侧检验中,我们同时考虑了两个方向的极端值。
使用场景:当研究者对差异的方向没有预期或假设,或者对差异的方向不感兴趣时,使用双侧检验。例如,研究者希望检验两种药物的疗效是否有显著差异,但并不关心哪一种药物疗效更好。
功能:双侧检验主要用于评估两组之间的差异是否显著。例如:组1 ≠ 组2。
- 单侧检验(One-tailed test)
定义:单侧检验是一种假设检验方法,用于评估观察差异的显著性,只关注差异的一个方向。在单侧检验中,我们仅考虑一个方向的极端值。
使用场景:当研究者对差异的方向有明确预期或假设时,使用单侧检验。例如,研究者希望检验某种药物是否比对照组更有效。
功能:单侧检验主要用于评估两组之间的差异是否显著且符合预期的方向。例如:组1 > 组2 或 组1 < 组2。
总之,选择单侧检验还是双侧检验取决于研究者的预期和假设。在实际研究中,如果对差异方向有明确预期,可以使用单侧检验;否则,使用双侧检验更为保守且可靠
9.4.5 测量值
可以勾选需要计算的测量值:
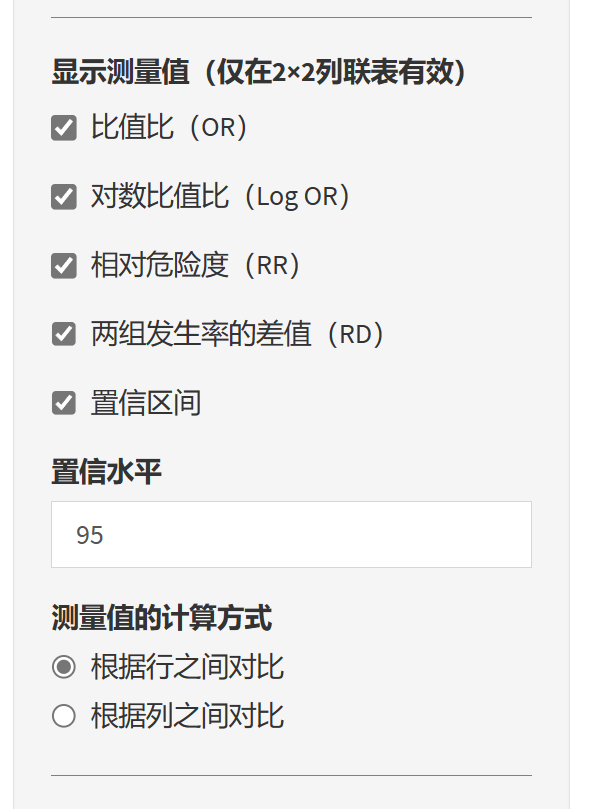
测量指标的介绍:
- 比值比(Odds Ratio, OR)
定义:比值比是一种用于量化两个事件A和B之间关联强度的统计量。比值比定义为在B存在时A的几率与在B不存在时A的几率之比,或等效地(由于对称性),在A存在时B的几率与在A不存在时B的几率之比。两个事件相互独立当且仅当比值比等于1,即一个事件在另一个事件存在或不存在时的几率相同。如果比值比大于1,则表示A和B之间存在关联(相关),相较于B不存在的情况下,B存在时A的几率增加,同样地,A存在时B的几率增加。相反,如果比值比小于1,则A和B之间呈负相关,一个事件的存在降低了另一个事件的几率。
功能:评估两组之间事件发生概率的相对差异。
使用案例:在研究吸烟与肺癌发病率的关系时,可以计算吸烟者与非吸烟者发生肺癌的比值比,以评估吸烟对肺癌发病率的影响。
- 对数比值比(Log Odds Ratio, Log OR)
定义:对数比值比是比值比的自然对数。将比值比取对数可以使其更接近正态分布,便于进行参数估计和检验。
功能:用于比较两组之间事件发生概率的相对差异,便于进行参数估计和检验。
使用案例:在分析药物疗效的临床试验中,可以计算实验组和对照组的对数比值比,以评估药物对治疗效果的影响。
- 相对危险度(Relative Risk, RR)
定义:相对危险度是一种用于比较两组之间事件发生的相对风险的指标。它表示一组中事件发生的概率与另一组中事件发生的概率之间的比值。
功能:评估两组之间事件发生风险的相对差异。
使用案例:在研究高血压患者与非高血压患者心脏病发病率的关系时,可以计算高血压患者与非高血压患者发生心脏病的相对危险度,以评估高血压对心脏病发病风险的影响。
- 两组发生率的差值(Risk Difference, RD)
定义:两组发生率的差值是一种用于比较两组之间事件发生的绝对差异的指标。它表示一组中事件发生的概率与另一组中事件发生的概率之间的差值。
功能:评估两组之间事件发生风险的绝对差异。
使用案例:在评估某种疫苗的有效性时,可以计算接种疫苗组和未接种疫苗组发生某种疾病的发生率差值,以评估疫苗的预防效果。
结果如下:
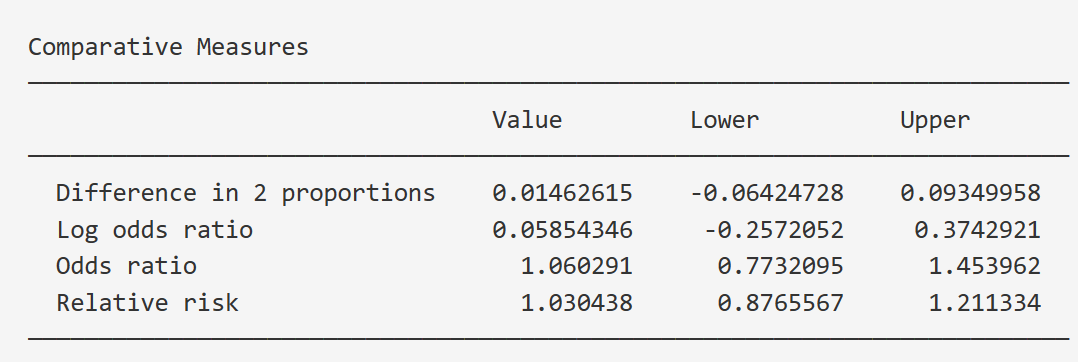
无序分类变量和有序分类变量的统计指标:

- 无序分类变量的统计
a. 列联系数(Contingency coefficient)
定义描述:列联系数是一种用于度量列联表中两个无序分类变量间关联强度的指标,其取值范围为0到1,值越接近1表示关联程度越高。
功能描述:评估两个无序分类变量间的关联程度。
使用场景案例描述:在研究患者的性别与某种疾病(如高血压)的关系时,可以使用列联系数来衡量性别与疾病之间的关联程度。
b. φ系数(Phi coefficient)和 Cramer’s V系数
定义描述:φ系数和 Cramer’s V系数都是衡量列联表中两个无序分类变量间关联强度的指标。φ系数适用于2×2列联表,而Cramer’s V系数适用于n×m列联表。它们的取值范围为0到1,值越接近1表示关联程度越高。
功能描述:评估两个无序分类变量间的关联程度。
使用场景案例描述:在研究某种疾病(如糖尿病)与患者的生活习惯(如饮食、运动)之间的关系时,可以使用Cramer’s V系数来衡量这两个无序分类变量之间的关联程度。
- 有序分类变量的统计
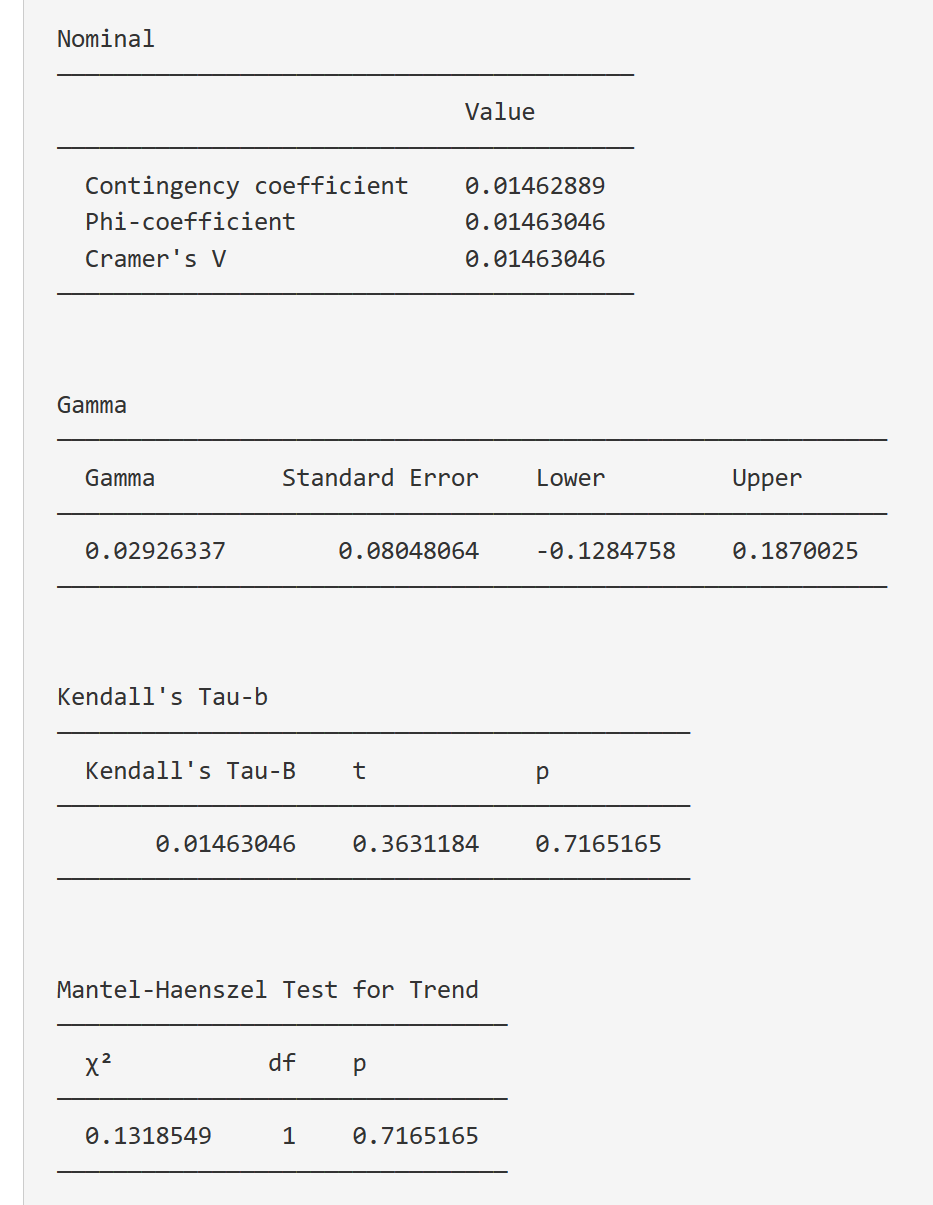
a. Gamma系数
定义描述:Gamma系数是一种用于度量两个有序分类变量间关联强度的指标,其取值范围为-1到1。正值表示正相关,负值表示负相关,绝对值越接近1表示关联程度越高。
功能描述:评估两个有序分类变量间的关联程度。
使用场景案例描述:在研究患者癌症分期与预后生存状态的关系时,可以使用Gamma系数来衡量这两个有序分类变量之间的关联程度。
b. Kendall’s Tau-b系数
定义描述:Kendall’s Tau-b系数是一种用于度量两个有序分类变量间关联强度的指标,其取值范围为-1到1。正值表示正相关,负值表示负相关,绝对值越接近1表示关联程度越高。
功能描述:评估两个有序分类变量间的关联程度。
使用场景案例描述:在研究疼痛评分与镇痛药物剂量之间的关系时,可以使用Kendall’s Tau-b系数来衡量这两个有序分类变量之间的关联程度。
c. Mantel-Haenszel趋势检验
定义描述:Mantel-Haenszel趋势检验是一种用于分析有序分类变量在分层数据中的关联趋势的统计方法。它可以帮助研究者评估有序分类变量之间的关联是否具有一致性。
功能描述:评估有序分类变量在分层数据中的关联趋势,以确定其关联一致性。
使用场景案例描述:在研究多个年龄层次的患者中,药物治疗有效性与疾病严重程度之间的关系时,可以使用Mantel-Haenszel趋势检验来评估在不同年龄层中,药物治疗有效性与疾病严重程度之间的关联趋势是否一致。
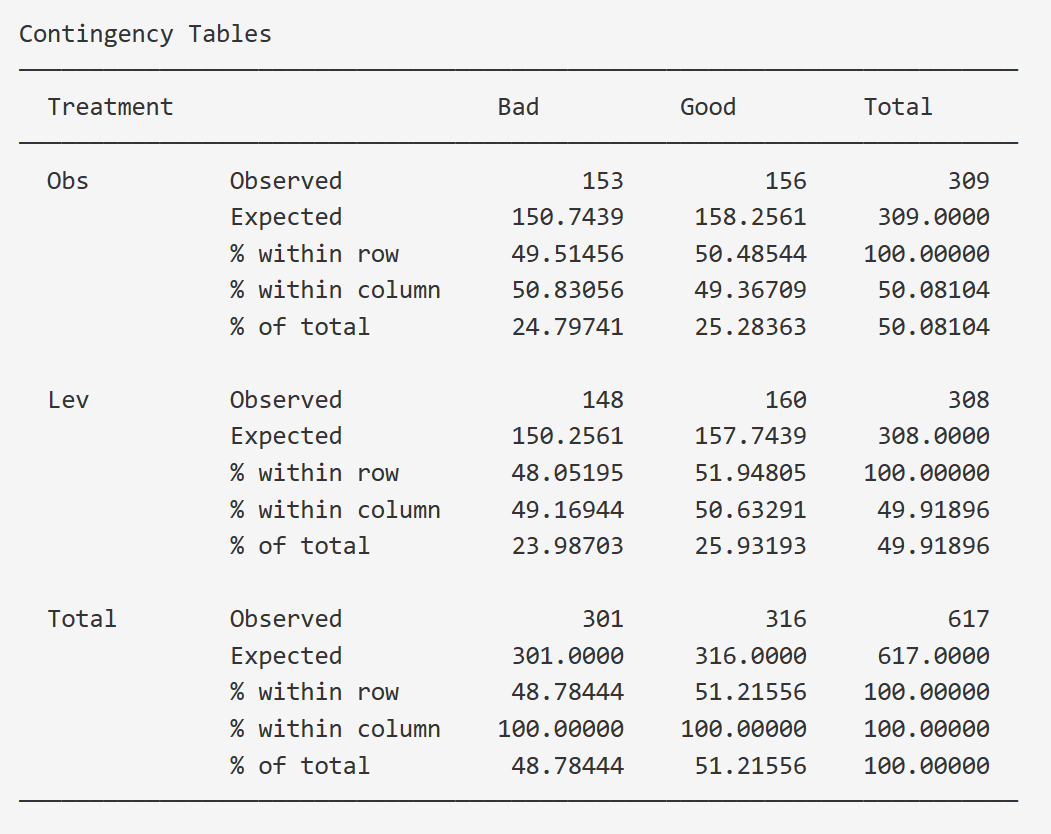
结果如下:
列联表的外观选项:

可以自定义需要展示的内容,结果如下:
9.5 配对样本 McNemar 检验
本节讲解如何在 本软件 中完成配对二分类数据的 McNemar 检验,并正确读取输出。应用场景:同一对象两次判定(如治疗前/后是否阳性)、成对匹配的病例–对照(1:1)等。不适用:两组互不重叠的独立个体(应做卡方/费舍尔),或类别数 > 2 的结局(需更换方法)。
9.5.1 背景与方法小百科
McNemar 检验是什么?
用于同一对象两次二分类判定(或匹配对)的一致性变化检验。只关注不一致的成对结果:
记 2×2 配对表为第二次=1 第二次=0 第一次=1 a b 第一次=0 c d 核心只看 b(1→0)与 c(0→1)。若 b 与 c 差距很大,说明“前后发生了系统性改变”。
统计量怎么来的?
经典近似:\(\chi^2 = \frac{(b-c)^2}{b+c}\)(自由度=1)。
连续性校正版更保守:\(\chi^2 = \frac{(|b-c|-1)^2}{b+c}\)。何时用“精确法(exact)”?
当 \(b+c\) 较小(经验上 < 25)时,建议使用精确二项(代码里显示为 exact log odds ratio 与精确 p 值),更稳妥。配对比值比(Paired OR)
McNemar 的“配对 OR”≈ \(b/c\)。若 1 在其区间外,则提示有方向性改变(例如“由阴变阳更多”)。
名词解释
二分类变量:仅两类,如“阳性/阴性”“是/否”。
配对/匹配:同一对象前后两次测量,或成对的两个对象(如病例与按性别/年龄匹配的对照)。
行/列变量:在 2×2 表中的“第一次判定”和“第二次判定”。
9.5.2 数据准备
支持两种数据形态,任选其一:
9.5.2.1 方式 A:个体级“宽表”(推荐,最直观)
- 每一行是一名受试者(或一对匹配个体),两列分别存第一次与第二次的判定结果(都必须是两个水平)。
- 类型在“定义字段”页设置为
factor,并确保恰好两类(如 0/1 或 阴/阳)。
示例(治疗前后是否阳性)
| id | pre (第一次) | post (第二次) |
|---|---|---|
| 1 | 阴 | 阴 |
| 2 | 阴 | 阳 |
| 3 | 阳 | 阴 |
| 4 | 阳 | 阳 |
| … | … | … |
准备要点 - 若显示为 numeric/character,请在 “定义字段” 改成 factor 并核对水平标签(建议先后顺序为“0/1”或“阴/阳”)。 - 只有两类;若出现第三种值(如“未测”),请先清洗或合并为缺失(NA)。
9.5.4 选择变量与参数
- 指定 2×2 变量
- “选择行变量(二分类变量)”:第一次判定(如 pre)。
- “选择列变量(二分类变量)”:第二次判定(如 post,不可与行变量相同)。
- “选择频数变量(可选)”:仅当采用“方式 B:汇总表”时勾选你的频数列(如 counts)。个体级宽表无需选择。
- “选择行变量(二分类变量)”:第一次判定(如 pre)。
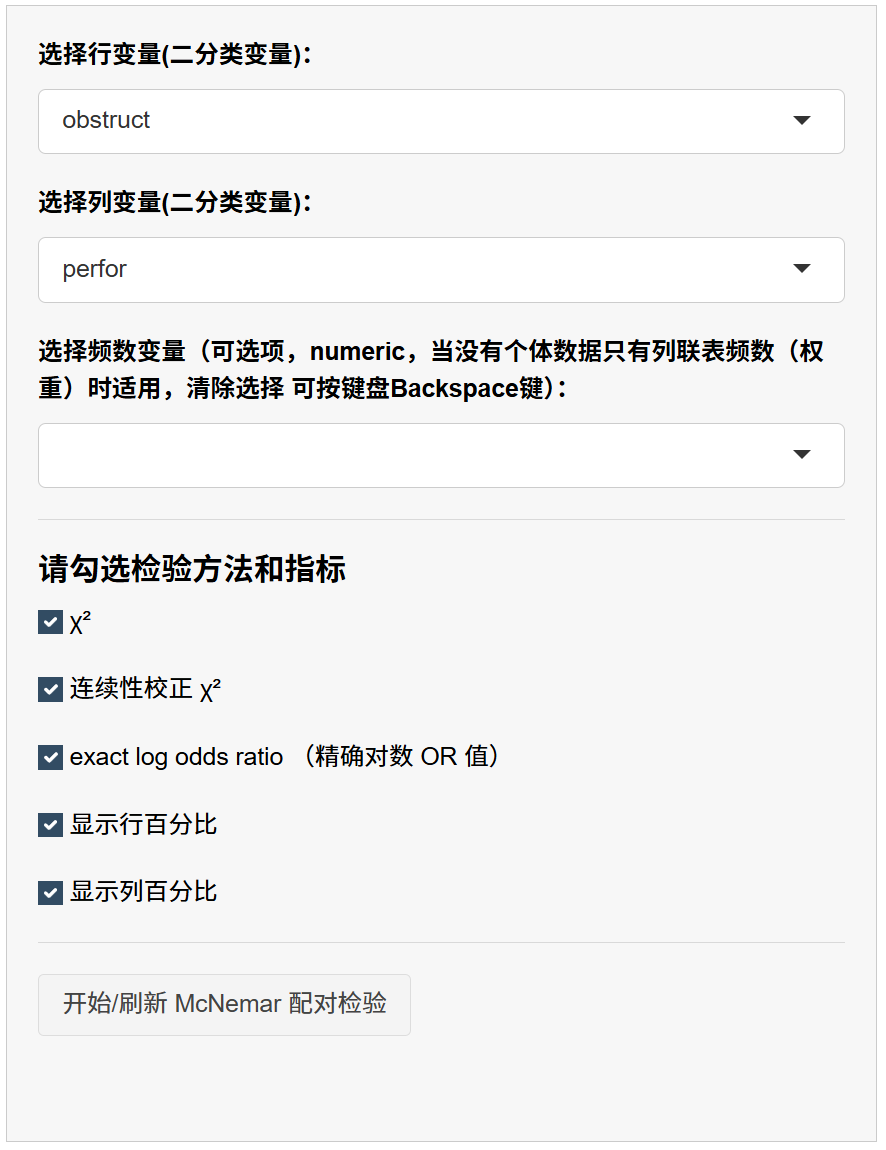
- 勾选检验与显示内容
- χ²:经典 McNemar \(\chi^2\) 近似检验。
- 连续性校正 χ²:更保守,样本不大时推荐一并查看。
- exact log odds ratio:给出精确法的配对 OR 与区间及 p 值(小样本更可信)。
- 显示行/列百分比:便于快速查看“由阴变阳/由阳变阴”的占比。
- χ²:经典 McNemar \(\chi^2\) 近似检验。
- 运行
点击 “开始/刷新 McNemar 配对检验”。
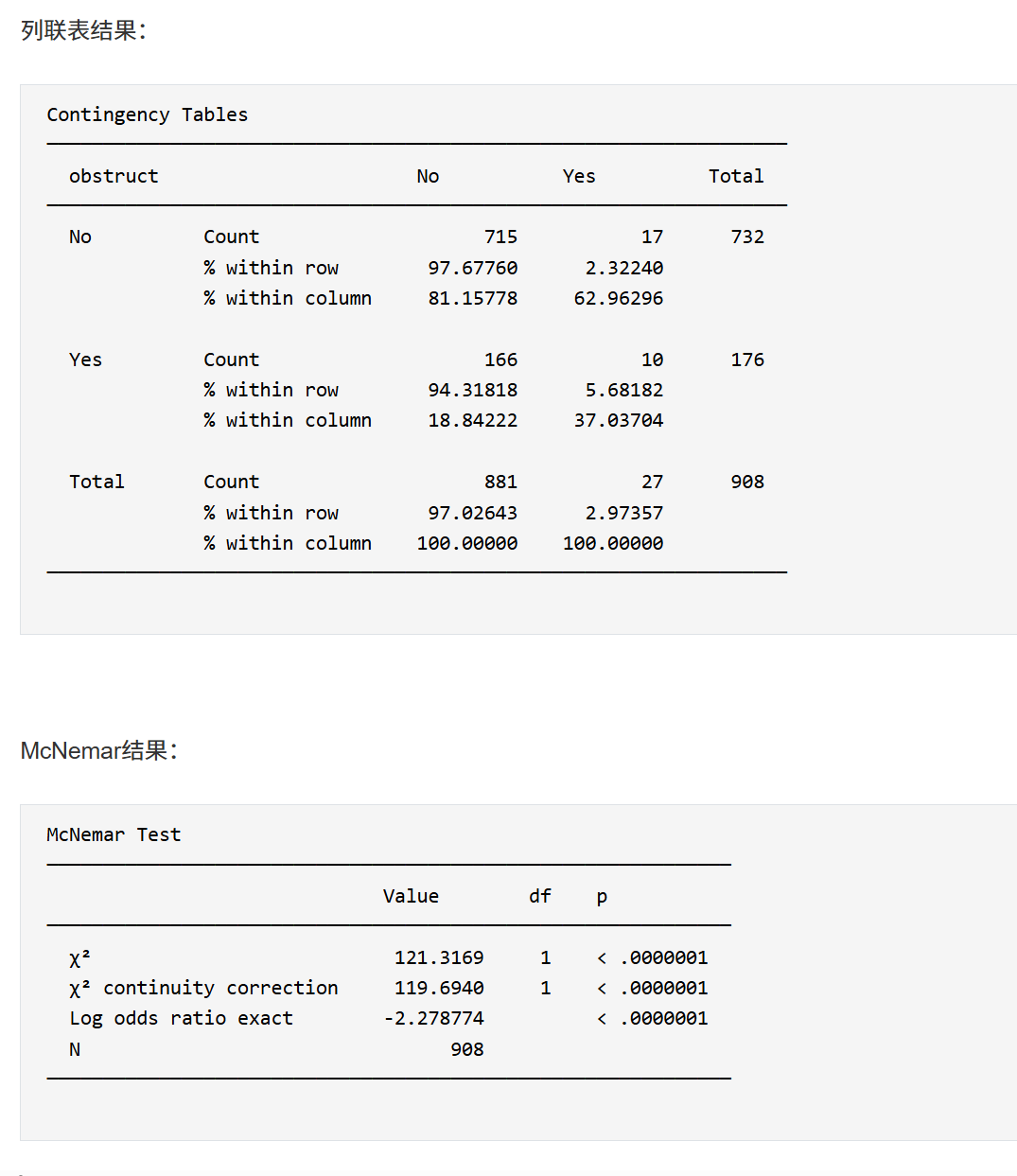
9.5.5 结果界面与读数指南
运行后依次显示两块文本输出:
- 列联表结果
- 展示 2×2 频数与(可选的)行/列百分比。
- 重点观察 b 与 c(不一致对),并记录 b+c 的大小(用于判断是否需偏重“精确法”)。
- 展示 2×2 频数与(可选的)行/列百分比。
- McNemar 结果
- 包含:χ²(是否带连续性校正)/ 精确法 的 统计量与 p 值,以及 log OR(≈ b/c)及其置信区间。
- 结论书写:若 p < 0.05(或小于你的显著性阈值),说明两次判定比例发生了显著改变;并注明改变方向(b>c 表示“1→0 多于 0→1”,反之亦然)。
- 包含:χ²(是否带连续性校正)/ 精确法 的 统计量与 p 值,以及 log OR(≈ b/c)及其置信区间。
选择哪一个 p 值?
- 样本较小或 \(b+c<25\):优先报告精确法。
- 样本较大:可报告连续性校正 χ²或标准 χ²,并与精确法核对是否一致。
9.5.6 结果解读范例(可改写)
- “对同一受试者的治疗前后阳性率进行 McNemar 检验:1→0 为 b=10,0→1 为 c=22,精确法 p=0.015,提示治疗后阳性率显著上升。配对 OR=2.20(95% CI 1.17–4.26)。”
- “病例–对照配对样本中,暴露前后差异采用 McNemar 进行检验,连续性校正 χ²=4.31,p=0.038,提示暴露改变与结局存在关联。”
9.5.7 常见问题与排查
- 行/列变量未出现:请在“定义字段”把它们设为
factor,且保证只有两类。
- 报错:levels 超过 2:请先在数据准备中合并为两类(如“阴/阳”),再导入或在“定义字段”中调整。
- 频数变量无法选择:仅当你采用“汇总表 + 频数列”的方式时才需要;否则留空。
- 精确法未输出/为 NA:检查 b+c 是否为 0(完全一致无变化时不可检验),或频数列是否为有效非负数值。
- 方向解释弄反:记得 log OR ≈ b/c;b>c 表示“从 1 变 0 更多”还是“从 0 变 1 更多”,取决于你对“1/0”的语义设定。
9.5.8 适用范围与不适用情形(容易混淆)
- 适用:
同一对象两次二分类判定(治疗前/后、检查法 A vs B)、1:1 匹配病例–对照的二分类结局比较。
- 不适用:
- 两个独立样本(用卡方/费舍尔);
- >2 类结局(需多分类配对方法);
- >2 次重复测量(考虑 Cochran’s Q 等)。
- 两个独立样本(用卡方/费舍尔);
9.6 对数线性回归
对于分类变量,常用卡方检验进行数据分析,但卡方检验更多的应用于二维列联表的情形,若列联表维度更高,如要同时研究多个分类变量间的关系,卡方检验显然不够,因为它不可能为多个分类变量间的关系给出一个系统而综合的评价,也不可能在控制其他因素作用的同时,对变量的效应作出估计。此时,除了用logistic回归模型分析之外,也可以考虑采用对数线性模型这一多元统计分析方法来研究多个分类变量之间的关系。
对数线性模型将列联表资料中各个格子理论频数的自然对数表示为各个分类变量的主效应,以及各个分类变量之间交互效应的线性模型。通过迭代计算估计模型中的参数,应用方差分析的思想,检验各分类变量的主效应和交互效应的大小。此时,不区分因变量和自变量,强调的是模型的拟合优度检验和分类变量间交互效应的检验。
以下是一个医学研究中应用对数线性回归的例子:
假设我们要研究某种疾病的发病与年龄段、性别和治疗方式之间的关系。在这个例子中,我们可以运用对数线性回归模型来分析这些分类变量之间的关联,从而为进一步的研究提供依据。
本软件 统计软件中的对数线性回归模块提供了对数线性回归的全面功能,包括:
设置因子:可根据研究目的设置一个或多个分类变量。
支持交互作用项:可以分析分类变量间的交互作用对关联的影响。
设置分类自变量的参照水平:方便进行多水平分类变量的比较。
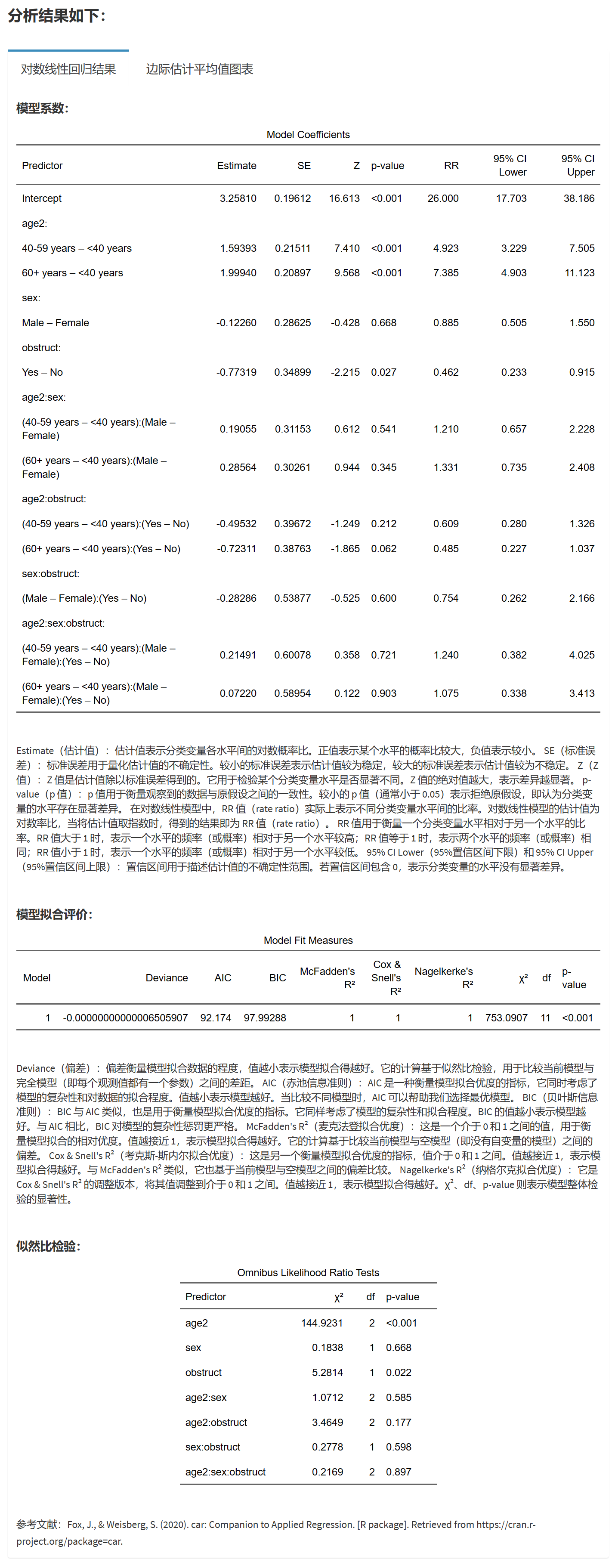
显示模型系数的置信区间、RR 值、RR 值的置信区间:方便对各分类变量的关联程度进行评估。
Omnibus 似然比检验:检验模型整体的显著性。
模型拟合优度评价:包括 Deviance、AIC、BIC、McFadden’s R²、Cox & Snell’s R²、Nagelkerke’s R²、χ²、df 和 p-value。
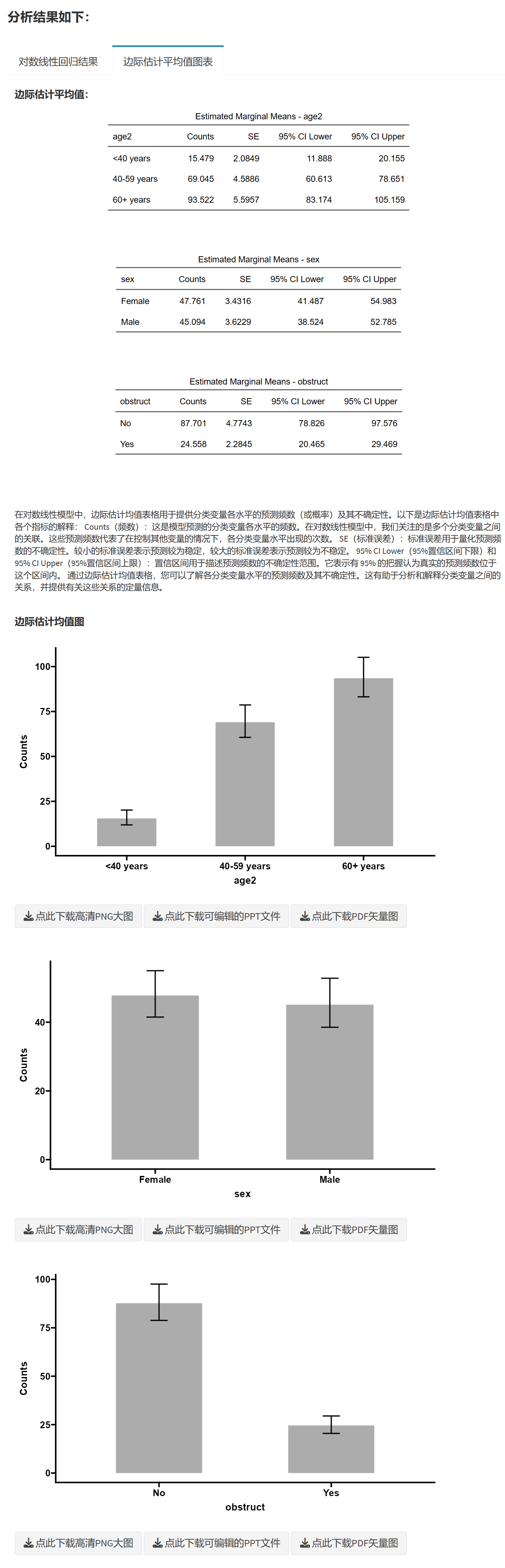
做估计边际平均值统计图表:包括生成预测频数及其不确定性的图表。
通过 本软件 对数线性回归模块,您可以轻松地进行多分类变量关联分析,并获得全面的统计结果。这有助于为您的研究提供定量信息,以及用于评估模型拟合优度和显著性的各种指标。

9.6.1 准备数据
可按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
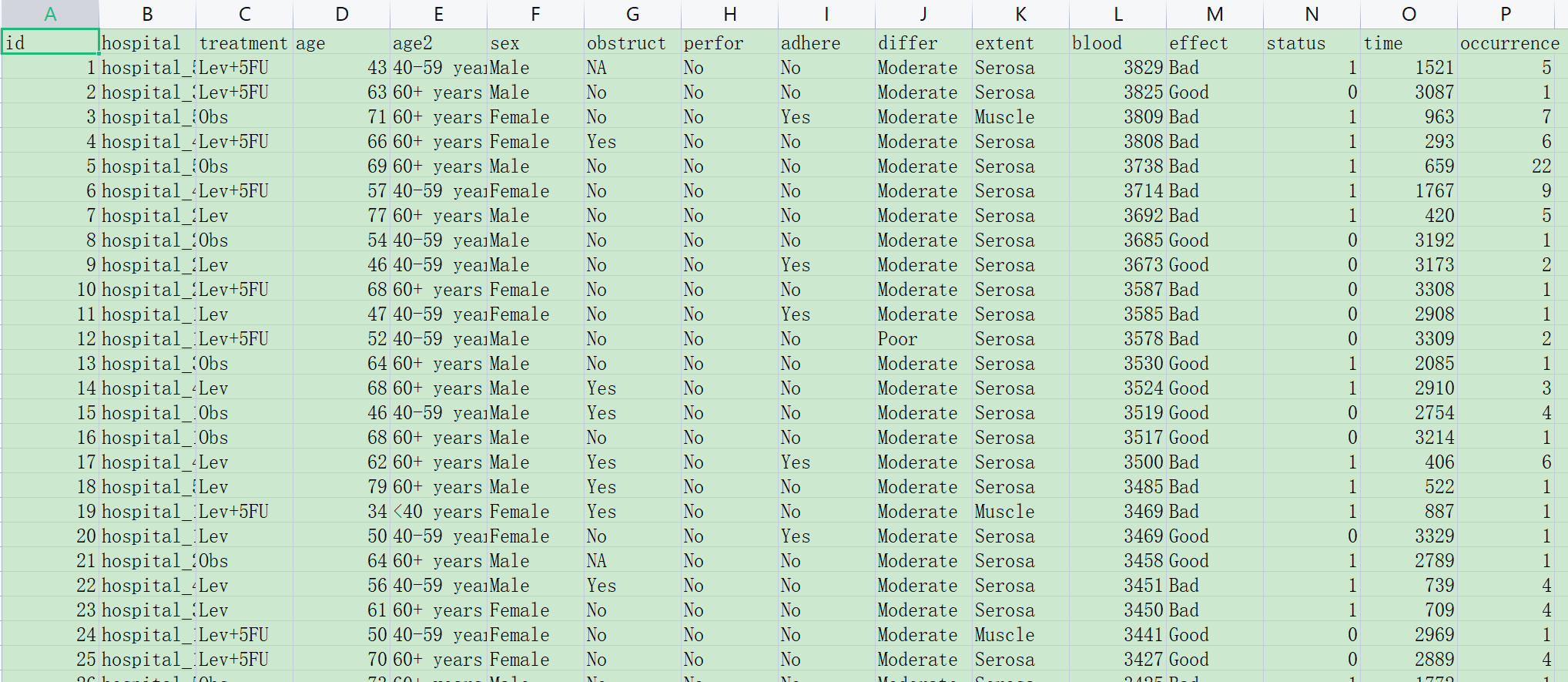
本样例数据的规则:
变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄(岁)、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 Age和Blood_test是连续性变量(numeric), 其他的是分类变量(factor)。
在对数线性回归中,只纳入分类变量,类似多维度的列联表概念。
9.6.2 对数线性回归分析
下一步就是对数线性回归分析啦:
使用方法和步骤如下:
在”请点击空白框选择因子,多选”框中选择多个因子,这些因子将用于对数线性回归分析。
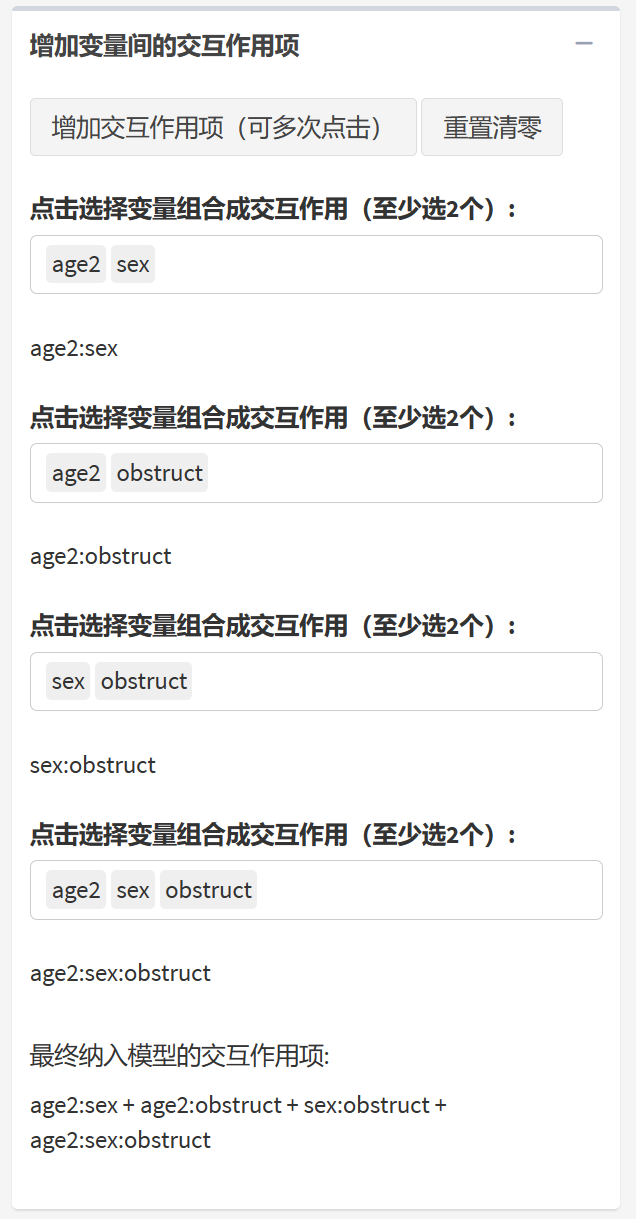
点击”增加交互作用项(可多次点击)“按钮,可以为模型添加交互项。可以多次点击以添加多个交互项。
点击”重置清零”按钮,清除已添加的交互项。
选择要作为参照组的非数值因子。
选择表示权重(频数)的变量(可选项)。
选择模型拟合优度评价的指标,如离差(deviance)、AIC、BIC、模型整体检验和伪R²(pseudo-R²)。
选择是否显示模型系数的置信区间,RR值和RR值的置信区间。
选择Omnibus检验的方法。
选择做边际平均值统计图表的方式,可以是对每个因素逐个单独做边际平均值统计图表,也可以是把多个因素交叉组合在同一个统计图表上展示边际平均值。
根据选择的边际平均值统计图表方式,选择因子或因子组合。
选择是否显示置信区间,如果显示,可修改置信水平。
调整统计图的宽度和高度。
最后点击”开始进行对数线性回归”按钮,程序将根据选择的设置进行对数线性回归分析。
在整个过程中,用户可以通过选择不同的因子、交互项和其他设置来自定义对数线性回归模型。分析完成后,将生成相应的统计结果和图表。
9.6.3 交互作用怎么选
对数线性模型的构建一般以饱和模型开始,饱和模型包含了所有变量的主效应,低阶交互效应和高阶交互效应。在本案例中,饱和模型包括以下部分:
age2、sex、obstruct 个主效应项;
age2:sex、age2:obstruct、sex:obstruct 3个二阶交互效应项;
age2:sex:obstruct 1个高阶交互效应项。
对数线性模型为层次模型,如果模型中包含了某几个变量的高阶交互效应项时,这几个变量的低阶交互效应项与主效应项也一定包含在模型中。但由于饱和模型的理论频数完全拟合了实际频数,因此在实际应用过程中的意义不大,所以需要找到最简约的模型,对变量之间的关系进行解释。拟合优度检验过程中通过后退法(即最先对饱和模型中的最高阶交互效应项进行假设检验,然后依次向次高阶和低阶交互效应进行假设检验)逐渐排除没有统计学意义的项,最后得到最优简化模型。
确定最优简化模型后,通常用最大似然估计法对拟合的简化模型参数进行估计。最大似然估计利用多项分布的原理构造自然函数,再求对数似然函数。由对数线性模型的结构可以发现,该模型不仅可以解决两个因素是否相关的问题。还可以用来分析各因素主效应是否起作用。如在本案例中,如果要想知道”age2”是否对”obstruct”起作用,则需要看”age2*obstruct”交互项是否有统计学意义。
9.7 单样本检验(单组率的描述和比较,二分类结局)
本节演示如何在 本软件 中完成单样本率(单组、二分类结局)的描述与假设检验:给定一个“理论/历史/目标比例”(检验值),比较本组观测到的发生比例是否等于该值;并批量生成整洁表格与 Word 报告。
9.7.1 背景与方法小百科(必读,面向零基础)
- 单样本率(one-sample proportion)
只有一组受试者、结局是两类(例如“有/无”“成功/失败”)。我们关心这组里“事件”(例如“有、成功”那一类)的比例是多少。
医学例子:某新方案客观缓解率(ORR)是否达到历史阈值 30%;术后并发症发生率是否低于院内红线 10%。 - 原假设(H0)与备择假设(H1)
给定“检验值” p0(如 0.3),检验观测比例 p̂ 是否与 p0 不同(双侧)、大于 p0、或小于 p0(单侧)。 - p 值
若 H0 为真,得到当前或更极端结果的概率。p 很小(如 <0.05)→“有统计学差异”。
温馨提醒:p 值不等于“差异大小”,也不等于“临床意义”。 - 置信区间(CI)
例如 95% CI 表示:若重复做很多次相同研究,95% 的这类区间会覆盖真实比例。
阅读技巧:95% CI 不跨过检验值 p0,与双侧检验显著性一致。 - 双侧 vs 单侧
- 双侧:只要“不等于”就算差异(默认,最稳妥)。
- 单侧:仅在事先明确且有理论依据的方向假设时使用(如“新方案不可能更差,只可能更好”)。
- 双侧:只要“不等于”就算差异(默认,最稳妥)。
- 小样本与稀有事件
小样本或比例靠近 0/1 时,区间会更宽;解读要结合临床意义与样本量(功效)考虑。
9.7.2 数据准备
数据为“宽表”:每行一个个体,每个待检的二分类变量一列(可一次选择多列,批量出结果)。
9.7.4 选择变量(可批量)
- 在 “选择因变量(二分类,也可多选进行批量分析)” 中勾选一个或多个二分类变量。
- 支持拖拽调整顺序。
- 若未出现在列表:回到 “定义字段” 将其设为
factor或numeric(仅两类)。
- 支持拖拽调整顺序。
名词解释:二分类变量只有两个取值(如“是/否、阳性/阴性、0/1”)。
9.7.5 设定检验值与备择假设
- “输入检验值”:填入历史阈值或目标比例 p0(0–1 之间;例如 0.3)。
- “假设检验类型(备择假设)”:
- ≠ 检验值(双侧,默认):检验 p̂ 是否不同于 p0。
- > 检验值(单侧):检验 p̂ 是否大于 p0(如疗效率是否≥目标值)。
- < 检验值(单侧):检验 p̂ 是否小于 p0(如严重不良事件率是否≤上限线)。
- ≠ 检验值(双侧,默认):检验 p̂ 是否不同于 p0。
小贴士
- 方向性检验仅在事先设定且有充分依据时使用;否则优先选用双侧。
9.7.6 置信区间与 p 值格式
- 勾选 “显示均值差的置信区间”(这里对应比例的 CI),并设置 置信水平(默认 95%)。
- 通过 “P 值保留几位小数” 设置报表中 p 值的展示位数(期刊常用 3 位)。
9.7.7 一键运行与结果解读
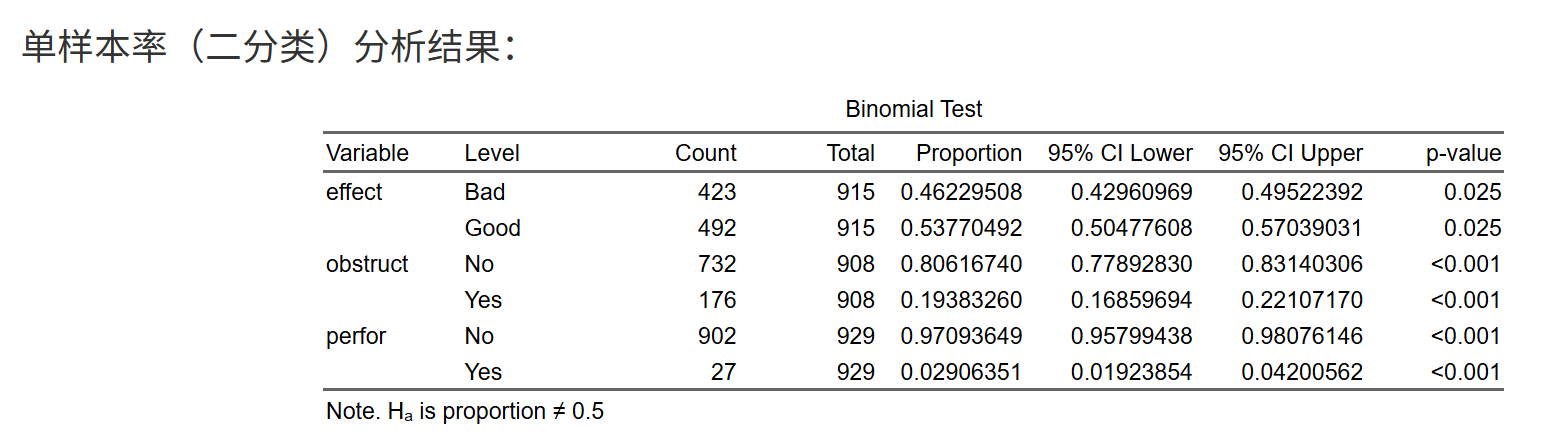
点击 “开始进行单样本二分类的检验分析”,将生成整洁表格,典型列含义:
- Variable / Level:变量名称及其两个水平(例如 Yes / No)。
- Count / Total / Proportion:该水平的例数、总例数、比例。
- 95% CI Lower / Upper(名称随置信度变化):比例的置信区间。
- p-value:单样本比例检验的 p 值。同一变量两行(两个水平)p 值相同,代表同一个检验;报告时只需引用你关心的“事件水平”一行即可。
读取示例:
“ORR=Yes 的比例为 42%(95% CI 30%–55%),与历史阈值 30% 比较,p=0.041(双侧)。”
9.7.9 缺失值处理与常见问题
- 缺失值:本模块按 jmv 默认行为对缺失进行处理。建议在导入前就完成缺失清理/合并,确保每列仅两类。
- 变量不是两类:请回到 “定义字段/数据准备” 合并水平或改造为严格二分类。
- p 值或区间异常:多见于样本量太小或比例极端(接近 0 或 1)。建议如实报告,并结合临床意义解读;必要时考虑扩大样本或更换研究设计。
- 关注哪一行?:通常报告“事件”那一行(例如 Yes);两行的 p 值相同,代表同一检验。
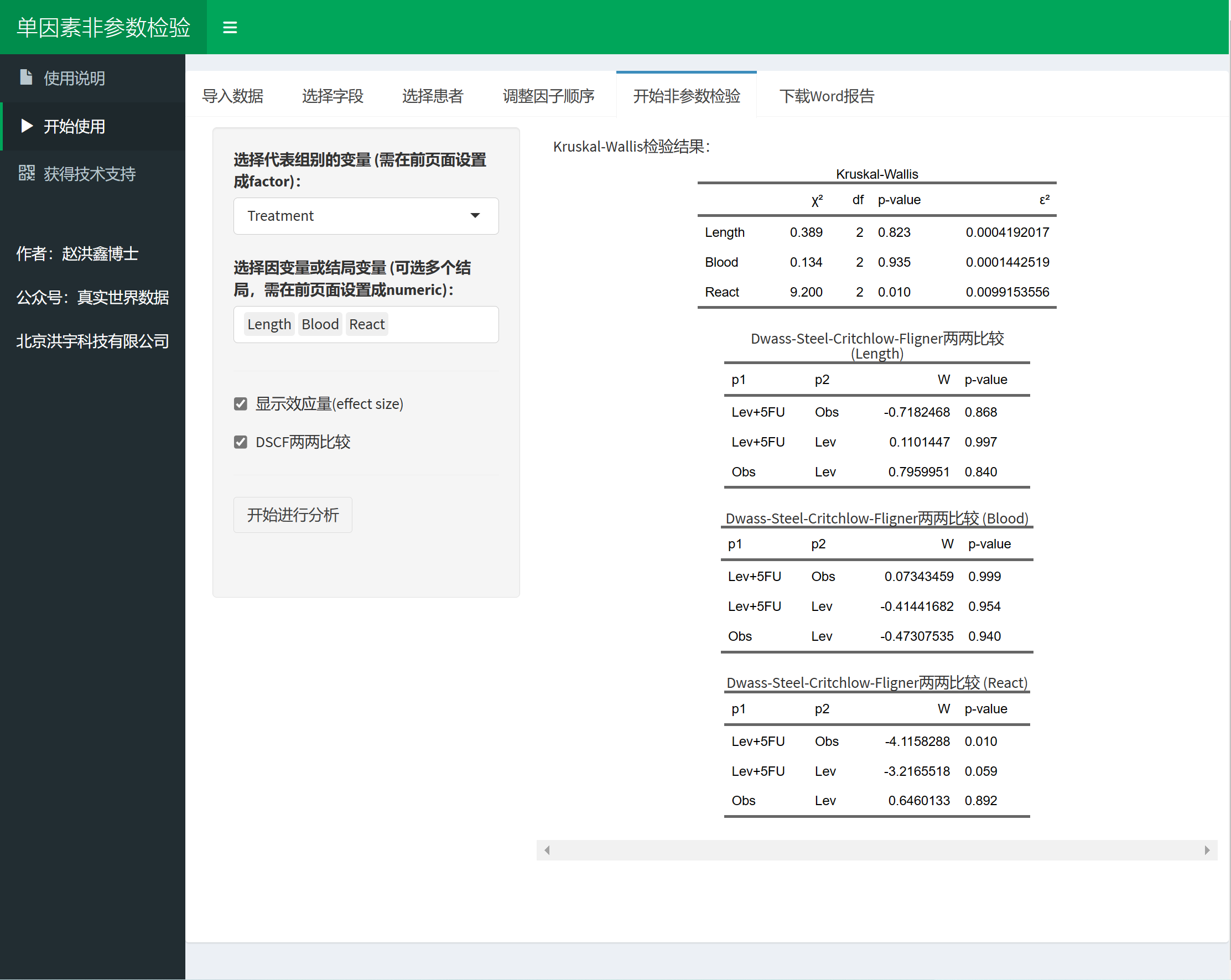
9.8 两组或多组非参检验(Kruskal-Wallis)
本统计模块 (Kruskal-Wallis检验) 适用于比较两组或两组以上分组时(如A、B、C治疗组),连续性变量(如某种检测,AST值,或其他临床结局)在不同分组的差异。当不满足正态分布及方差齐性时适用本模块。
- 整体Kruskal-Wallis检验
- 事后检验(两两比较):Dwass-Steel-Critchlow-Fligner 法
9.8.1 准备数据
到导入数据页面下载示例数据看一下:
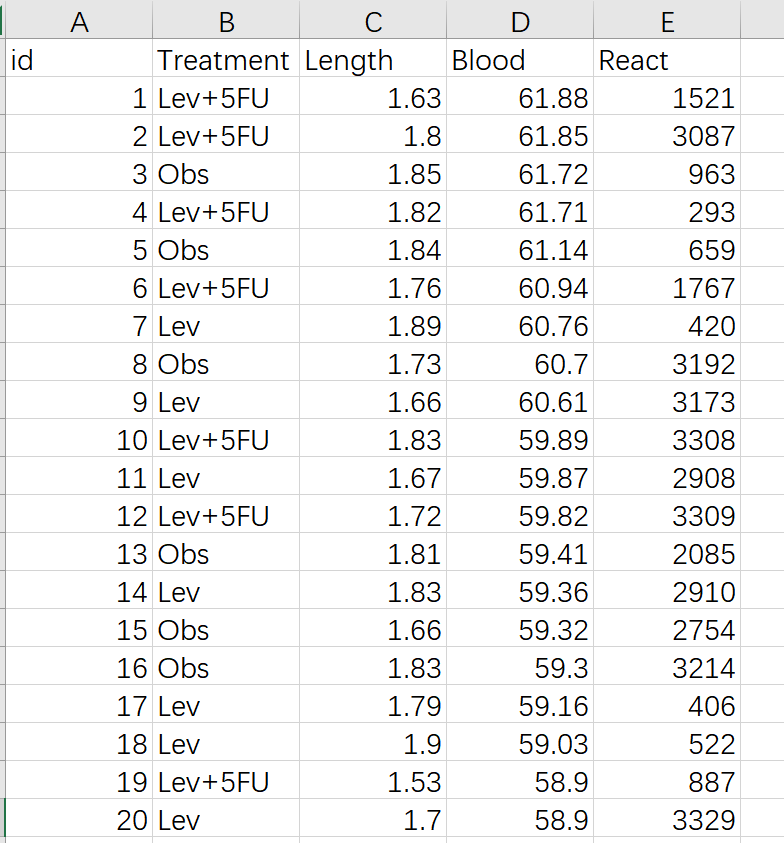
Treatment是代表治疗组别的变量,这里有三个组Lev, Obs, 和Lev+5FU组。需要把变量属性设置成factor
Length, Blood 和React是代表效果的变量,为连续性变量。需要把变量属性设置成numeric
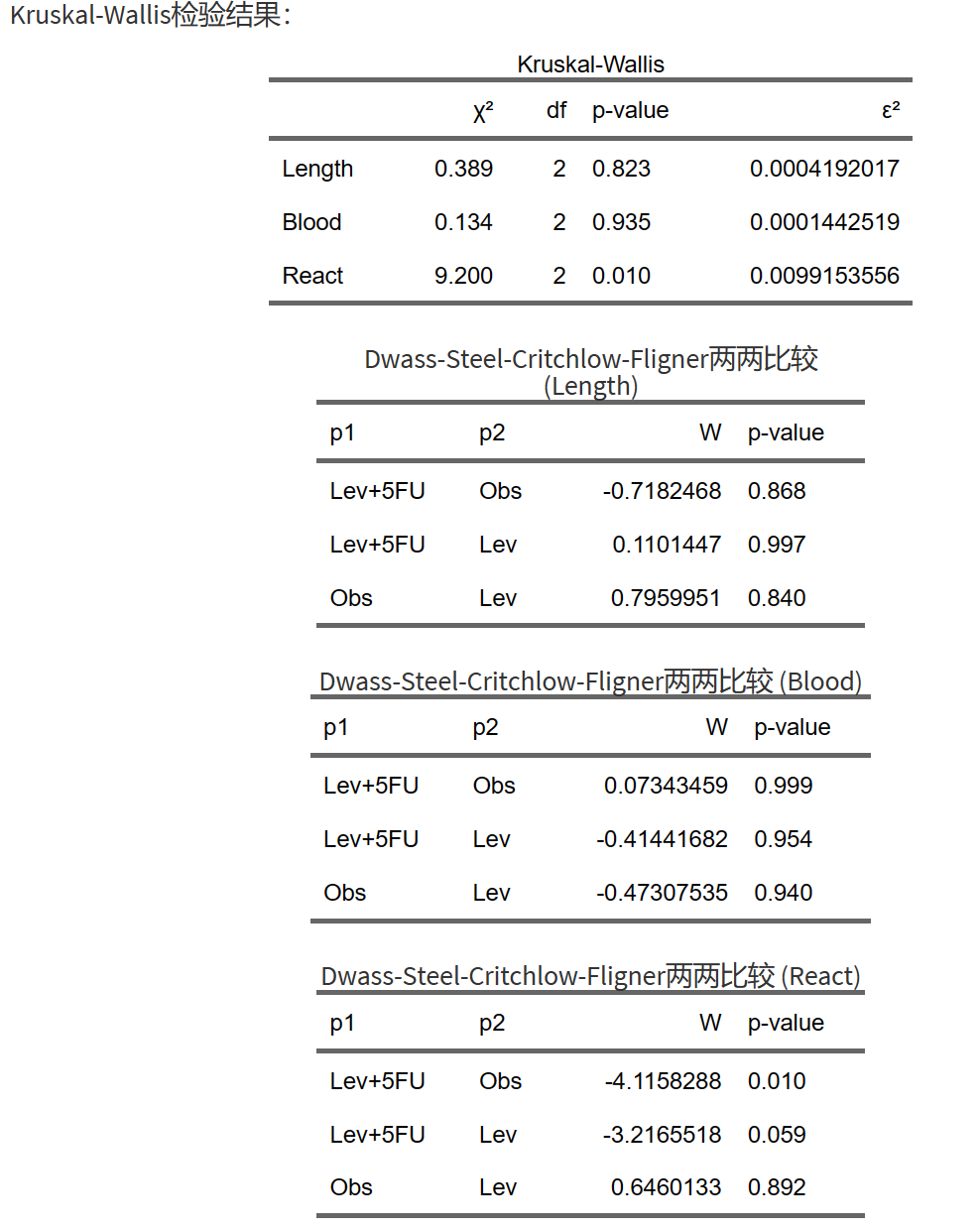
Kruskal-Wallis检验,主要看 三个组中,Length, Blood 或React 是否有差异。
另外可以进行事后分析,分别看上述指标在Lev vs. Obs, Lev vs. Lev+5FU, Obs vs. Lev+5FU对比中的差异。
9.9 配对或重复测量非参检验(Friedman)
Friedman 检验是一种非参数统计方法,用于分析配对资料和重复测量资料。这种方法主要用于研究时间或配对变量之间的差异,尤其适用于数据不满足正态分布或方差齐性假设的情况。
使用场景:
研究某种干预或处理在不同时间点的效果。
比较配对变量之间的差异。
例子1:临床上重复测量空腹血糖值,比较不同时间点血糖值的差异 在这个例子中,我们关注患者在不同时间点的空腹血糖水平。例如,我们可以在开始治疗前、治疗后1个月、治疗后3个月和治疗后6个月测量空腹血糖值。通过使用Friedman检验,我们可以检测不同时间点空腹血糖值之间的差异,以便了解患者的血糖控制情况。
例子2:比较不同训练方法对学生数学成绩的影响 在这个例子中,我们关注使用三种不同训练方法(如教材、在线课程和辅导)的学生在数学成绩上的表现。通过使用Friedman检验,我们可以检测三种训练方法对学生数学成绩的差异。这有助于我们了解哪种训练方法对学生数学成绩的提高效果最好。
本软件 医学科研统计机器人提供了一站式的Friedman检验步骤:
进行Friedman检验;
对各水平亚组进行两两比较(Durbin-Conover法);
描述性统计表和统计图:对数据进行描述性分析和绘制描述性统计图。
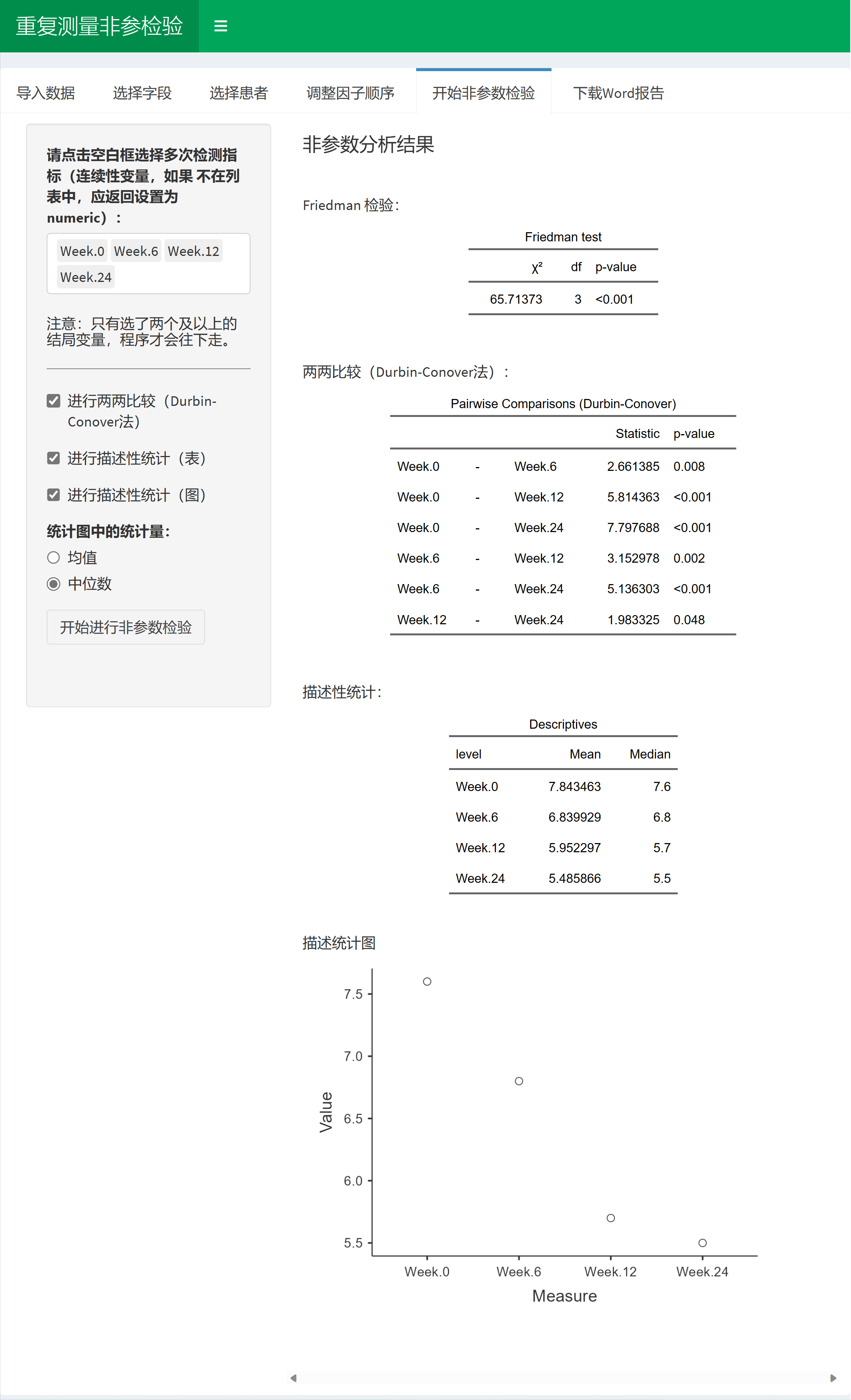
9.9.1 准备数据
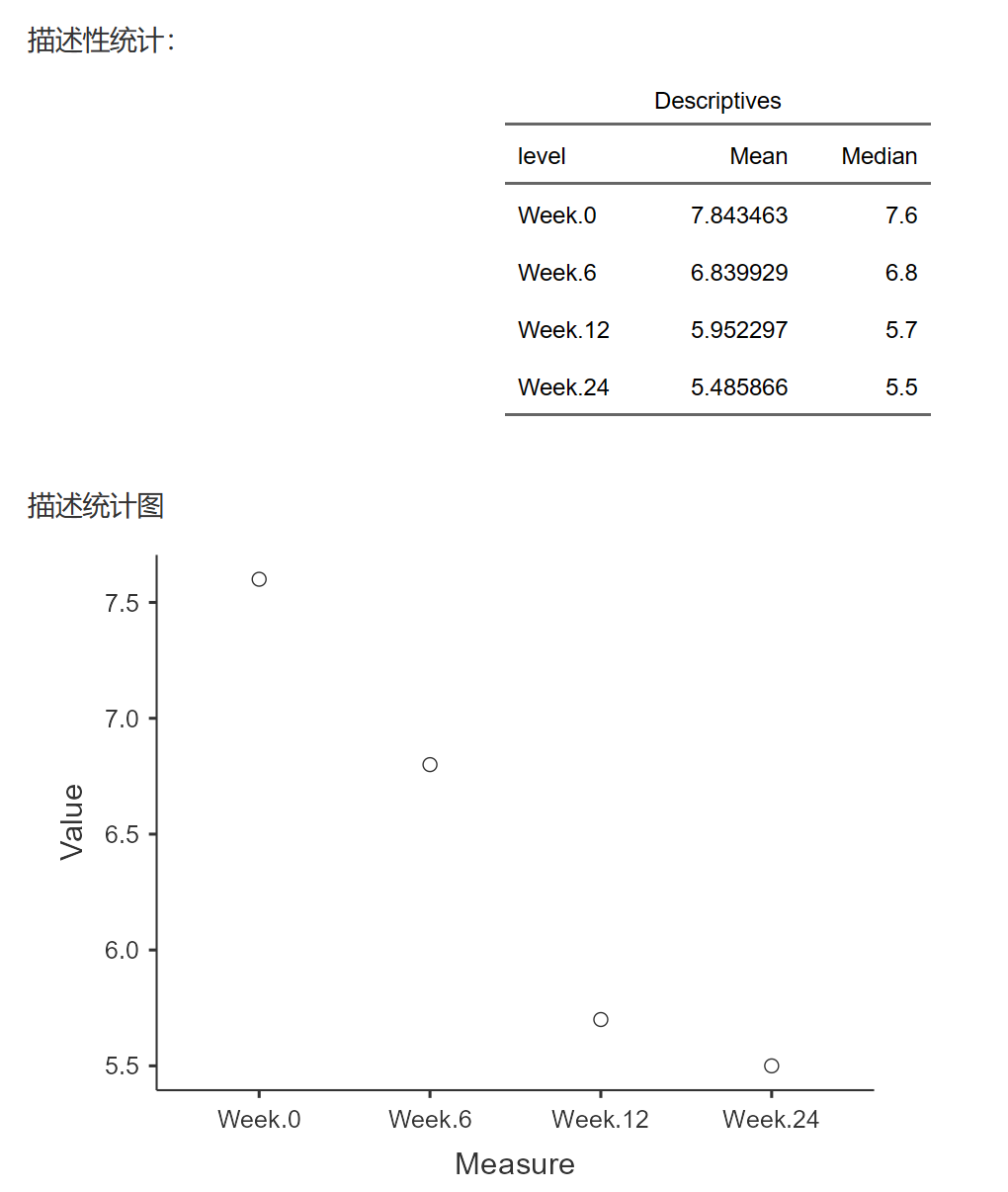
示例数据如下:
可按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
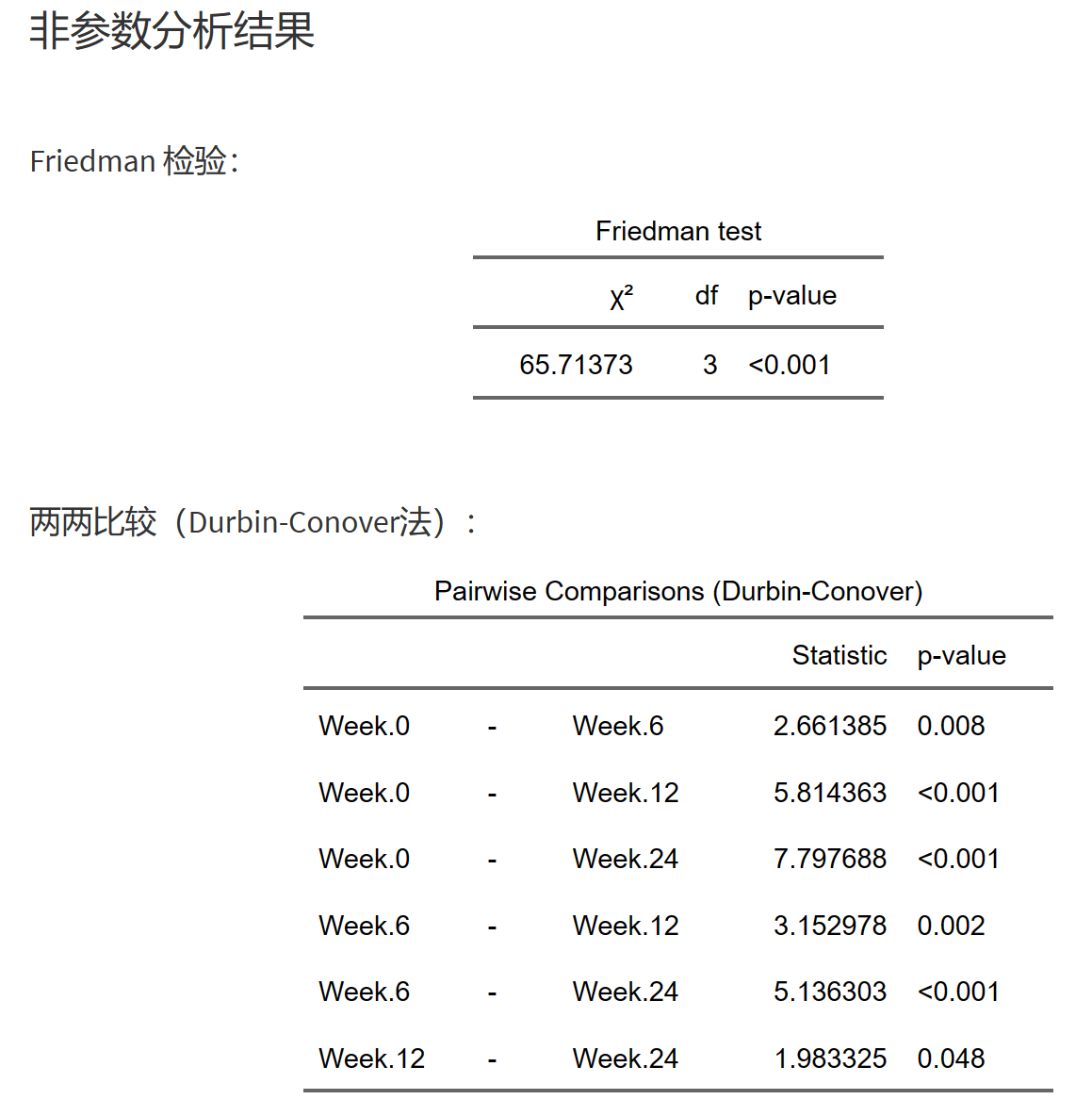
Week.0, Week.6, Week.12, Week.24 是一组重复测量的数据,为基线、6周、12周、24周的血糖值。
9.10 两个变量相关分析(Correlation)(基础版)
本节演示如何在 本软件 中完成两个连续变量的相关分析,支持 Pearson / Spearman / Kendall 三种相关系数,输出检验结果、置信区间与可复制的文字报告,并可一键导出 Word。适用于探索两个数值指标之间是否同向/反向随动,以及随动强度的大小。
典型医学场景:年龄与收缩压、CRP 与住院天数、肿瘤直径与手术时间等。
9.10.1 背景与方法小百科(必读)
- 相关系数:衡量两个变量“同涨同跌”的强弱,范围 -1 ~ +1。
- 0:几乎无线性关系;+1:完美正线性;-1:完美负线性。
- 常用解读(仅经验阈值):约 |r| 或 |ρ| = 0.1/0.3/0.5 → 弱/中/强。
- 0:几乎无线性关系;+1:完美正线性;-1:完美负线性。
- Pearson(皮尔逊):检验线性相关,对极端值敏感;前提近似为线性趋势 + 误差近似正态。
例:肌酐与尿素(通常近似线性)。 - Spearman(斯皮尔曼):对秩做相关,捕捉单调关系(不要求线性),抗极端值;偏态、等级数据、非线性单调时优先。
例:疼痛评分与镇痛用量(常单调但未必线性)。 - Kendall(肯德尔 τ):基于一致/不一致对的秩相关,样本量较小时更稳健,对并列值处理更友好。
例:样本量较小(如 n < 20)或大量并列秩。 - p 值与置信区间(CI):p 值检验“相关系数是否显著不为 0”;CI 提供估计不确定性(不跨 0 与双侧显著一致)。
- 重要提醒:相关 ≠ 因果。混杂因素、分层结构、非线性关系都可能导致“貌似相关”或“被稀释的相关”。
9.10.4 选择变量
- 第一个变量(X):在 “请选择第一个变量” 下拉框中选择(需为数值型)。
- 第二个变量(Y):在 “请选择第二个变量” 下拉框中选择(与 X 不同)。
若未在列表中出现,请回到 “定义字段” 将其属性设为
numeric后再返回。
9.10.5 设定检验选项
- 备择假设方式:
- 双侧检验(默认):只要相关 ≠ 0 就算显著。
- 单侧(大于/小于):仅在事先有明确方向性假设时使用。
- 双侧检验(默认):只要相关 ≠ 0 就算显著。
- 置信水平:默认 0.95(即 95% CI),可改为 0.90/0.99 等。
- 方法(method):
- Pearson:线性、近似正态、无明显极端值时。
- Spearman:偏态、单调非线性、受极端值影响时。
- Kendall:样本较小、大量并列秩或需更稳健时。
- Pearson:线性、近似正态、无明显极端值时。
9.10.6 运行分析
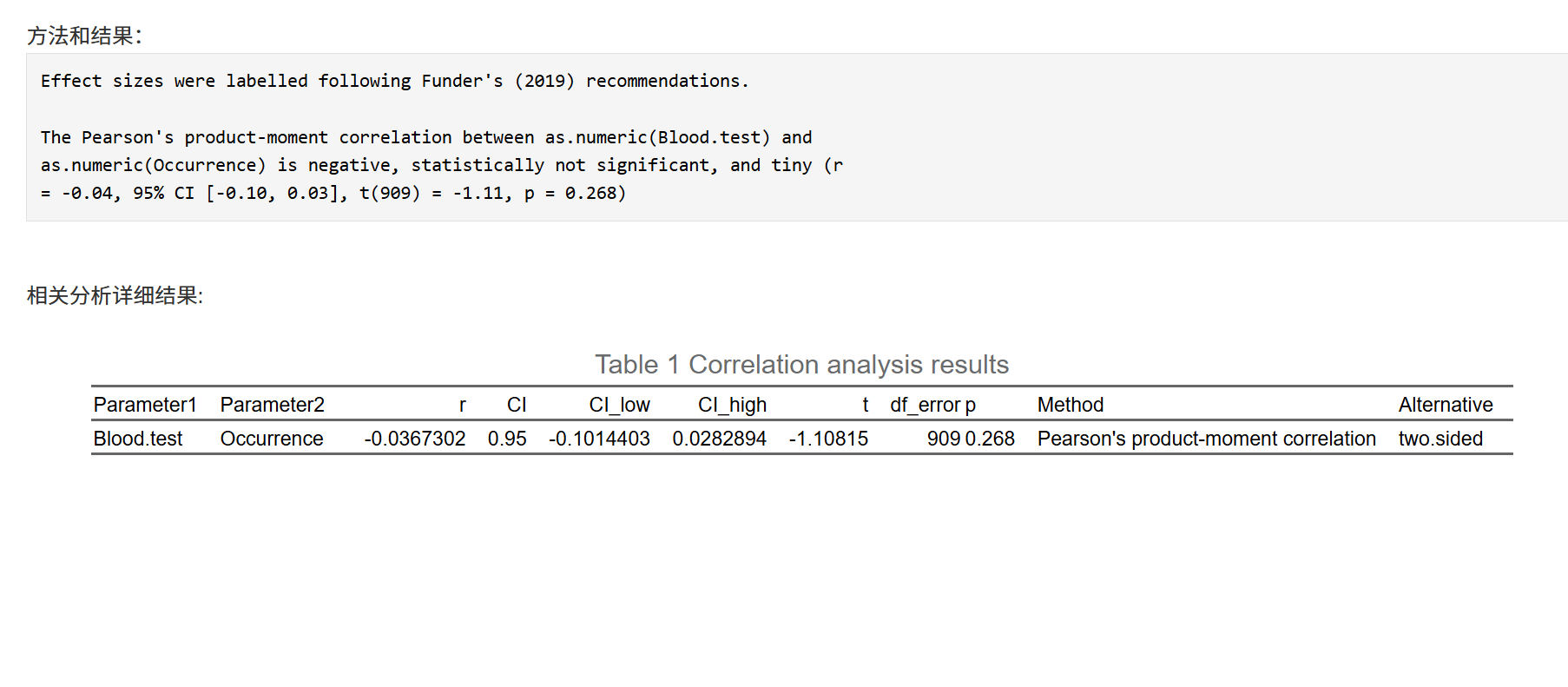
点击 “生成/更新…” 按钮后,右侧依次显示: 1) 方法和结果(文字报告):包含相关系数、p 值、置信区间与人类可读解读。
2) 相关分析详细结果(表格):便于复制到论文或补充材料。
9.10.7 结果解读(示例)
- “采用 Spearman 相关分析,Age 与 SBP 呈中等强度正相关:ρ = 0.42,95% CI [0.25, 0.56],p < 0.001。结果提示年龄越大,收缩压越高的单调趋势。”
- “采用 Pearson,r = 0.31(95% CI [0.12, 0.48],p = 0.002)。散点图显示大致线性,残差近似对称,无明显极端值。”
- “采用 Kendall,τ = 0.28(p = 0.004)。样本量较小并存在并列值,Kendall 结果更稳健。”
小贴士
- p 值反映“是否有统计学相关”,相关系数反映“相关有多强”。
- 置信区间跨 0 → 与双侧不显著一致。
- 若 Pearson 与 Spearman 方向一致但强度不同,优先依据更匹配前提的方法(偏态/极端值→Spearman/Kendall)。
9.10.8 导出 Word 报告
切换到 “下载Word报告” 页签,点击 “点此下载word文档”,将生成包含以下内容的文档: - 标题与Objective; - Method and Results 的可读性文字报告; - Correlation analysis results 表格(含系数、p 值与 CI)。
建议使用 Microsoft Word 打开(不要用 WPS,可能样式不兼容)。
9.10.9 常见问题与排查
- 变量不在下拉框:回到 “定义字段” 把变量类型设为
numeric;若是“数字形式的因子”,也建议改为数值。
- 结果受极端值影响:改用 Spearman/Kendall,并在报告中说明原因。
- 线性假设不满足:Spearman/Kendall 更合适;或考虑做非线性建模(如样条、局部回归),超出本模块范围。
- 混杂与分层:相关只是二元关系的表象;如疑似混杂(如年龄),请在后续回归模型中调整。
- 一眼看不出趋势:可能是“U 形/非单调”关系,相关系数可能接近 0;需画散点并考虑非线性方法(本基础版不含图形)。
- 缺失太多:系统会忽略成对缺失,若样本量骤降,请回到“数据准备”做缺失填补或核对数据质量。
9.10.10 适用与不适用情形
- 适用:两个连续指标之间的线性或单调关系探索与检验。
- 不适用:
- 一个或两个变量是分类变量(应考虑点双列/列联分析、回归等);
- 时间序列自相关、重复测量(需专业方法);
- 明显非单调关系(相关系数可能低估,需非线性方法)。
- 一个或两个变量是分类变量(应考虑点双列/列联分析、回归等);
9.10.11 报告写作模板(可直接改写)
- “采用 Pearson 相关分析,X 与 Y 呈 r = 0.36(95% CI [0.18, 0.51]),p = 0.0004 的正相关。考虑到散点图显示近似线性且无明显极端值,Pearson 的前提假设基本满足。”
- “由于 Y 分布偏态且存在极端值,使用 Spearman 相关分析:ρ = -0.29(95% CI [-0.45, -0.11]),p = 0.002。提示 X 越高,Y 越低的单调趋势。”
- “在样本量较小且并列值较多的场景下,采用 Kendall:τ = 0.22,p = 0.018,结论与 Spearman 一致,结果稳健。”
9.11 相关分析(Correlation)(高级版,支持 13 种相关)及相关系数矩阵
本节介绍如何在 本软件 的“相关分析(高级版)”模块中,完成多变量相关分析与相关系数矩阵的生成,支持 13 类常用/稳健/鲁棒相关方法,并导出 Word 报告与可下载的矩阵图。本文聚焦建模与出表,并补充一份相关方法百科(含参考文献),把用户当作统计学零基础来说明。
9.11.1 数据准备
数据形态:宽表(每列一个变量,每行一个受试者/样本)。
- 连续变量请在“定义字段”中设为
numeric/integer;
- 分类变量若用于有序/等级相关(如 Kendall、Gamma),可保留为
factor(有序因子更佳);
- 二分类变量(0/1、是/否、阳/阴)可用于 点二列/二列、四分相关(tetrachoric) 等。
变量与方法的匹配(快速对照)
| 方法(在模块中的名称) | 变量类型要求 | 场景示例 | 备注 |
|---|---|---|---|
| Pearson | 连续–连续 | 两项生化指标线性相关 | 对极端值敏感;线性关系假设 |
| Spearman | 等级/连续–等级/连续 | 疼痛等级与步行距离 | 单调关系即可,抗异常值 |
| Kendall | 等级–等级 | 症状分级与医生评分 | 对偏态更稳健,效率较高 |
| Biweight | 连续–连续 | 含少量离群值的实验测量 | 中位数为核心,抗离群 |
| Distance | 连续–连续 | 任意非线性关联 | 能抓住非线性/非单调 |
| Percentage bend | 连续–连续 | 噪声较多的测量数据 | 下调离群观测的权重 |
| Shepherd’s Pi | 等级/连续–等级/连续 | 先剔离群再做 Spearman | 鲁棒的秩相关 |
| Blomqvist | 连续/有序–连续/有序 | 总体中位数相依 | 以中位为核心的非参相关 |
| Hoeffding’s D | 连续/有序–连续/有序 | 任意依赖结构探测 | 可检出更广泛的依赖 |
| Gamma | 有序–有序 | 分级量表之间 | 对大量并列(ties)友好 |
| Gaussian rank | 连续/有序–连续/有序 | 鲁棒秩相关的替代 | 将秩映射到高斯分位 |
| Biserial(点二列/二列) | 连续–二分类 | 连续指标与阳/阴 | 用于一连续一二分类 |
| Tetrachoric | 二分类–二分类 | 两个二分类潜在连续 | 两侧都为二分类时使用 |
特别提醒
- 选择“自动选择(auto)”方法时:不能含缺失值(模块限制)。
- 相关分析会基于成对可用的观测进行计算(即某对变量有值才参与该对的计算)。
- 四分相关(tetrachoric)请确保两变量均为二分类且各格频数不为 0。
- Biserial适用于一连续 + 一二分类;若二分类是自然离散(不是潜在连续),“点二列/二列”解释更贴切。
9.11.4 设定备择假设与置信区间
- 备择(two.sided / greater / less):默认双侧,当你有明确方向性假设(且事先约定)时再选单侧。
- 置信水平(CI):默认 0.95(即 95% CI),可根据期刊要求调整。
9.11.5 选择相关方法(method)
- 在 “做相关分析的方法” 中选择(默认 Pearson)。
- 若数据含离群值/非线性/等级测量,考虑 Spearman/Kendall/Distance/鲁棒方法。
- 自动选择(auto):由程序为变量对自动匹配最合适方法(注意:入选变量需无缺失)。
9.11.6 多重比较校正(P 值)
- 在 “对 P 值进行多重比较调整的方法” 中选择:
- 常用:Holm(较 Bonferroni 稳健)、Bonferroni(保守)、BH/FDR(控制假阳性率)。
- 若变量较多,推荐 BH(FDR) 平衡发现与严格性;确认期刊要求后选择。
- 常用:Holm(较 Bonferroni 稳健)、Bonferroni(保守)、BH/FDR(控制假阳性率)。
9.11.7 一键运行与输出
点击 “生成/更新相关分析表”,主页面输出:
- 相关结果表(含相关系数 r/ρ/τ 或其他统计量、95% CI、P 值〔已按你的选择调整〕等);
- 切换到 “相关系数矩阵” 页,点 “生成/更新相关系数矩阵表/图”:
- 矩阵表:成对相关系数与(可选)显著性标识;
- 矩阵图:可视化相关强度与方向(色阶/大小)。图下方提供 PNG/PPT/PDF 下载按钮;可用滑杆调整图像宽高。
- 矩阵表:成对相关系数与(可选)显著性标识;
导出 Word:在 “下载 Word 报告” 页签导出,内含“相关结果表 + 相关矩阵 + 矩阵图”。
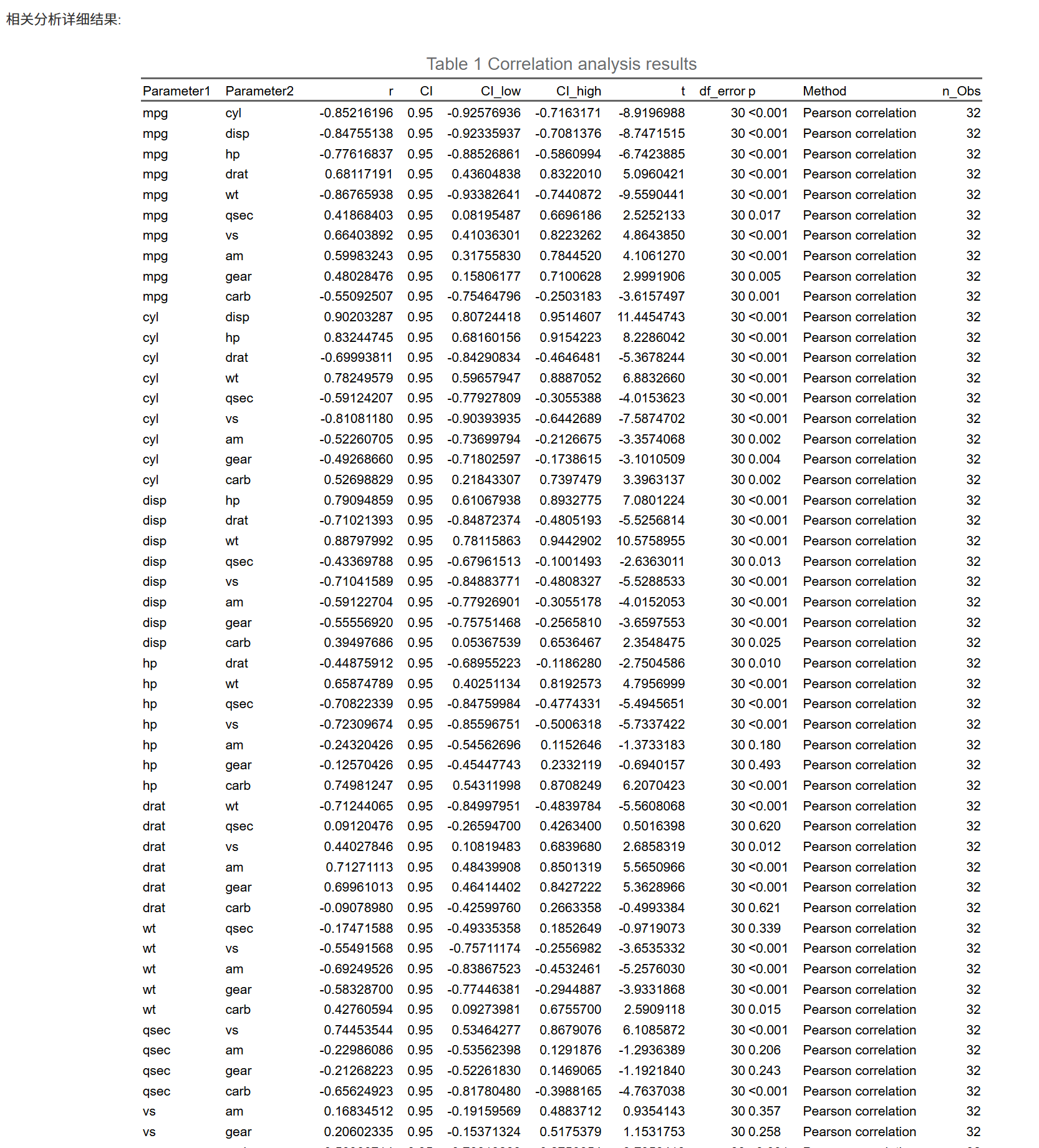
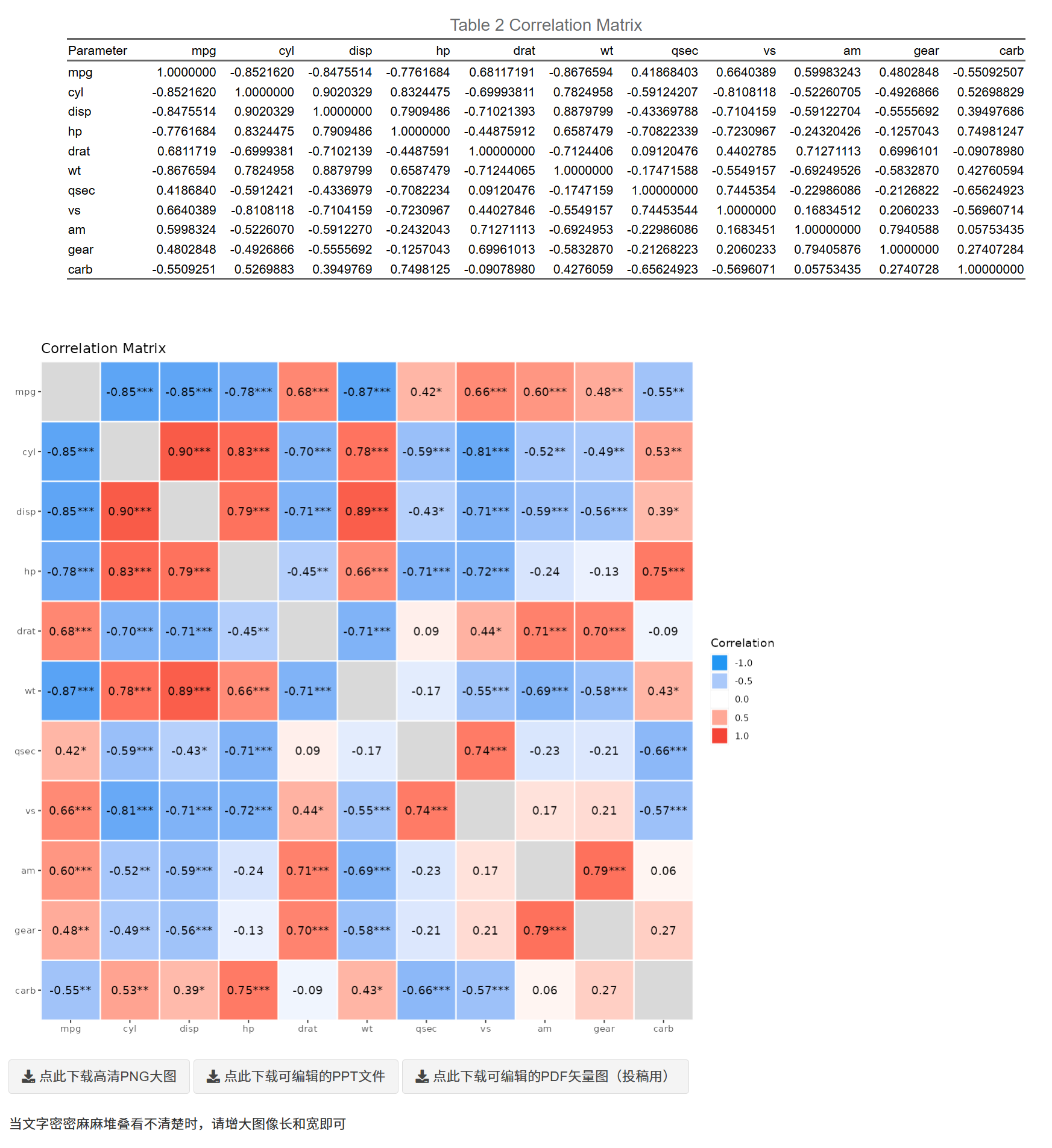
9.11.8 结果解读(给非统计背景的你)
系数大小(连续变量常见阈值,粗略):
| 绝对值 | 相关强度 | |—:|:—| | 0.1–0.3 | 弱 | | 0.3–0.5 | 中等 | | >0.5 | 较强 | > 注意:阈值仅作经验参考,应结合学科语境与样本量。显著性(P 值/CI):
- 95% CI 不跨 0 → 与双侧显著性一致。
- 多变量成对检验较多时请看校正后的 P 值或FDR。
- 95% CI 不跨 0 → 与双侧显著性一致。
方法选择的影响:
- Pearson反映线性关系;Spearman/Kendall反映单调/等级关系;Distance/Hoeffding可检出非线性依赖。
- 含离群值时,Biweight / Percentage bend / Shepherd’s Pi / Gaussian rank更稳健。
- 二分类场景用 Biserial(点二列/二列)/Tetrachoric 更贴切。
- Pearson反映线性关系;Spearman/Kendall反映单调/等级关系;Distance/Hoeffding可检出非线性依赖。
9.11.9 常见问题与排查
- 变量选不上/方法受限:检查“定义字段”的类型设置是否匹配方法要求。
- Auto 报错:入选变量不得含缺失;请先做缺失处理或改用手选方法。
- Tetrachoric 失败:检查两变量是否都是二分类,且四格频数均>0。
- 很多对都显著:请查看“多重比较校正”后的 P 值或 FDR;必要时收紧阈值。
- 图中文字重叠:在“相关系数矩阵”页调大图像宽度/高度。
9.11.10 报告撰写模板(可改写)
- “我们对 X 与 Y 进行相关分析。考虑到变量的等级/非正态特征,采用 Spearman 相关,结果 ρ = 0.34(95% CI 0.12–0.52),校正后 P = 0.004。作为敏感性分析,Distance 相关同向且显著。”
- “针对含离群值的数据,采用Biweight 作为鲁棒相关(r_bi = …);与常规 Pearson 方向一致。”
- “多变量成对比较共 m 对,对 P 值进行 BH-FDR 校正,以控制多重比较带来的假阳性。”
9.11.11 知识补给|相关类型详解(含参考文献)
下列解释帮助你理解每种相关系数的含义、适用场景与优缺点。括号内标注为本模块中的对应选项(如适用)。
Pearson’s correlation(皮尔逊,
pearson)
最常见的相关系数,度量两变量的线性关系;等于协方差除以两变量标准差的乘积。
适用于连续–连续且关系近似线性、无严重离群值的情形。Spearman’s rank correlation(斯皮尔曼,
spearman)
基于秩的非参数相关,等价于“将原值换成秩后再做 Pearson”。检验单调关系(不要求线性)。
Spearman 的 CI 可用 Fieller et al., 1957 的修正;见 Bishara & Hittner, 2017 的讨论。Kendall’s rank correlation(肯德尔,
kendall)
非参数秩相关,常较 Spearman 更稳健与高效(更小的总体误差敏感度与渐近方差)。
其 τ 的解释是“一致对与不一致对比例之差”。CI 同样可参考 Fieller et al., 1957。Biweight midcorrelation(
biweight)
基于中位数的相似性度量,对离群值不敏感,是 Pearson 的鲁棒替代(Langfelder & Horvath, 2012)。Distance correlation(
distance)
可检测线性与非线性的更一般的依赖关系,对复杂曲线型关系尤其有用。Percentage bend correlation(
percentage)
Wilcox (1994) 提出,对偏离中位数的边缘观测赋予较低权重(默认 20%),以降低离群影响。Shepherd’s Pi correlation(
shepherd)
先用自助法马氏距离识别/下调离群,再对秩做 Spearman,得到鲁棒秩相关。Blomqvist’s coefficient(
blomqvist)
又称 Blomqvist’s Beta / medial correlation(Blomqvist, 1950),基于中位的非参相关,
在含并列/非正态时相比 Spearman/Kendall 具有一定优势(见 Shmid & Schimdt, 2006 述评)。Hoeffding’s D(
hoeffding)
非参数秩统计量,能检测更一般的独立性偏离(包括非线性依赖;Hoeffding, 1948);取值范围约 [-0.5, 1](无并列时),值越大表示关系越强。Somers’ D(说明性,当前模块未实现)
非参数有序关联度量,常用于二分类结局与连续/有序预测之间(如逻辑回归情境)。本实现多用于二分类结局的有序关联度评估。Point-Biserial / Biserial(模块对应
biserial)
一连续 + 一二分类的相关系数。点二列等价于 Pearson;二列适用于“二分类来自潜在连续”的设定(如“焦虑程度”二分自连续)。模块提供biserial以覆盖这类情形。Gamma correlation(
gamma)
Goodman–Kruskal Gamma,与 Kendall’s Tau 类似,对大量并列情况表现更好,且相对稳健。Winsorized correlation(说明性,当前模块未实现)
对变量先做温莎化(阈值外的极端值被截断/替换)再计算相关,常用于减少可疑极端值的影响。Gaussian Rank correlation(
gaussian)
将秩映射到高斯分位后计算的相关,作为鲁棒秩相关的简单且性能良好替代(Boudt et al., 2012)。
见 Bhushan et al., 2019 在心理学网络中的应用。Polychoric correlation(说明性,当前模块未实现)
两个潜在正态的连续潜变量之间的相关,从两个观察到的有序变量估计而来。Tetrachoric correlation(
tetrachoric)
Polychoric 的特殊情形:两侧观测变量均为二分类。常用于潜在连续阈值模型下的二分数据。
如何选?超简化指南
- 线性且无显著离群:Pearson;
- 等级/单调、或对离群更稳健:Spearman / Kendall;
- 非线性/复杂依赖:Distance / Hoeffding;
- 离群明显:Biweight / Percentage bend / Shepherd’s Pi / Gaussian rank;
- 连续 vs 二分类:Biserial(点二列/二列);
- 二分类 vs 二分类(潜在连续):Tetrachoric。
9.11.12 参考文献
- Boudt, K., Cornelissen, J., & Croux, C. (2012). The Gaussian rank correlation estimator: robustness properties. Statistics and Computing, 22(2), 471–483.
- Bhushan, N., Mohnert, F., Sloot, D., Jans, L., Albers, C., & Steg, L. (2019). Using a Gaussian graphical model to explore relationships between items and variables in environmental psychology research. Frontiers in Psychology, 10, 1050.
- Bishara, A. J., & Hittner, J. B. (2017). Confidence intervals for correlations when data are not normal. Behavior Research Methods, 49(1), 294–309.
- Fieller, E. C., Hartley, H. O., & Pearson, E. S. (1957). Tests for rank correlation coefficients. I. Biometrika, 44(3/4), 470–481.
- Langfelder, P., & Horvath, S. (2012). Fast R functions for robust correlations and hierarchical clustering. Journal of Statistical Software, 46(11).
- Blomqvist, N. (1950). On a measure of dependence between two random variables. Annals of Mathematical Statistics, 21, 593–600.
- Somers, R. H. (1962). A new asymmetric measure of association for ordinal variables. American Sociological Review, 27(6).
以上文献为方法背景阅读。实际发表请按你的研究领域与期刊要求引用最贴切的来源与软件版本信息。
9.12 单因素方差分析(One-way ANOVA)
单因素方差分析是一种用于比较两个或多个组之间差异的统计方法。这种方法被用于确定一个或多个因素对于一个或多个连续型变量的影响,因素通常是指某一类别或者某个处理。在单因素方差分析中,一个连续型变量(称为因变量)在一个分类变量(称为自变量)的每一种水平(或组别)上被测量。
单因素方差分析,需要满足6个条件:
条件1:观察变量为连续变量。
条件2:观测值相互独立。
条件3:观测值可分为多组(≥2)。
条件4:观察变量不存在显著的异常值。
条件5:残差为正态(或近似正态)分布。
条件6:多组观测值的整体方差相等。
单因素方差分析常用于比较不同治疗方法对疾病的疗效。
本软件 医学科研统计机器人提供了一站式的单因素方差分析步骤:
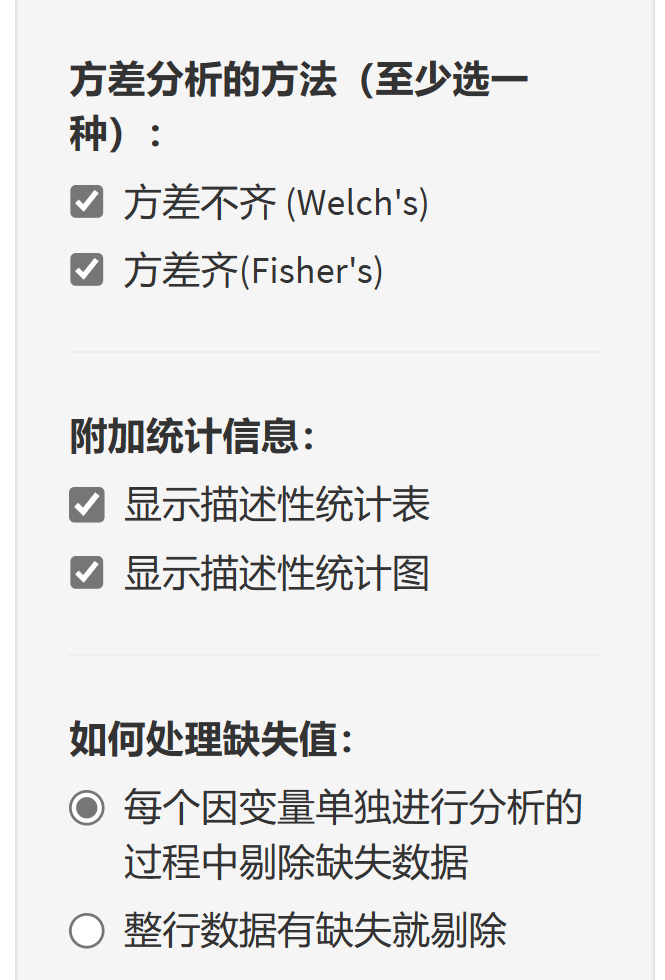
- 数据是否适合做方差分析:提供正态性检验、QQ图、方差齐性检验;
- 描述性统计:各组结局的均值、SE、95% CI 进行描述统计
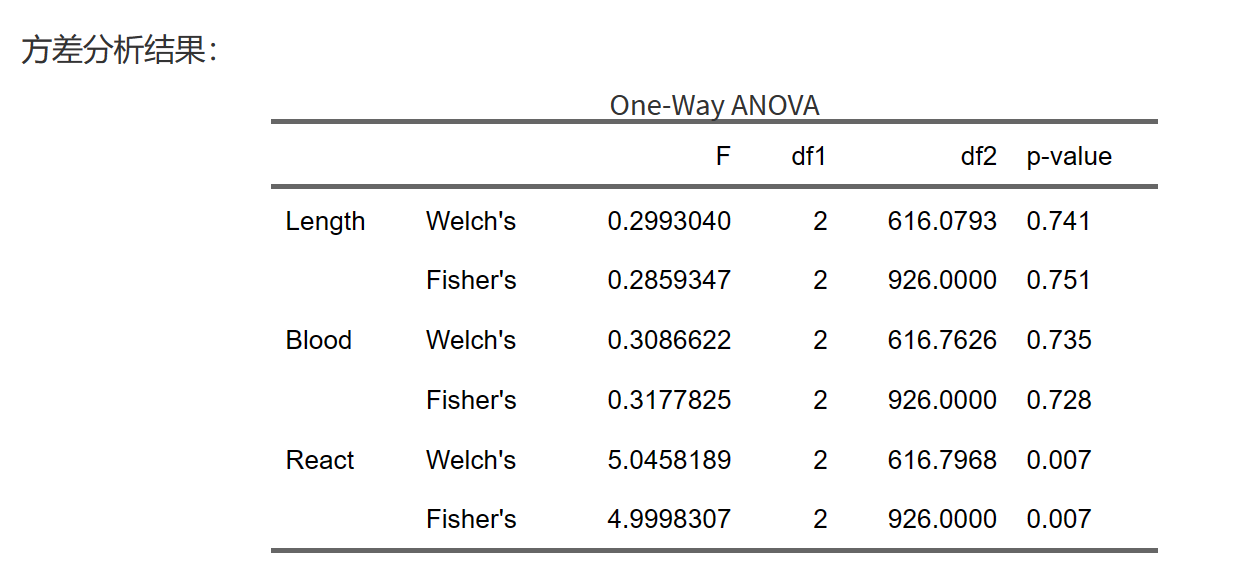
- 方差分析的方法:可选 Welch’s 法(方差不齐)和 Fisher’s 法(方差齐);
- 事后检验:对各组进行两两比较,包括Games-Howell (方差不齐) 法和Tukey法(方差齐)

9.12.1 准备数据
到导入数据页面下载示例数据看一下:
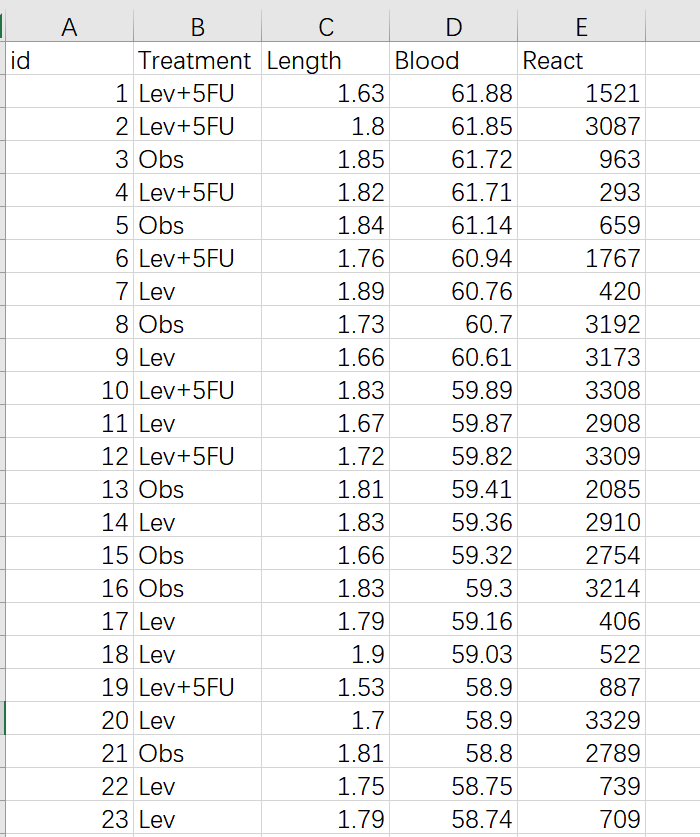
Treatment是代表治疗组别的变量,这里有三个组Lev, Obs, 和Lev+5FU组。需要把变量属性设置成factor
Length, Blood 和React是代表效果的变量,为连续性变量。需要把变量属性设置成numeric
单因素方差分析,主要看 三个组中,Length, Blood 或React 的均值是否相同。
另外可以进行事后分析,分别看上述指标在Lev vs. Obs, Lev vs. Lev+5FU, Obs vs. Lev+5FU对比中的差异。
9.12.2 开始方差分析
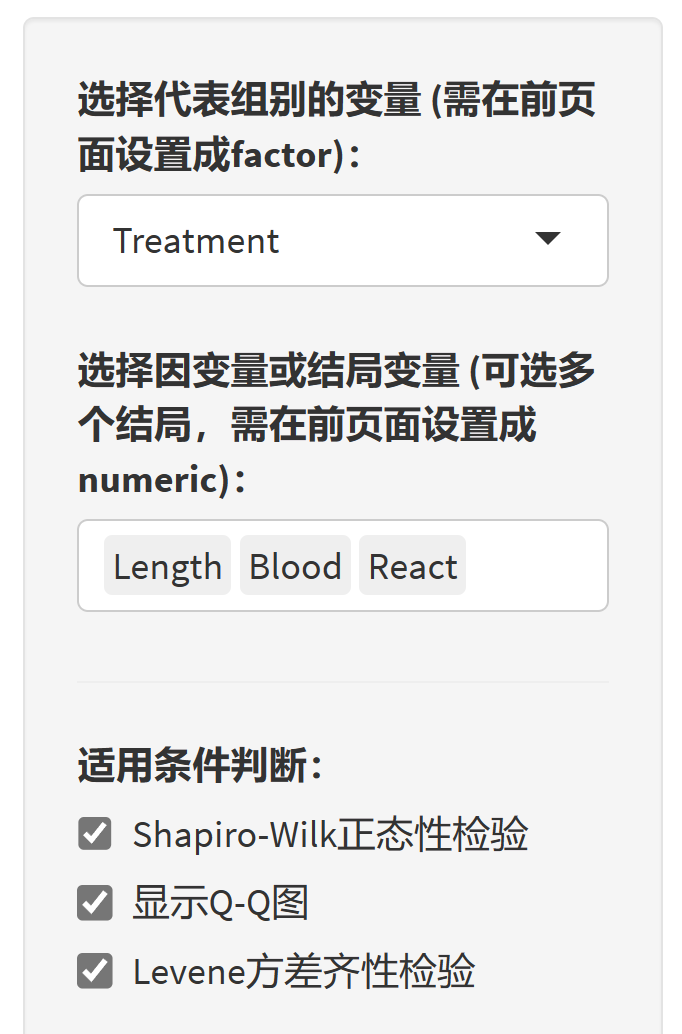
选择代表组别的变量,如果菜单里没有,则返回去把你想要的组别变量设置为factor
选择因变量,这里一次可以分析多个因变量,如果菜单里没有你想要的变量,则返回去把它设置成numeric
9.12.5 描述性分析
然后可以做一下描述性分析:
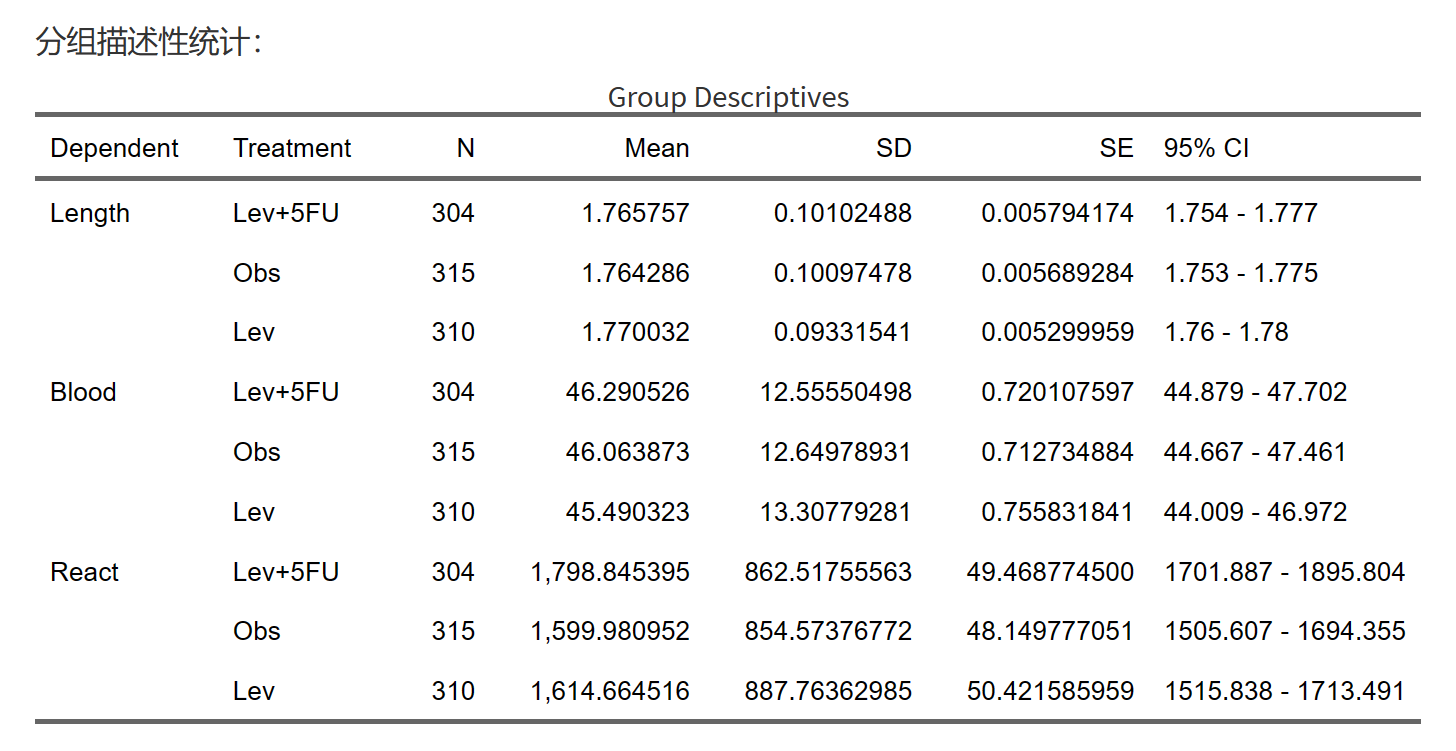
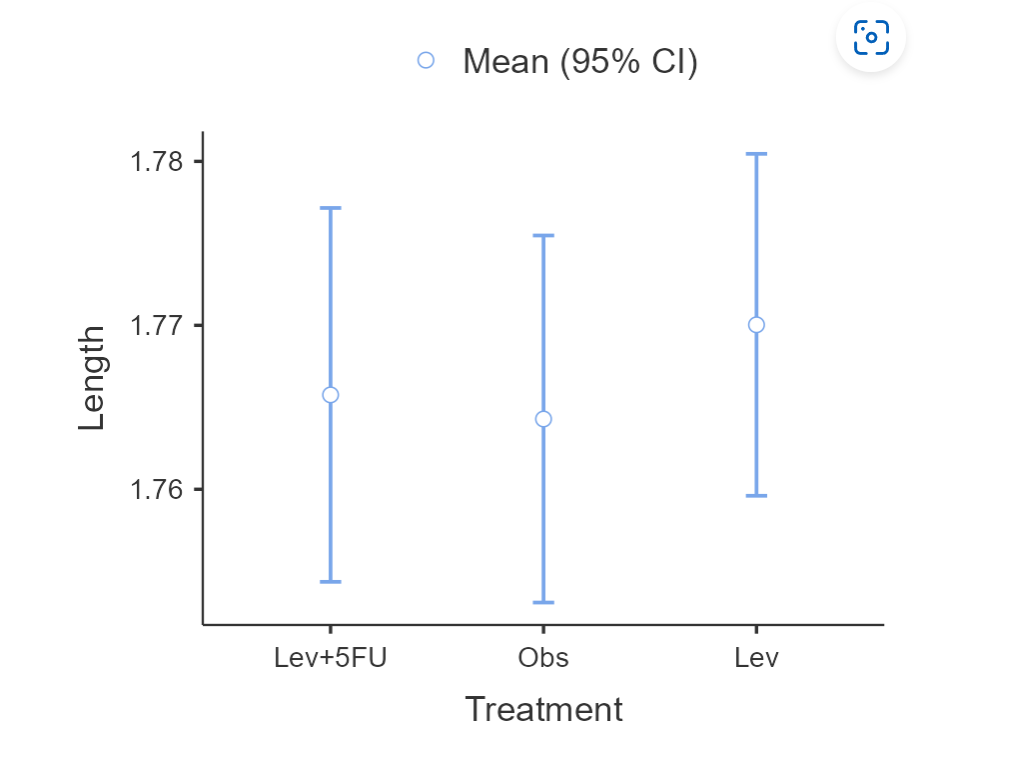
然后可以根据方差齐性的结果,选择方差分析的方法。
对于不是特别严重的方差不齐,单因素方差分析提供了校正检验方法(Welch one-way ANOVA/ Welch’s F检验),考虑了方差差异之后的更为稳健的分析结果。但当组间方差差异较大时,校正结果也不一定可信,建议使用非参数检验(Kruskal-Wallis检验)。如果数据正态性和方差齐性都不满足,最好使用非参数检验(Kruskal-Wallis检验)。
9.12.6 事后检验(两两比较)
但组别为三个及以上时,方差分析的结果只能告诉我们,多组之间的均值是否全相等或不全相等,还不能告诉我们每个组两两比较的结果。
这时候可以用事后分析做两两比较。可以根据方差齐性检验的结果来决定用Games-Howell (方差不齐) 法和Tukey法(方差齐)做事后分析。
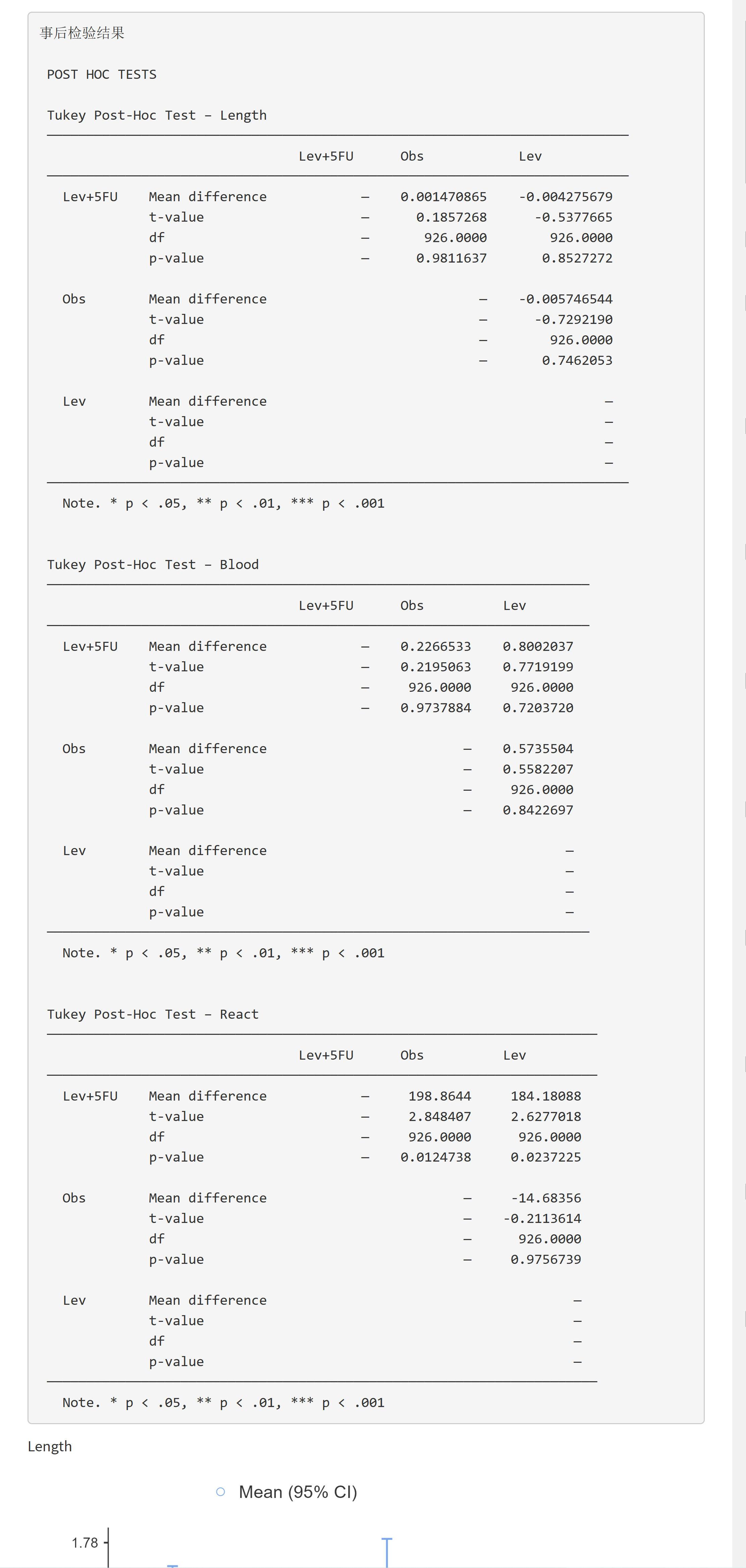
9.12.8 讨论:
严格来讲,单因素方差分析时,需要分别对每一组数据的正态性进行检验。但方差分析对数据非正态性具有一定的耐受力,如果数据不是严重偏态或者只有部分组别数据不满足正态性要求,出于参数检验的统计学效能优于非参数检验的角度,还是可以使用单因素方差分析方法,而不使用非参数检验。
本软件在”单因素方差分析”和”方差分析”模块下的”适用条件判断”中均提供了”正态性检验”和”绘制Q-Q图”功能可检验数据的正态性情况,但此处检验的是数据的整体正态分布(感兴趣的读者请自行操作)。正如上所述,单因素方差分析对数据非正态性具有一定的耐受力,如果数据满足整体正态分布,也是可以使用该种分析方法。但我们建议尽可能分组别检验数据的正态性。
对于不是特别严重的方差不齐,单因素方差分析提供了校正检验方法(Welch one-way ANOVA/ Welch’s F检验),考虑了方差差异之后的更为稳健的分析结果。但当组间方差差异较大时,校正结果也不一定可信,建议使用非参数检验(Kruskal-Wallis检验)。如果数据正态性和方差齐性都不满足,最好使用非参数检验(Kruskal-Wallis检验)。
多重比较一般分为事前检验(Prior tests)和事后检验(Post hoc tests)。事前检验是指在数据收集之前便决定了要通过多重比较来考察多个组与某个特定组之间的差别,多根据专业意义设定比较的策略。如果是事前检验,不论整体分析的结果如何,均可进行比较,并且一般不需要对检验水准进行太多修正。事后检验只有在方差分析得到有统计学意义的F值后才有必要进行,是一种探索性分析。对于事先未计划的多重比较(即事后检验),各组间的差别只是一种提示,要确认这种差别最好重新设计实验。
本软件在”单因素方差分析”和”方差分析”模块下的”事后检验”中均提供了多重比较的方法。“单因素方差分析”方法下的事后检验提供了”Games-Howell (unequal variances)“法和”Tukey (equal variances)“法两种方法,前者为方差不齐时使用,后者为方差齐时使用。
如果还不够,可以移步”方差分析”模块:
“方差分析”模块下的事后检验提供了”Tukey”法、“Scheffe”法、“Bonferroni”法和”Holm”法四种方法,均为在方差齐时使用。其中”Bonferroni”法为对检验水准的严格校正,校正后的检验水准为原始检验水准除以比较次数,当两两比较的次数较多时,结果偏保守。“Holm”法对检验水准的校正程度不如”Bonferroni”法严格,结果更为稳健。Scheffe法的检验效能优于Bonferroni法。Tukey法使用时需要样本数目相同,并可能产生较多的假阴性结果。
9.13 方差分析(ANOVA)
当有两个或者两个以上的因素对因变量产生影响时,可以用多因素方差分析的方法来进行分析。多因素方差分析亦称”多向方差分析”,原理与单因素方差分析基本一致,也是利用方差比较的方法,通过假设检验的过程来判断多个因素是否对因变量产生显著性影响。在多因素方差分析中,由于影响因变量的因素有多个,其中某些因素除了自身对因变量产生影响之外,它们之间也有可能会共同对因变量产生影响。在多因素方差分析中,把因素单独对因变量产生的影响称之为”主效应”;把因素之间共同对因变量产生的影响,或者因素某些水平同时出现时,除了主效应之外的附加影响,称之为”交互效应”。多因素方差分析不仅要考虑每个因素的主效应,往往还要考虑因素之间的交互效应。
两因素方差分析原理如下,两个以上因素也同理:

多因素方差分析,需要满足6个条件:
条件1:观察变量唯一,且为连续变量。
条件2:有多个分组变量,且都为分类变量。
条件3:观测值相互独立。
条件4:观察变量不存在显著的异常值。
条件5:各组、各水平观察变量为正态(或近似正态)分布。
条件6:相互比较的各处理水平(组别)的总体方差相等,即通过方差齐性检验。
MSTATA 医学科研统计机器人提供了一站式的多因素方差分析步骤:
- 数据是否适合做方差分析:提供正态性检验、QQ图、方差齐性检验;
- 进行多因素方差分析,可选交互作用或不选交互作用
- 事后检验:对各水平亚组进行两两比较,可以调整多重比较的P值,可选Tukey法,Scheffe法,Bonferroni法和Holm法
- 计算效应量(effect size)
- 计算和比较各水平亚组的估计边际平均值(Estimated marginal means)和置信区间,生成统计表,绘制统计图
9.13.1 准备数据
到”导入数据”页面下载示例数据看一下:
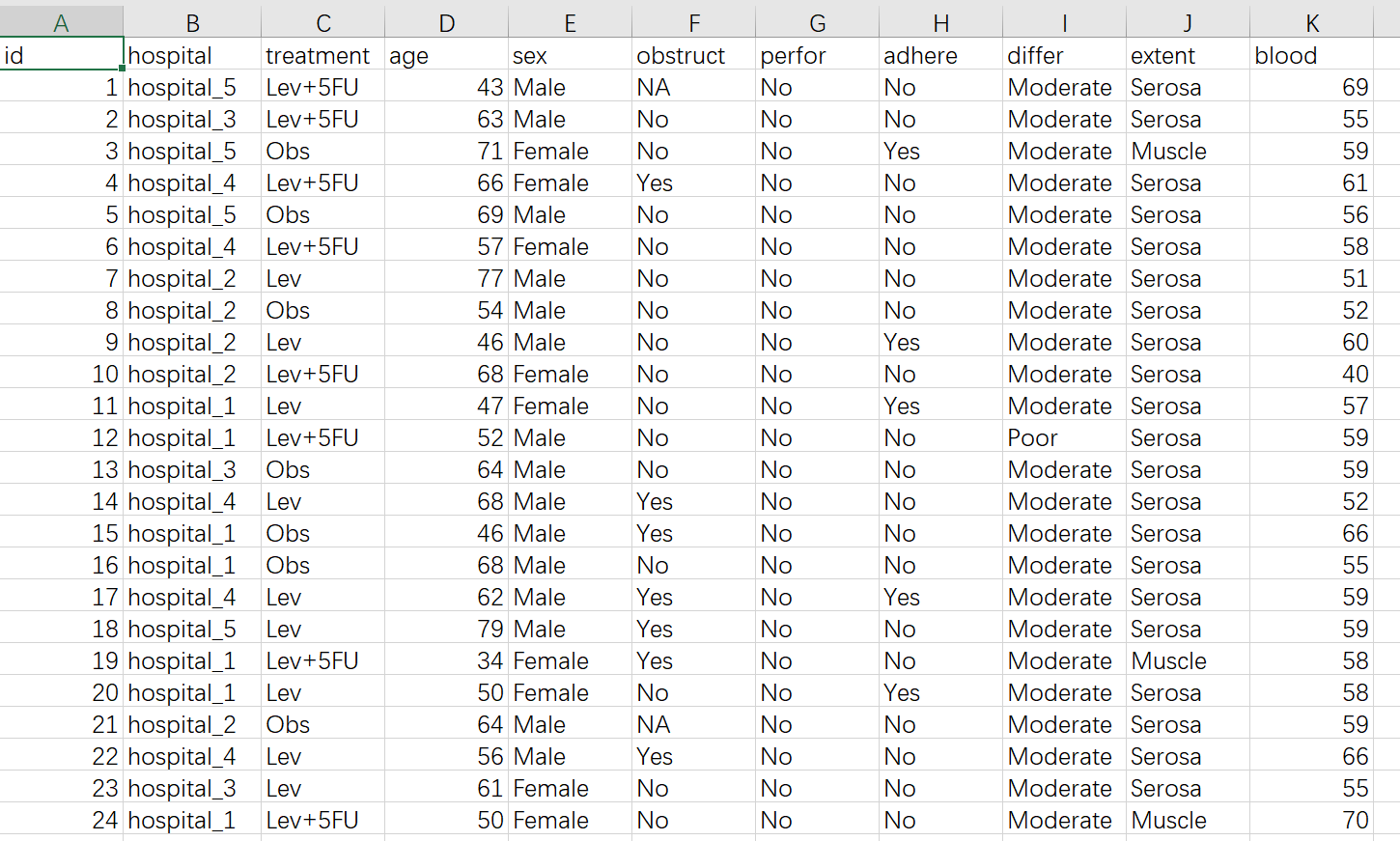
treatment是代表治疗组别的变量,这里有三个组Lev, Obs, 和Lev+5FU组。需要把变量属性设置成factor
blood 是代表结局的变量,为连续性变量。需要把变量属性设置成numeric
其他的分类变量如hospital, sex, obstruct等等,都算是分组处理因素。
探讨blood在不同组别、不同分组处理因素中均值的比较,就是多因素方差分析。
例如做一个两因素方差分析:
blood ~ treatment+sex
其中treatment有三组,sex有两组。
也可以包含交互作用:
blood ~ treatment+sex+treatment:sex
交互作用一般用冒号 : 连接两个变量
其中treatment和sex表示主效应,treatment:sex表示交互效应
如果要探讨三个因素,可以有多种方法:
blood ~ treatment+sex+obstruct 只考虑主效应
blood ~ treatment+sex+obstruct+treatment:sex 考虑一个交互作用
blood ~ treatment+sex+obstruct+treatment:sex+treatment:obstruct+sex:obstruct+treatment:sex:obstruct 考虑所有交互作用
9.13.3 开始方差分析
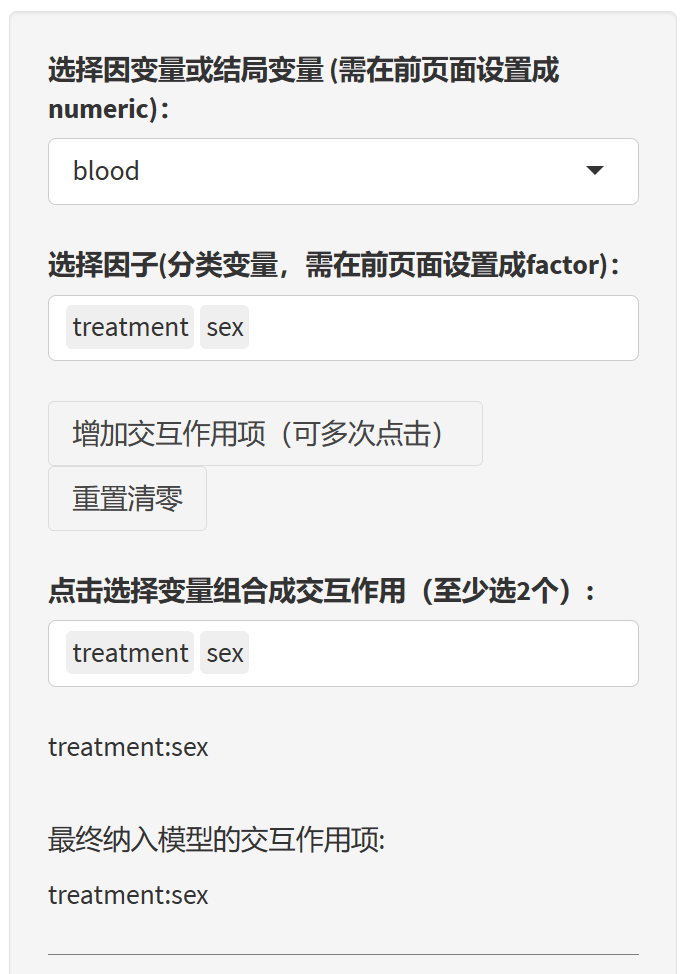
选择因变量,只能选择一个,如果菜单里没有你想要的变量,则返回去把它设置成numeric
选择代表组别的因子,这里我们选treatment和sex,如果菜单里没有,则返回去把你想要的组别变量设置为factor
选择交互作用,每点击一次”增加交互作用项”按钮,就可以增加一个交互作用项菜单,在菜单里选两个以上的变量,就能将其合成交互作用项。这里我们合成一个treatment:sex。如果选错了要修改,可以点击”重置清零”按钮。
9.13.4 使用条件判断
这里可以勾选正态性检验和方差齐性检验等。

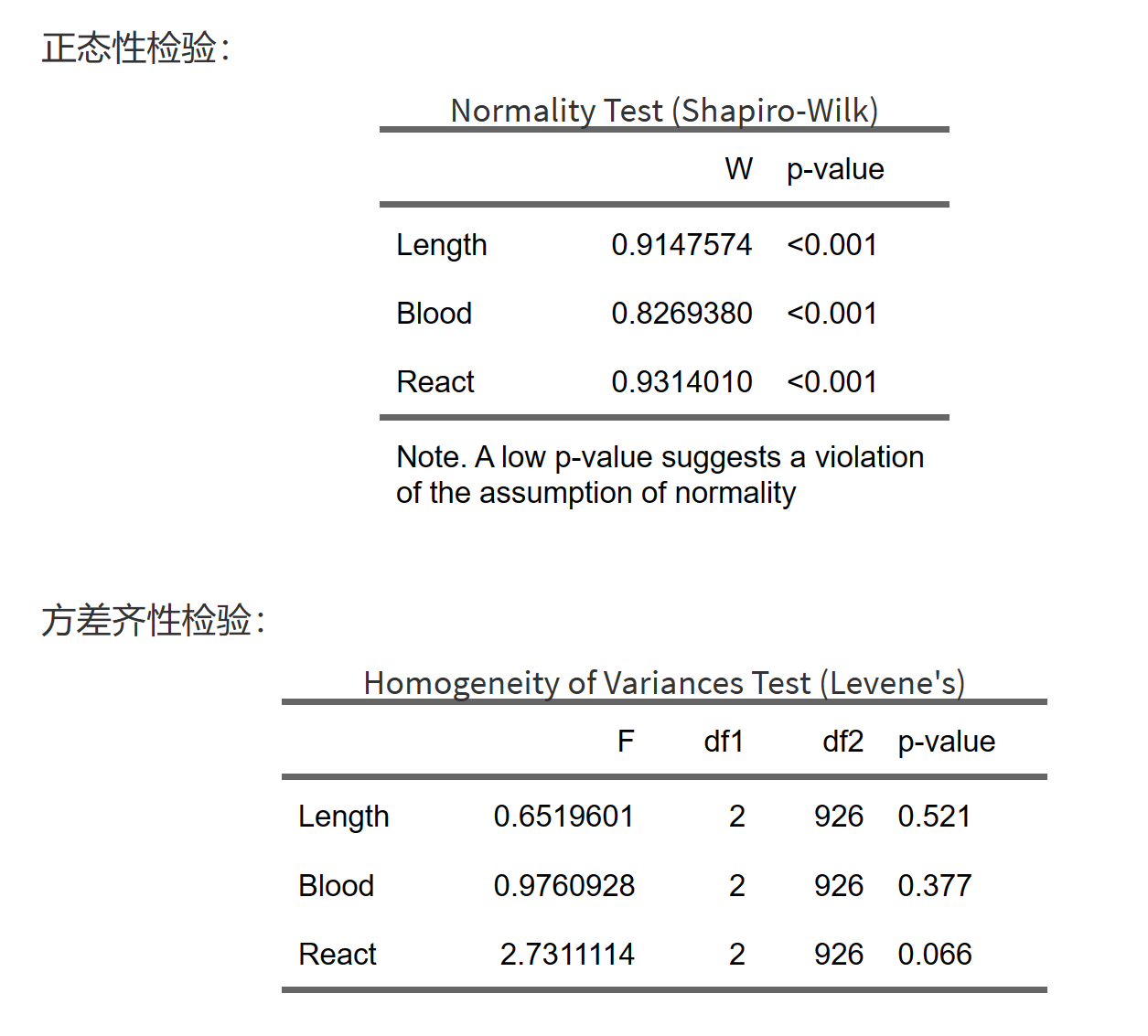
检验结果如下:
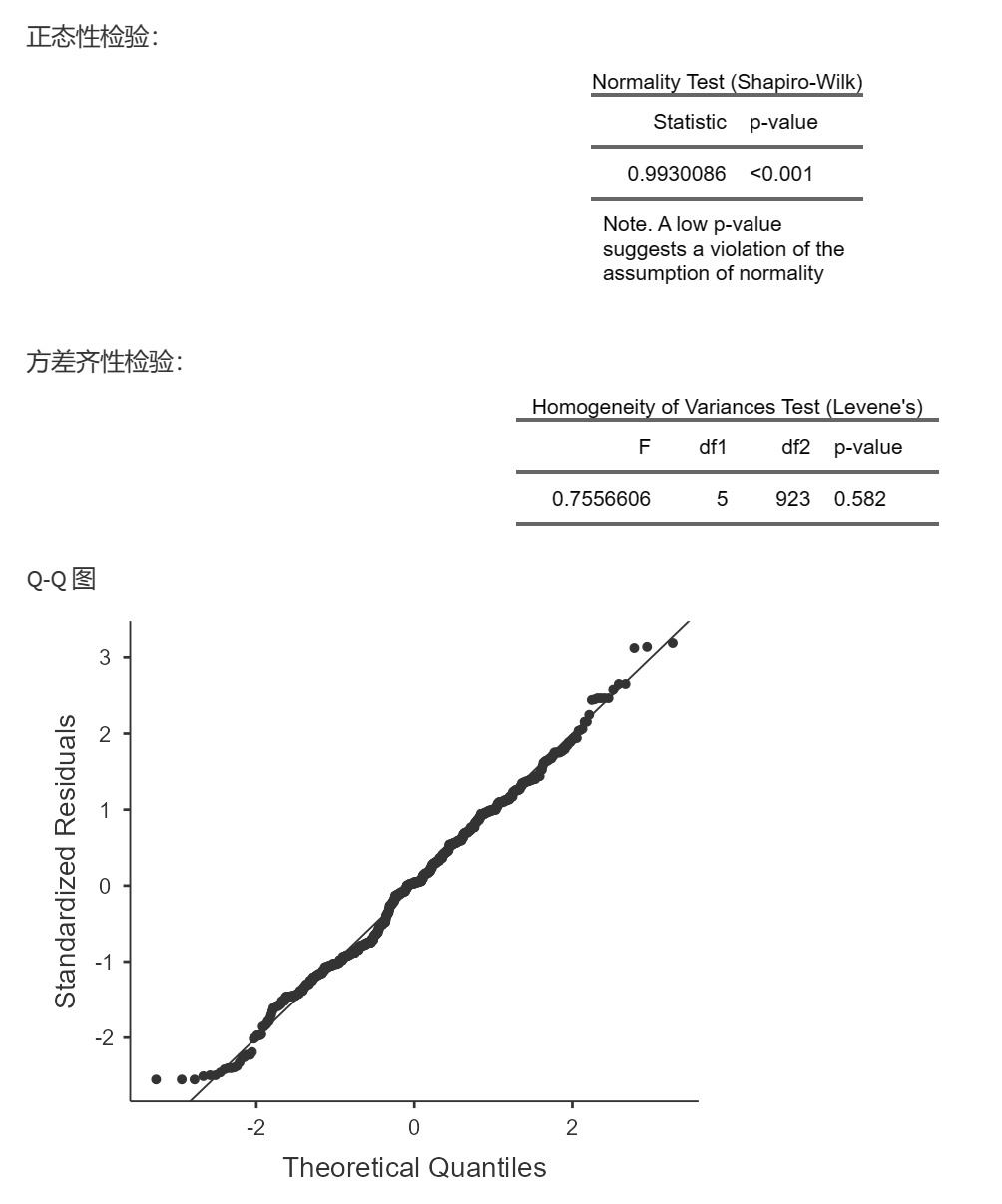
正态性检验仅供参考,P<0.05提示正态性不好,但即使正态性不佳,也可以做方差分析;
方差齐性检验,P<0.05时提示可能方差不齐;
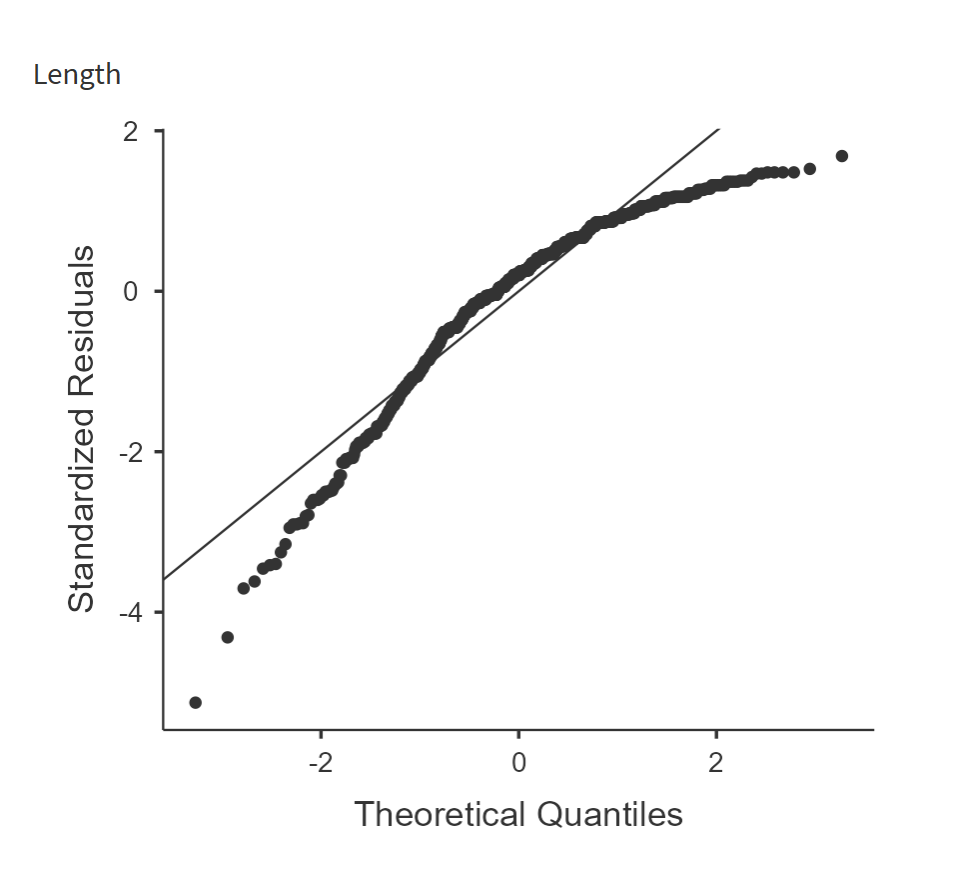
Q-Q图是针对标准化残差做的,如果不太偏离这条直线,说明残差呈正态分布,可以做方差分析。
如果都不满足,可以考虑给因变量取对数或开平方后,再进行检测和做方差分析,
如果还不行,考虑非参数检验。
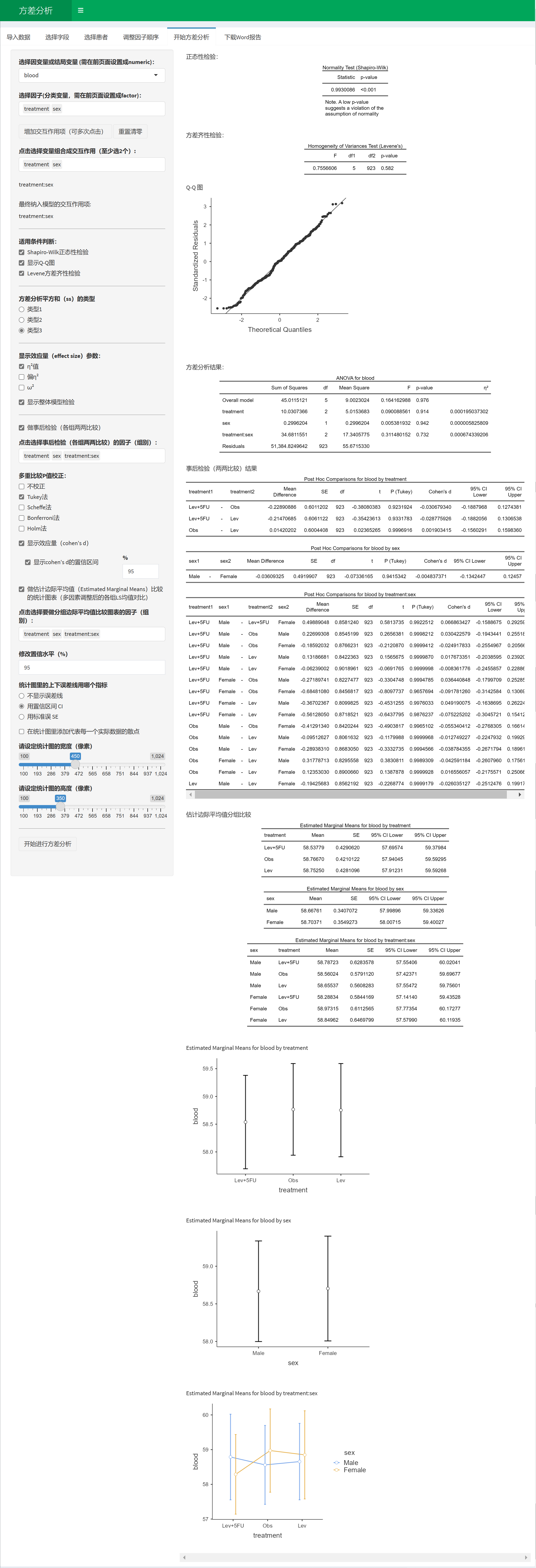
9.13.5 方差分析的选项

这里可以选择平方和(ss)的类型,默认选类型3;
可以选择是否计算effect size, 这里给了常见的三个参数;
也可以选择是否显示整体模型检验的参数
分析结果:
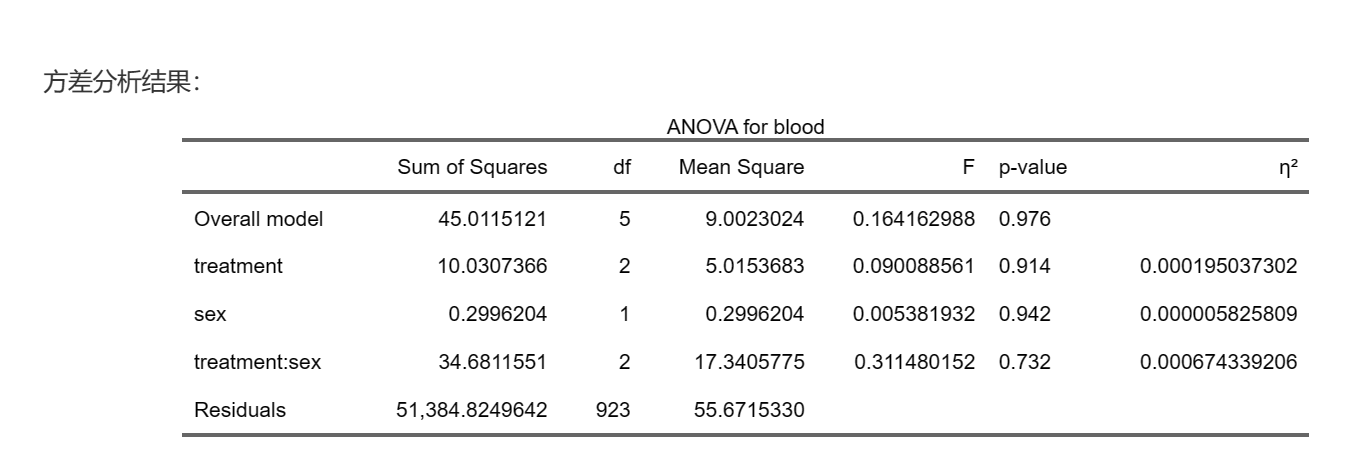
这里根据前面的选择,对treatment、sex以及它们的交互作用进行了方差分析,显示了平方和、均方、F值和P值,这里P值小于0.05表示该因素不同水平的blood均值的差异有统计学意义。而effect size则客观描述了标化量纲之后的效应大小。
9.13.6 事后检验
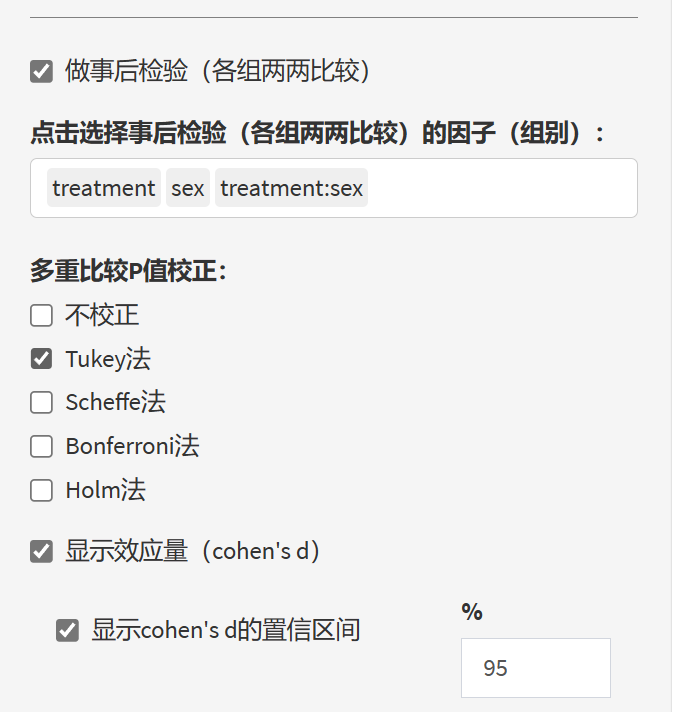
如果有些因子有三个组或以上,如这里的treatment就有三个组,则可以选择做事后检验进行两两比较。
三个组以上两两比较时,需要对P值进行校正,这里提供了Tukey法,Scheffe法,Bonferroni法和Holm法;如果只有两个组,则校正和不校正的P值没有区别。
另外,可选计算cohen’s d效应量及其置信区间。
事后检验的结果如下:
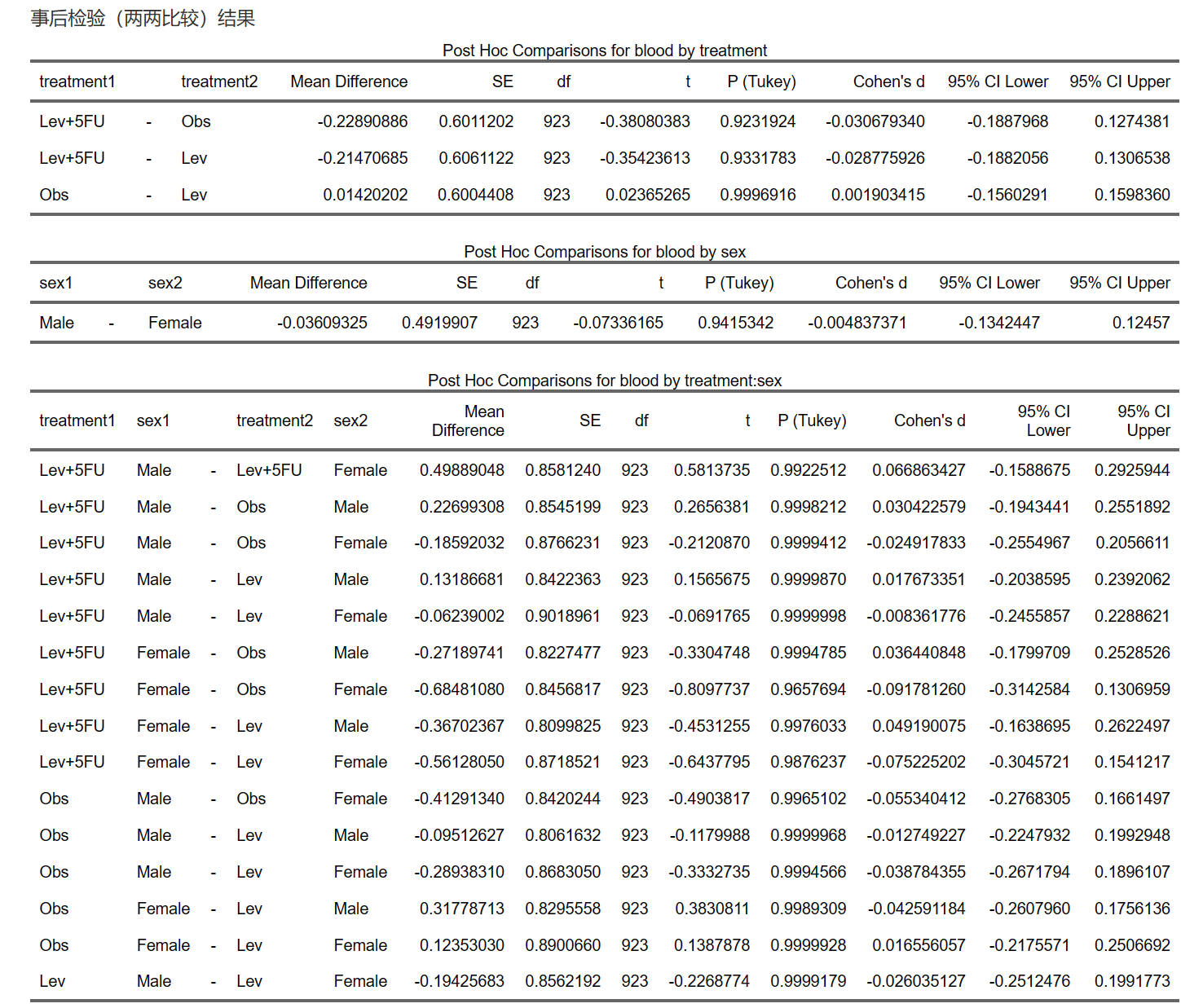
事后检验比较重要的参数是两组之间的差值Mean Difference (adjusted) 和SE,以及调整后的P值。
注意:表里的95% CI是Cohen’s d的可信区间,不是Mean Difference的可信区间。
9.13.7 估计边际平均值
所谓边际均值,就是在控制了其他因素之后,只是单纯在一个因素的作用下,因变量的变化。
举个简单的例子,如果只有一个自变量时,计算出来的边际均值和普通均值是一样的;当有两个及以上自变量时,计算边际均值和普通均值的出来的结果是不同的。
点击勾选需要计算边际均值的分组变量,交互作用也可以选。
分析结果如下:
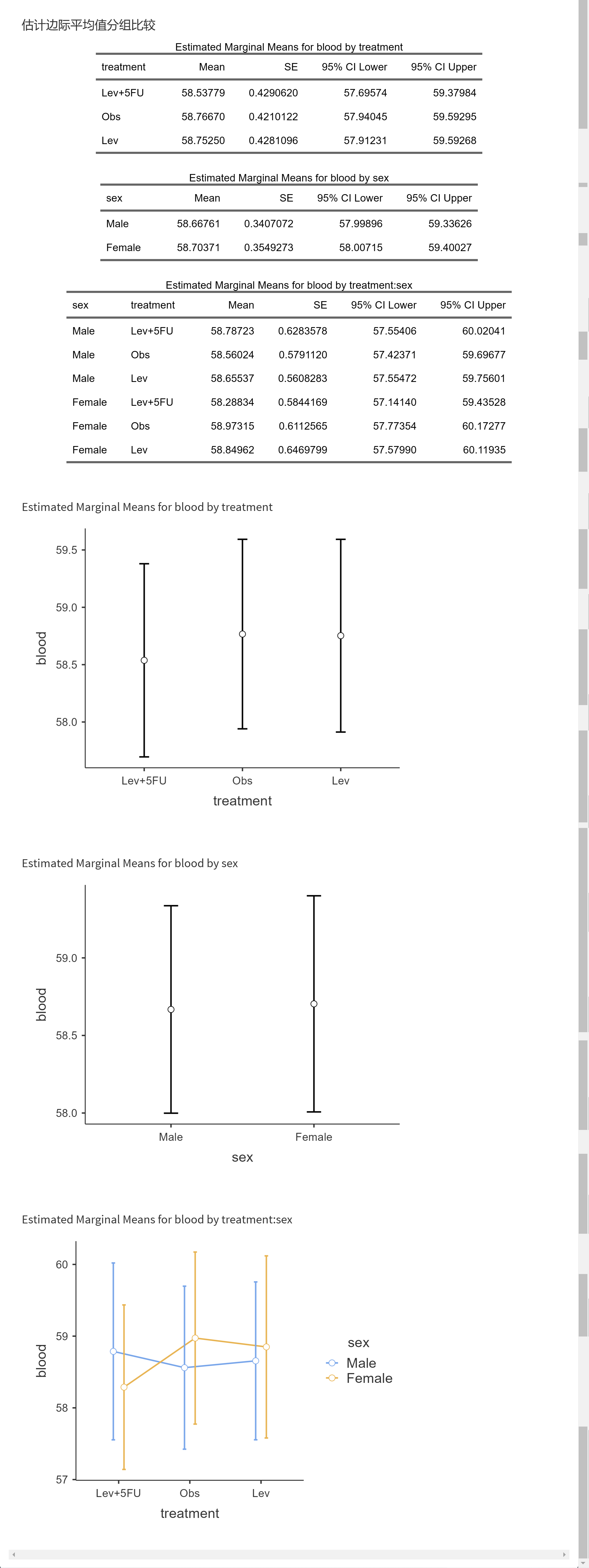
这里的统计图,上下两条误差线可以用SE,也可以用置信区间表示。
统计表的解读:
例如三个治疗组,Lev+5FU、Obs、Lev 各自的blood边际均值和95% CI都可以在第一个表中找到;
两个性别,Female 和 Male各自的blood边际均值和95% CI可以在第二个表中找到;
而第三个表,交互作用表中,则有3*2=6个亚组,如男性接受Lev+5FU治疗组,blood边际均值为58.79
统计图的解读:
中间的圆点是均值,上下两条线是误差线。
在最后一个交互作用图中,横坐标是treatment, 图例分组是sex, 如果想颠倒过来,在选择边际均值项的菜单中,可以先选sex, 再选treatment, 图像的交叉顺序是根据菜单选择顺序来排列的。treatment:sex和sex:treatment在图像排列上有所不同。
9.13.9 讨论
方差分析对数据非正态性具有一定的耐受力,如果数据不是严重偏态或者只有部分组别数据不满足正态性要求,出于参数检验的统计学效能优于非参数检验的角度,还是可以使用方差分析方法,而不使用非参数检验。
多重比较一般分为事前检验(Prior tests)和事后检验(Post hoc tests)。事前检验是指在数据收集之前便决定了要通过多重比较来考察多个组与某个特定组之间的差别,多根据专业意义设定比较的策略。如果是事前检验,不论整体分析的结果如何,均可进行比较,并且一般不需要对检验水准进行太多修正。事后检验只有在方差分析得到有统计学意义的F值后才有必要进行,是一种探索性分析。对于事先未计划的多重比较(即事后检验),各组间的差别只是一种提示,要确认这种差别最好重新设计实验。
事后检验提供了”Tukey”法、“Scheffe”法、“Bonferroni”法和”Holm”法四种方法,均为在方差齐时使用。其中”Bonferroni”法为对检验水准的严格校正,校正后的检验水准为原始检验水准除以比较次数,当两两比较的次数较多时,结果偏保守。“Holm”法对检验水准的校正程度不如”Bonferroni”法严格,结果更为稳健。Scheffe法的检验效能优于Bonferroni法。Tukey法使用时需要样本数目相同,并可能产生较多的假阴性结果。
9.14 协方差分析(ANCOVA)
协方差分析(ANCOVA)是一种统计方法,结合了方差分析(ANOVA)和回归分析的特点。它主要用于比较两个或多个组间的因变量均值差异,在控制一个或多个协变量的影响后。协变量是可能影响因变量的其他变量。通过引入协变量,我们可以减少误差变异,从而更准确地评估组间因变量均值的差异。
以下是一个医学研究中应用协方差分析的例子:
假设我们要研究两种不同药物(药物A和药物B)对降低血压的效果。我们把病人分为两组,一组使用药物A,另一组使用药物B。研究期间,我们还记录了病人的年龄,因为年龄可能会影响血压水平。 在这个例子中,我们的因变量是血压降低的程度,自变量是药物类型(药物A和药物B),协变量是病人的年龄。我们想要比较在控制年龄因素后,药物A和药物B在降低血压方面是否存在显著差异。
我们进行协方差分析(ANCOVA),把年龄设置为协变量,比较调整后的血压降低数值在药物A和药物B组间是否存在显著差异。如果结果显示存在显著差异,我们可以得出结论,在控制年龄因素后,药物A和药物B对降低血压的效果具有显著差异。
通过协方差分析(ANCOVA),我们可以更准确地评估药物A和药物B对降低血压的效果,排除年龄等潜在混杂因素的干扰。这对于医学研究以及其他涉及多个影响因素的领域非常有价值。协方差分析有助于提高研究的准确性和可靠性,使得研究结果更具有说服力。
在实际应用中,协方差分析还可以用于教育、心理学、生态学、经济学等多个学科。例如,在教育研究中,我们可能想要比较两种不同的教学方法对学生学术成绩的影响,同时控制学生的家庭背景等因素。在这种情况下,协方差分析可以帮助我们更准确地评估不同教学方法的效果。
总之,协方差分析是一种强大的统计工具,可以帮助研究人员在控制潜在协变量的影响下,准确评估不同组间因变量均值的差异。
MSTATA 医学科研统计机器人提供了一站式的协方差分析步骤:
- 数据是否适合做方差分析:提供正态性检验、QQ图、方差齐性检验;
- 进行协方差分析,设置因变量和感兴趣的因子,可选交互作用或不选交互作用,设置要调整的协变量;
- 事后检验:对各水平亚组进行两两比较,可以调整多重比较的P值,可选Tukey法,Scheffe法,Bonferroni法和Holm法
- 计算效应量(effect size)
- 计算和比较各水平亚组的估计边际平均值(Estimated marginal means)和置信区间,生成统计表,绘制统计图
9.14.1 准备数据
到”导入数据”页面下载示例数据看一下:

treatment是代表治疗组别的变量,这里有三个组Lev, Obs, 和Lev+5FU组。需要把变量属性设置成factor
sex是性别,也是我们感兴趣的组别变量
blood 是代表结局的变量,为连续性变量。需要把变量属性设置成numeric
其他的分类变量如hospital, obstruct等等,我们不感兴趣,只做调整用的协变量。
其他的连续性变量如age, 我们不感兴趣,为协变量。
探讨blood在调整其他协变量后,在不同治疗组、不同性别的均值的比较,就是协方差分析。
9.14.3 开始协方差分析
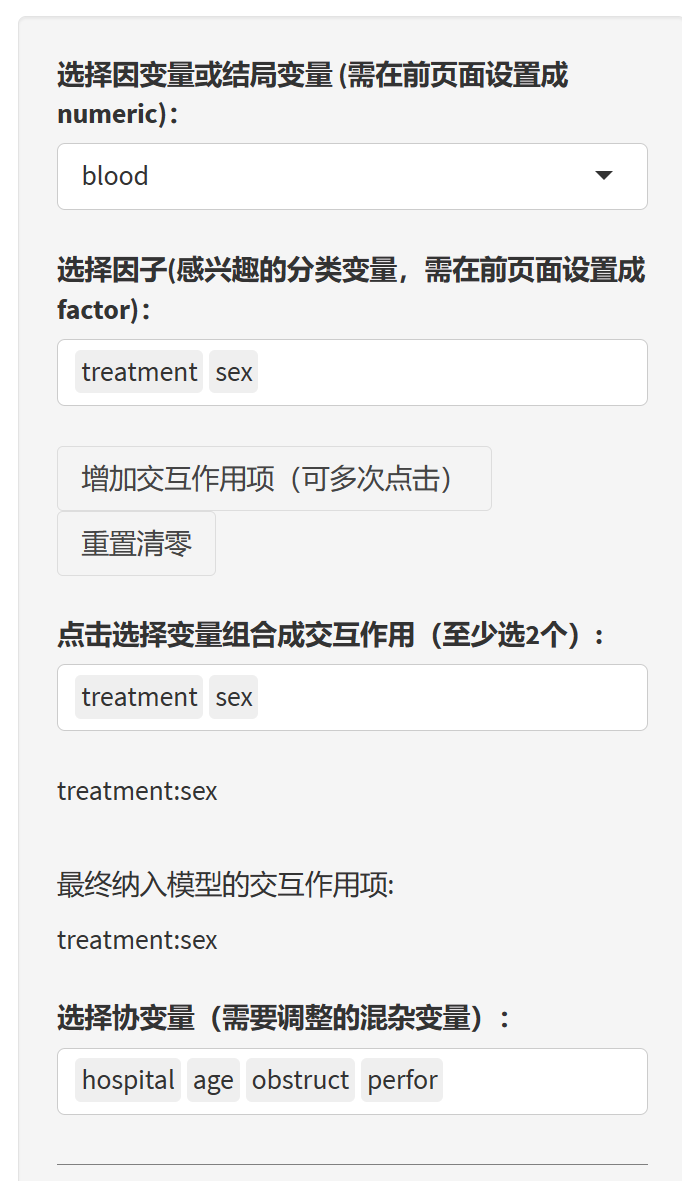
选择因变量,只能选择一个,如果菜单里没有你想要的变量,则返回去把它设置成numeric
选择代表感兴趣的组别的因子,这里我们选treatment和sex,如果菜单里没有,则返回去把你想要的组别变量设置为factor
选择交互作用,每点击一次”增加交互作用项”按钮,就可以增加一个交互作用项菜单,在菜单里选两个以上的变量,就能将其合成交互作用项。这里我们合成一个treatment:sex。如果选错了要修改,可以点击”重置清零”按钮。
选择不感兴趣,用来做调整的协变量:这里hospital, age, obstruct, perfor可能对结局有影响,但不是我们研究感兴趣的研究变量,因此勾选用来做协变量调整。
9.14.4 使用条件判断
这里可以勾选正态性检验和方差齐性检验等。

检验结果如下:
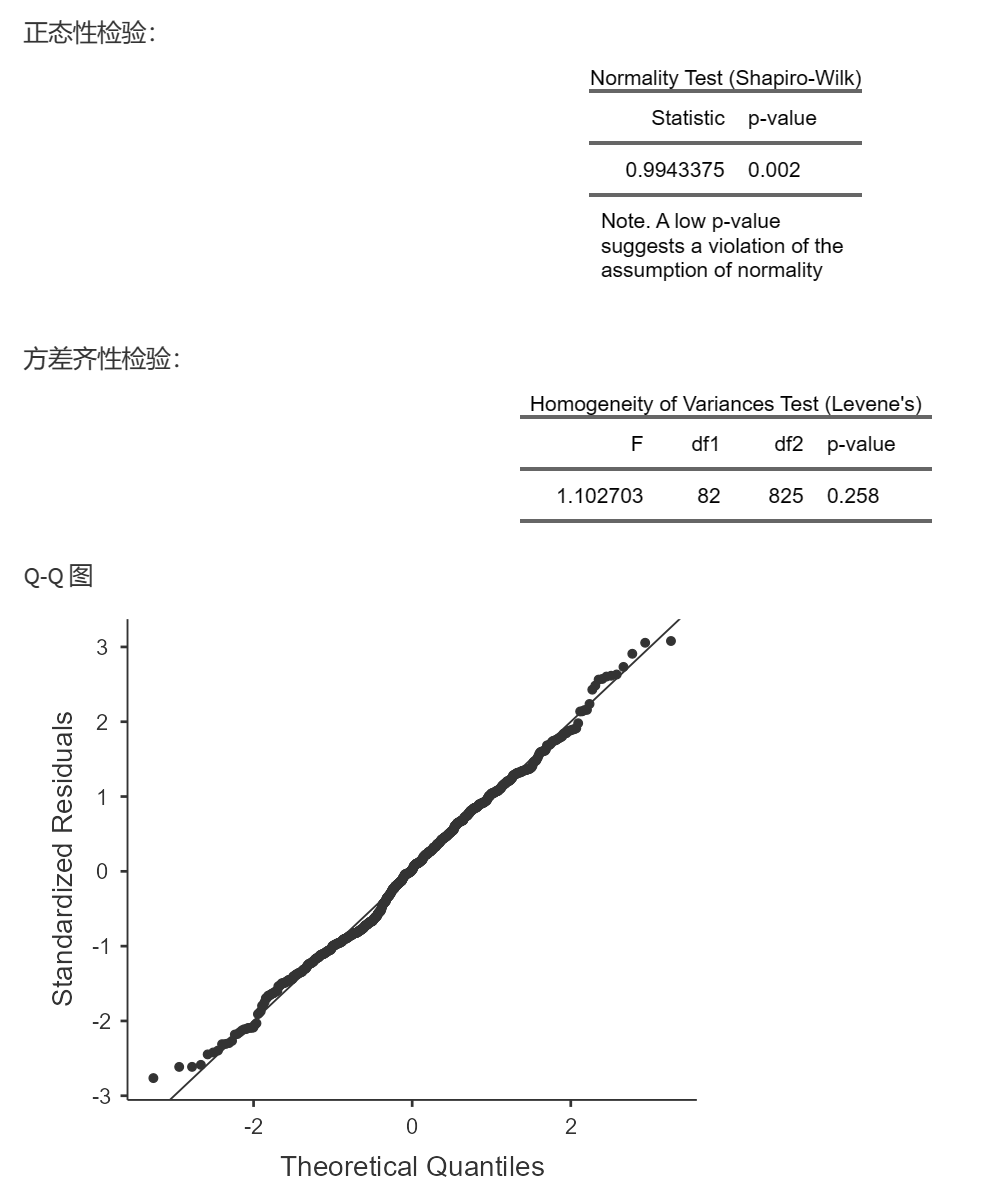
正态性检验仅供参考,P<0.05提示正态性不好,但即使正态性不佳,也可以做方差分析;
方差齐性检验,P<0.05时提示可能方差不齐;
Q-Q图是针对标准化残差做的,如果不太偏离这条直线,说明残差呈正态分布,可以做方差分析。
如果都不满足,可以考虑给因变量取对数或开平方后,再进行检测和做方差分析,
如果还不行,考虑非参数检验。
9.14.5 方差分析的选项

这里可以选择平方和(ss)的类型,默认选类型3;
可以选择是否计算effect size, 这里给了常见的三个参数;
也可以选择是否显示整体模型检验的参数
分析结果:
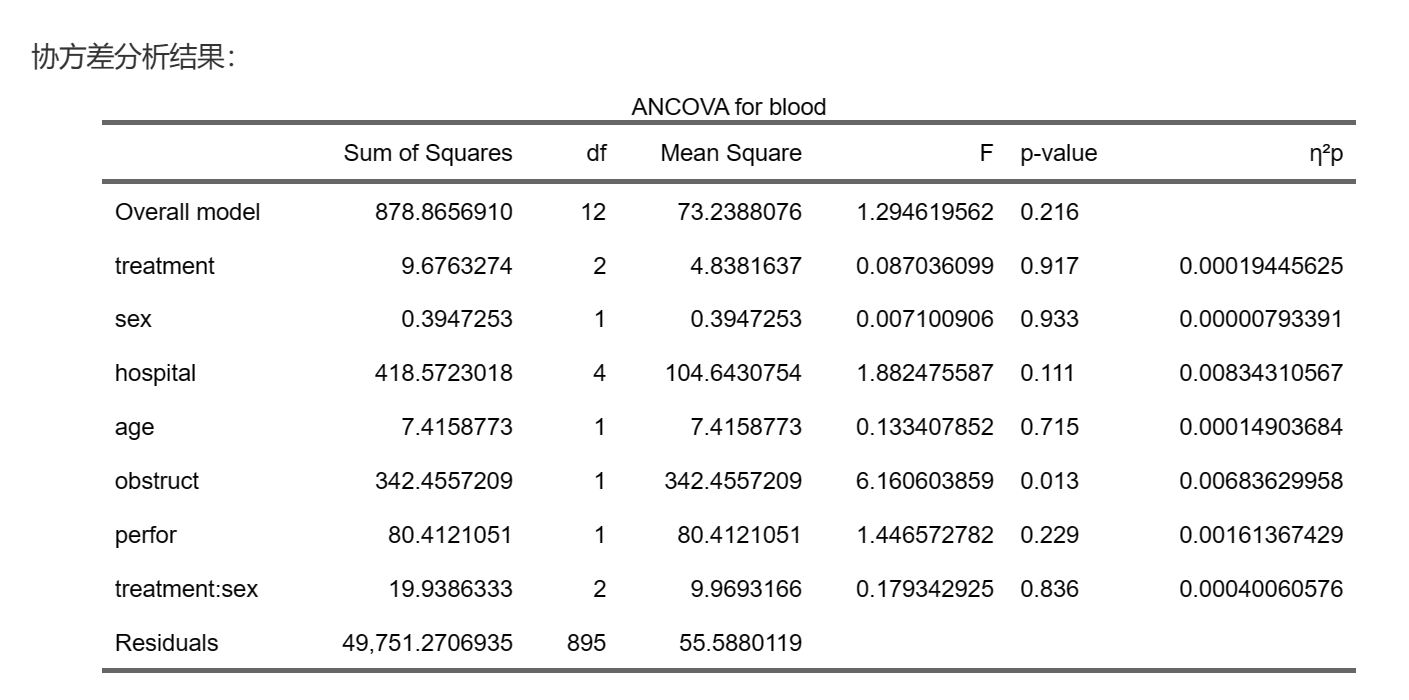
这里根据前面的选择,所选的因子、交互作用和协变量都做了协方差分析,显示了平方和、均方、F值和P值,这里P值小于0.05表示该因素不同水平的blood均值的差异有统计学意义。而effect size则客观描述了标化量纲之后的效应大小。
9.14.6 事后检验

如果有些因子有三个组或以上,如这里的treatment就有三个组,则可以选择做事后检验进行两两比较。
三个组以上两两比较时,需要对P值进行校正,这里提供了Tukey法,Scheffe法,Bonferroni法和Holm法;如果只有两个组,则校正和不校正的P值没有区别。
另外,可选计算cohen’s d效应量及其置信区间。
事后检验的结果如下:
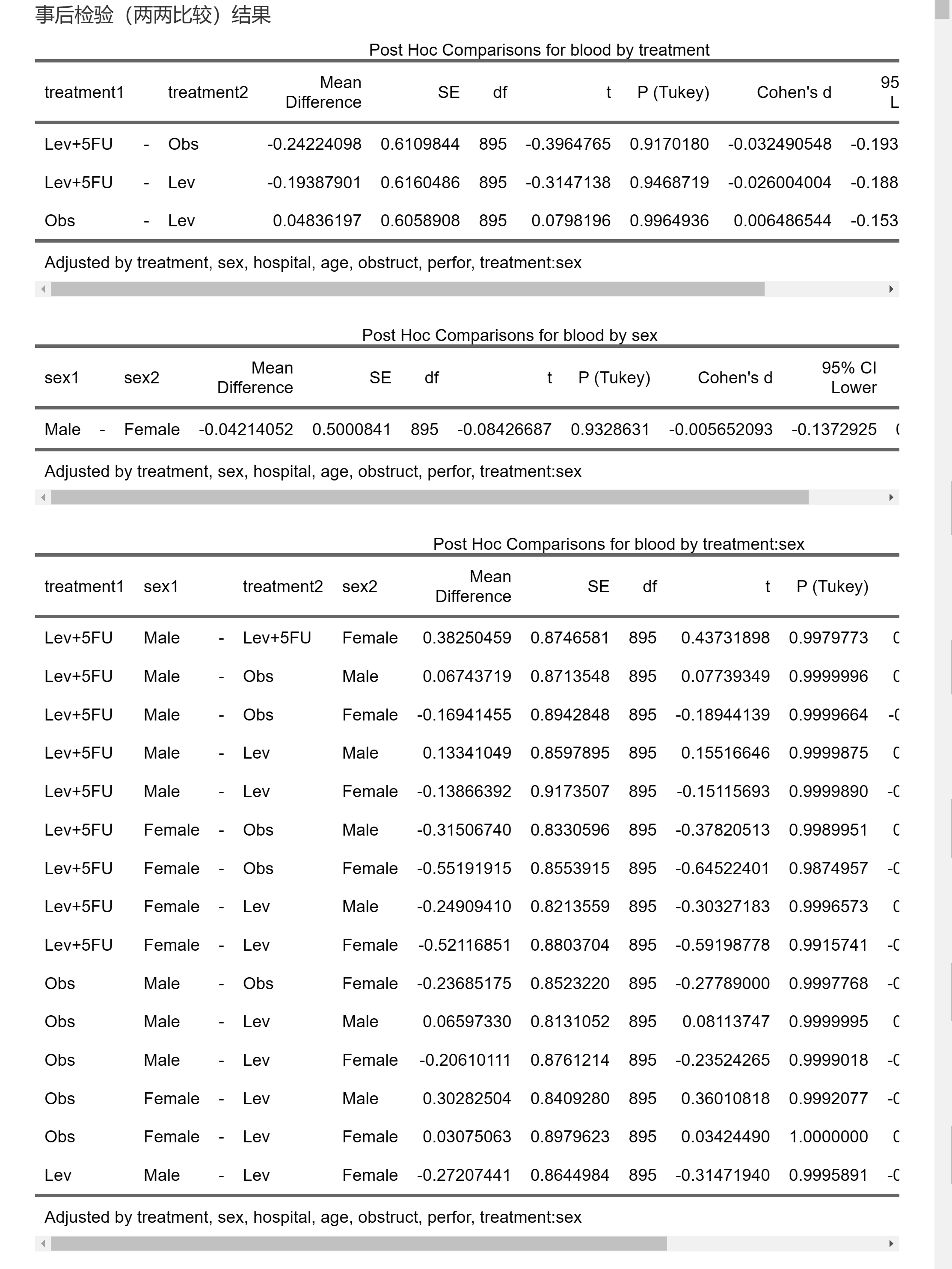
事后检验比较重要的参数是两组之间的差值Mean Difference (adjusted) 和SE,以及调整后的P值。
注意:表里的95% CI是Cohen’s d的可信区间,不是Mean Difference的可信区间。
9.14.7 估计边际平均值

所谓边际均值,就是在控制了其他因素之后,只是单纯在一个因素的作用下,因变量的变化。
举个简单的例子,如果只有一个自变量时,计算出来的边际均值和普通均值是一样的;当有两个及以上自变量时,计算边际均值和普通均值的出来的结果是不同的。
点击勾选需要计算边际均值的分组变量,交互作用也可以选。
分析结果如下:
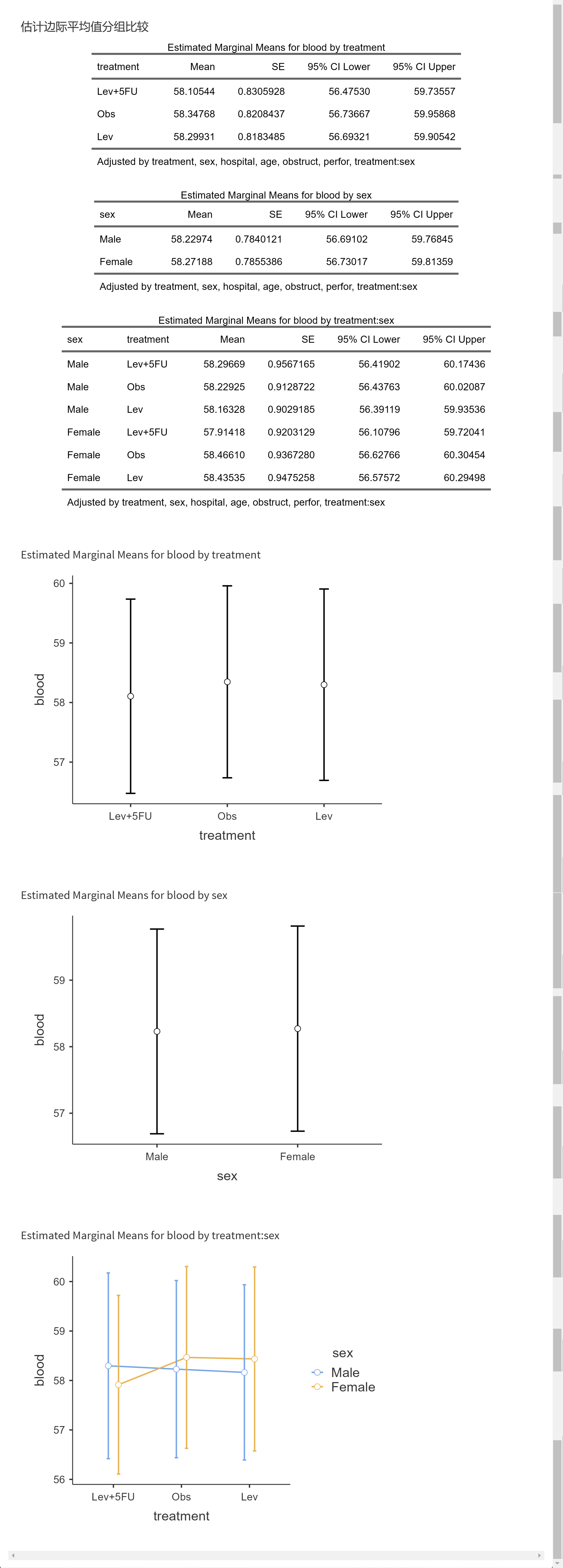

这里的统计图,上下两条误差线可以用SE,也可以用置信区间表示。
统计表的解读:
例如三个治疗组,Lev+5FU、Obs、Lev 各自的blood边际均值和95% CI都可以在第一个表中找到;
两个性别,Female 和 Male各自的blood边际均值和95% CI可以在第二个表中找到;
而第三个表,交互作用表中,则有3*2=6个亚组,如男性接受Lev+5FU治疗组,blood边际均值为58.79
统计图的解读:
中间的圆点是均值,上下两条线是误差线。
在最后一个交互作用图中,横坐标是treatment, 图例分组是sex, 如果想颠倒过来,在选择边际均值项的菜单中,可以先选sex, 再选treatment, 图像的交叉顺序是根据菜单选择顺序来排列的。treatment:sex和sex:treatment在图像排列上有所不同。
9.14.9 讨论
方差分析对数据非正态性具有一定的耐受力,如果数据不是严重偏态或者只有部分组别数据不满足正态性要求,出于参数检验的统计学效能优于非参数检验的角度,还是可以使用方差分析方法,而不使用非参数检验。
多重比较一般分为事前检验(Prior tests)和事后检验(Post hoc tests)。事前检验是指在数据收集之前便决定了要通过多重比较来考察多个组与某个特定组之间的差别,多根据专业意义设定比较的策略。如果是事前检验,不论整体分析的结果如何,均可进行比较,并且一般不需要对检验水准进行太多修正。事后检验只有在方差分析得到有统计学意义的F值后才有必要进行,是一种探索性分析。对于事先未计划的多重比较(即事后检验),各组间的差别只是一种提示,要确认这种差别最好重新设计实验。
事后检验提供了”Tukey”法、“Scheffe”法、“Bonferroni”法和”Holm”法四种方法,均为在方差齐时使用。其中”Bonferroni”法为对检验水准的严格校正,校正后的检验水准为原始检验水准除以比较次数,当两两比较的次数较多时,结果偏保守。“Holm”法对检验水准的校正程度不如”Bonferroni”法严格,结果更为稳健。Scheffe法的检验效能优于Bonferroni法。Tukey法使用时需要样本数目相同,并可能产生较多的假阴性结果。
9.15 多元(协)方差分析(MANCOVA)
多元(协)方差分析(Multivariate Analysis of (Co)Variance,MANCOVA)是一种统计方法,用于研究多个因变量与一个或多个分类和/或连续解释变量之间的关系。与普通(协)方差分析(ANOVA/ANCOVA)相比,MANCOVA能够同时处理多个因变量,从而分析多个相关因变量之间的整体效应。在MANCOVA中,多个因变量被看作是一个整体,并结合在一起进行分析。这有助于检测解释变量对因变量组合的主效应、交互效应以及各组之间的差异。
举例:在心血管疾病患者中,我们研究两种不同药物治疗(药物A和药物B)对生活质量的影响,同时考虑年龄作为一个协变量。生活质量可以通过多个指标来衡量,如心理健康、生理健康和社会功能等。具体指标可以包括:
心理健康:
抑郁程度:如使用汉密尔顿抑郁量表(HAMD)评估;
焦虑程度:如使用汉密尔顿焦虑量表(HAMA)评估;
精神压力水平:例如使用 perceived stress scale(PSS)评估。
生理健康:
心率:静息心率、运动时心率;
血压:收缩压、舒张压;
胆固醇水平:总胆固醇、低密度脂蛋白胆固醇、高密度脂蛋白胆固醇;
身体质量指数(BMI)。
社会功能:
工作能力:例如使用工作能力指数(WAI)评估;
社会支持:例如使用社会支持评定量表(SSRS)评估;
生活满意度:例如使用满意度与生活质量量表(SWLS)评估。
这些指标之间可能存在一定程度的相关性,例如心理健康与生理健康之间可能存在相互影响。使用多元(协)方差分析而不是普通(协)方差分析的原因在于:
多元(协)方差分析能够同时考虑多个因变量,更全面地分析药物治疗对患者生活质量的整体影响。
由于多个指标之间可能存在相关性,多元(协)方差分析能够考虑这些相关性,更准确地评估解释变量和协变量对因变量的影响。
多元(协)方差分析能够检测解释变量对因变量组合的主效应、交互效应以及各组之间的差异,从而为科研工作提供更多信息。
MSTATA做多元(协)方差分析的功能主要有:
适用条件判断:包括Box’s M test(用于检验协方差矩阵的相等性)、Shapiro-Wilk test(用于检验多元正态性)和Q-Q plot of multivariate normality(用于可视化多元正态性)。
使用以下方法进行MANCOVA分析:Pillai’s Trace, Wilks’ Lambda, Hotelling’s Trace和Roy’s Largest Root multivariate statistics。这些方法可以帮助用户确定解释变量对多个因变量的整体影响。
自动生成Word表格,方便用户直接粘贴到论文中。这些表格包括各种统计结果和分析细节,以便用户能够清晰地了解分析过程和结论。
通过MSTATA提供的多元(协)方差分析功能,用户可以方便地对多个因变量进行综合分析,评估解释变量和协变量对因变量的影响,并生成详细的统计报告和可视化结果,从而为科研工作提供有力支持。
9.15.1 准备数据
到”导入数据”页面下载示例数据看一下:
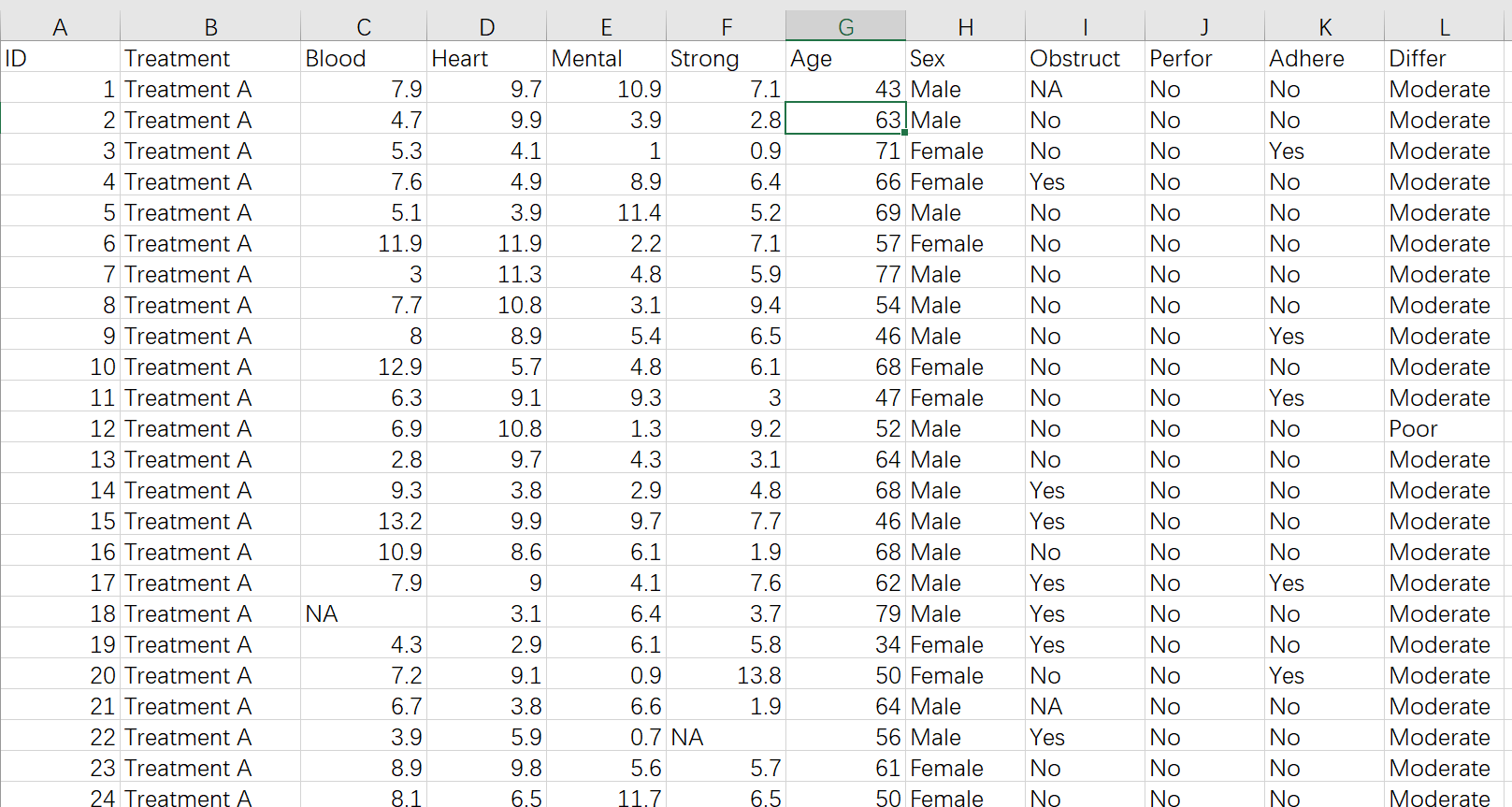
Blood, Heart, Mental, Strong 是一组疗效指标,且有相关性。
treatment是代表治疗组别的变量,这里有三个组Treatment A,Treatment B 和Control组。需要把变量属性设置成factor
sex是性别,也是我们感兴趣的组别变量, 要设为factor
Age是需要调整的协变量,为连续性变量,要设为numeric
9.15.3 开始多元(协)方差分析
选择变量:
选择多个因变量Y,必须是数值型连续变量numeric, 另外选择分组因素自变量facotr,只选感兴趣的分组因素,不要选一大堆。还有协变量numeric。
9.15.4 使用条件判断
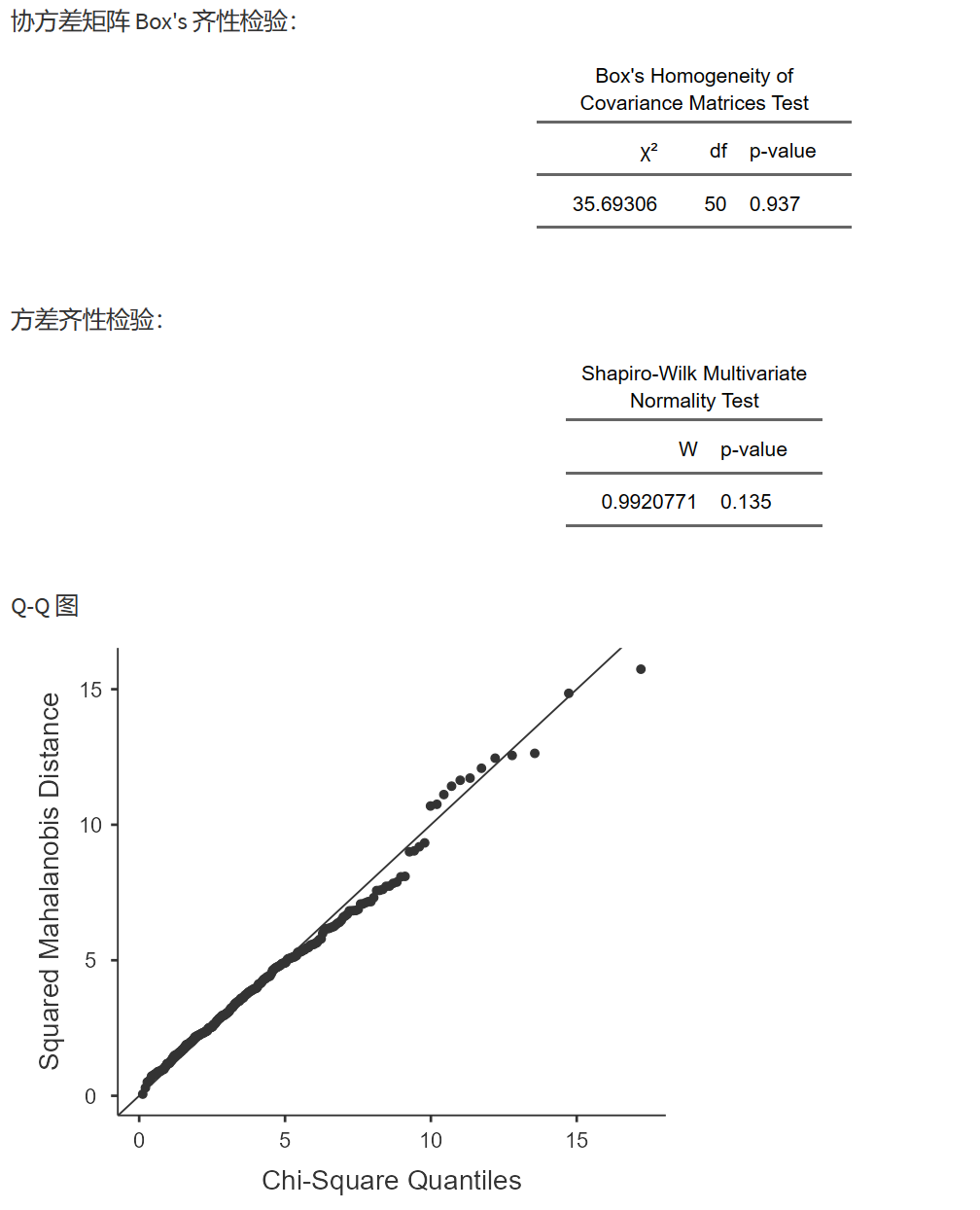
这里可以勾选 Box’s M 检验和多元正态性检验、QQ图等。

多元(协)方差分析(MANCOVA)的适用条件主要包括协方差矩阵相等性、多元正态性和因变量间独立性。以下是相关统计检验的介绍:
- Box’s M 检验:
Box’s M检验用于检验各组协方差矩阵的相等性。协方差矩阵相等性是多元(协)方差分析的基本假设之一。如果各组的协方差矩阵不相等,那么多元(协)方差分析的结果可能受到影响。当Box’s M检验的p值大于显著性水平(如0.05)时,我们不能拒绝原假设(各组协方差矩阵相等),认为满足多元(协)方差分析的要求。
- 显示多元正态Q-Q图:
Q-Q图(Quantile-Quantile图)是一种用于判断样本数据是否符合某种分布(如正态分布)的图形方法。多元正态Q-Q图将多元数据的分位数与理论正态分布的分位数进行比较。如果数据点在Q-Q图上大致沿一条直线排列,则认为数据满足多元正态分布。多元正态性是多元(协)方差分析的另一个基本假设。
- Shapiro-Wilk(正态性)检验:
Shapiro-Wilk检验是一种用于检验样本数据是否符合正态分布的方法。在多元(协)方差分析中,我们需要确保各组因变量满足正态分布。当Shapiro-Wilk检验的p值大于显著性水平(如0.05)时,我们不能拒绝原假设(数据符合正态分布),认为满足多元(协)方差分析的要求。
总之,在进行多元(协)方差分析之前,我们需要满足以下条件:
各组协方差矩阵相等(通过Box’s M检验判断)
数据满足多元正态分布(通过多元正态Q-Q图判断)
如果这些条件得到满足,我们可以认为数据适合进行多元(协)方差分析。
9.15.5 多元(协)方差分析的选项

多元(协)方差分析(MANCOVA)的方法主要有四种,它们分别是Pillai’s Trace、Wilks’ Lambda、Hotelling’s Trace和Roy’s Largest Root。以下是它们的定义以及如何解读结果:
- Pillai’s Trace:
Pillai’s Trace是一种用于检验解释变量对多个因变量的整体影响的方法。其值范围在0到1之间。较大的Pillai’s Trace值表示解释变量对因变量的整体影响较大。通过比较Pillai’s Trace值的观测值与在原假设下的期望值,我们可以得到一个p值,以判断解释变量对因变量组合的影响是否显著。
- Wilks’ Lambda:
Wilks’ Lambda是另一种用于检验解释变量对多个因变量的整体影响的方法。其值范围在0到1之间。较小的Wilks’ Lambda值表示解释变量对因变量的整体影响较大。通过比较Wilks’ Lambda值的观测值与在原假设下的期望值,我们可以得到一个p值,以判断解释变量对因变量组合的影响是否显著。
- Hotelling’s Trace:
Hotelling’s Trace也是一种用于检验解释变量对多个因变量的整体影响的方法。其值大于等于0。较大的Hotelling’s Trace值表示解释变量对因变量的整体影响较大。通过比较Hotelling’s Trace值的观测值与在原假设下的期望值,我们可以得到一个p值,以判断解释变量对因变量组合的影响是否显著。
- Roy’s Largest Root:
Roy’s Largest Root是用于检验解释变量对因变量组合中最大单一效应的方法。其值大于等于0。较大的Roy’s Largest Root值表示解释变量对至少一个因变量的影响较大。通过比较Roy’s Largest Root值的观测值与在原假设下的期望值,我们可以得到一个p值,以判断解释变量对因变量组合中的最大单一效应是否显著。
解读结果:
对于这四种方法,我们需要关注它们对应的p值。如果p值小于预设的显著性水平(如0.05),则认为解释变量对因变量的整体影响或最大单一效应是显著的。在实际研究中,我们可以根据具体情况选择合适的方法。有时,研究者会选择多种方法进行检验以提高结果的稳定性。
Pillai’s Trace、Wilks’ Lambda、Hotelling’s Trace和Roy’s Largest Root都可以用于检验解释变量对多个因变量的整体影响。选择合适的方法取决于具体研究背景和数据特点。以下是一些建议:
数据分布和样本大小:对于小样本和数据分布偏离多元正态分布的情况,Pillai’s Trace和Wilks’ Lambda相对于Hotelling’s Trace和Roy’s Largest Root具有更好的稳健性。
统计功效:一般来说,Roy’s Largest Root在检验解释变量对因变量组合中最大单一效应时具有较高的统计功效,但可能较不稳健。相反,Pillai’s Trace和Wilks’ Lambda在检验解释变量对因变量的整体影响时具有较好的稳健性,但可能在某些情况下具有较低的统计功效。
结果一致性:在实际研究中,我们可以选择多种方法进行检验以提高结果的稳定性。如果这四种方法的结果相互一致,那么结论更具有可信度。
研究目的:根据研究目的,可以选择更关注整体效应的Pillai’s Trace和Wilks’ Lambda,或更关注最大单一效应的Hotelling’s Trace和Roy’s Largest Root。
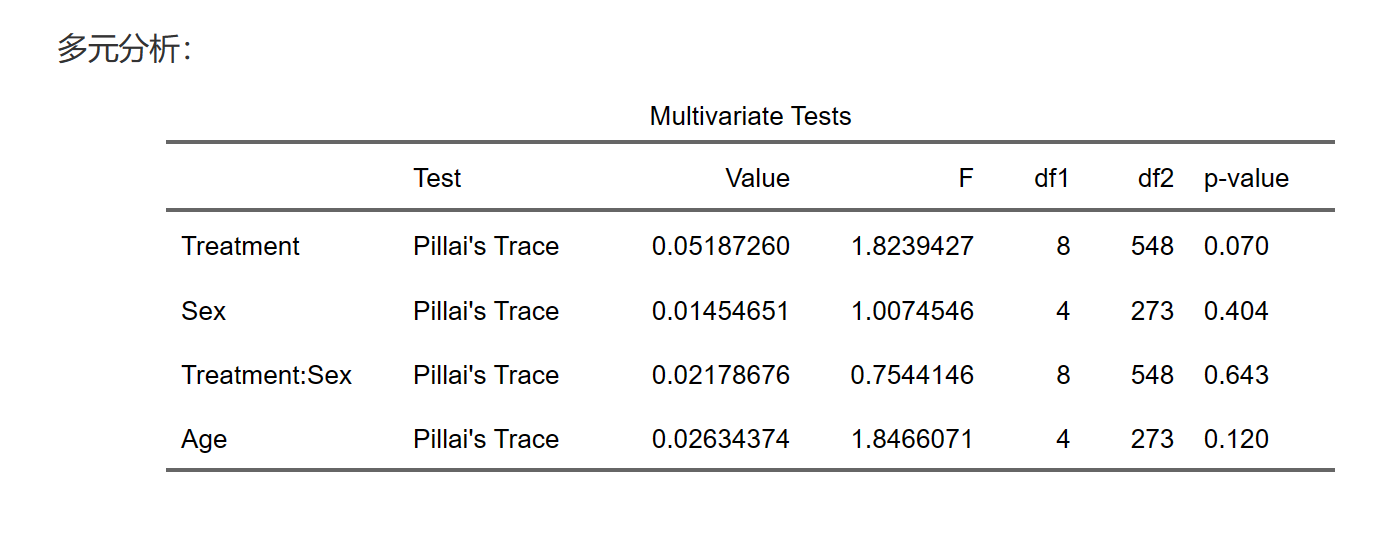
做完多元(协)方差分析之后,系统还会给出对每个因变量Y逐个进行传统方差分析的结果供参考。
9.16 重复测量方差分析(Repeated Measures ANOVA)
重复测量方差分析(Repeated Measures ANOVA)是一种统计方法,用于分析在相同实验单位上进行的多次观测之间的差异。该方法主要用于研究时间、条件或处理对实验单位的影响。重复测量方差分析可以考虑实验单位内的差异,并对此进行控制,以更准确地检测因素的作用。
使用场景:
研究某种干预或处理在不同时间点的效果。
比较多个实验条件下的实验单位表现。
研究时间与处理之间的交互作用。
例子1:临床上重复测量空腹血糖值,比较不同时间点血糖值的差异 在这个例子中,我们关注单一治疗组的患者在不同时间点的空腹血糖水平。例如,我们可以在开始治疗前、治疗后1个月、治疗后3个月和治疗后6个月测量空腹血糖值。通过使用重复测量方差分析,我们可以检测不同时间点空腹血糖值之间的差异,以便了解患者的血糖控制情况。
例子2:重复测量空腹血糖值,有三个治疗组,比较三组之间疗效的差异 在这个例子中,我们关注三个不同治疗组的患者在不同时间点的空腹血糖水平。例如,治疗组A接受药物1,治疗组B接受药物2,治疗组C接受药物3。我们可以在开始治疗前、治疗后1个月、治疗后3个月和治疗后6个月的时间点测量空腹血糖值。通过使用重复测量方差分析,我们可以检测三组之间的疗效差异(治疗组效应),不同时间点的血糖值差异(时间效应)以及时间与治疗组之间的交互作用。这有助于我们了解哪种药物对血糖控制的效果最好。
MSTATA 医学科研统计机器人提供了一站式的重复测量差分析步骤:
- 数据是否适合做重复测量方差分析:提供球形度检验、QQ图、方差齐性检验;
- 进行重复测量方差分析,设置重复测量单元和感兴趣的因子,可选交互作用或不选交互作用,设置要调整的协变量;
- 事后检验:对各水平亚组进行两两比较,可以调整多重比较的P值,可选Tukey法,Scheffe法,Bonferroni法和Holm法
- 计算效应量(effect size)
- 计算和比较各水平亚组的估计边际平均值(Estimated marginal means)和置信区间,生成统计表,绘制统计图
9.16.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
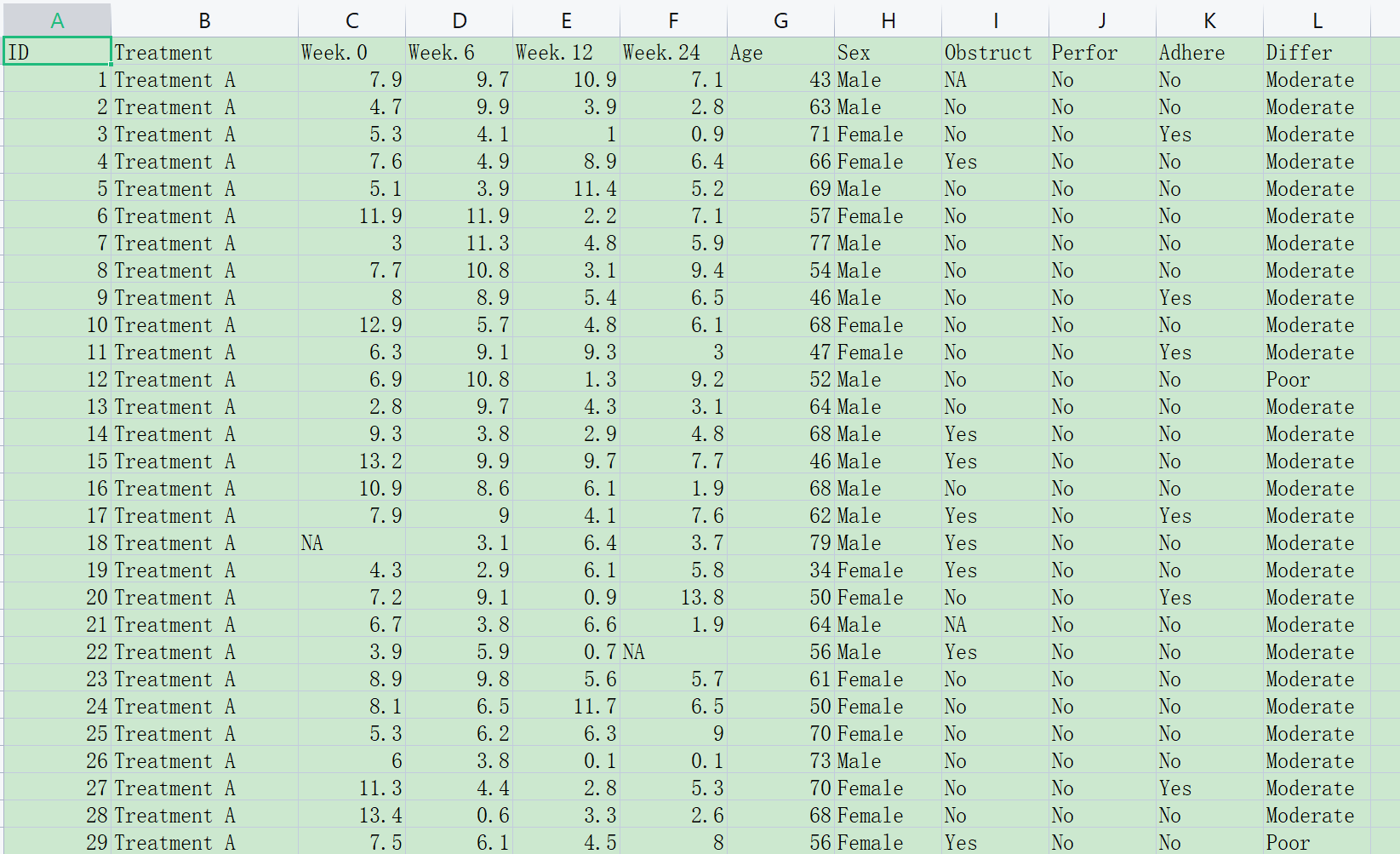
Week.0, Week.6, Week.12, Week.24 是一组重复测量的数据,为基线、6周、12周、24周的血糖值。
treatment是代表治疗组别的变量,这里有三个组Treatment A,Treatment B 和Control组。需要把变量属性设置成factor
sex是性别,也是我们感兴趣的组别变量, 要设为factor
Age是需要调整的协变量,为连续性变量,要设为numeric
9.16.3 设置重复测量单元
本例中0~24周的血糖测量,一共四个变量,值都是血糖水平,变量名用了Week.X 这样易于理解的时间标签。
把这几个变量点选中,即可组合成一个重复测量单元,注意点选的顺序需要按照事情发生的顺序来选,不可打乱。
给重复测量单元敲入一个易于展示的名称,这里我们命名为 Times,表示时间或次数。另外给指标也起一个名字,这里我们敲入”血糖值”,这两个名称都会在后面生成的统计图表中出现:

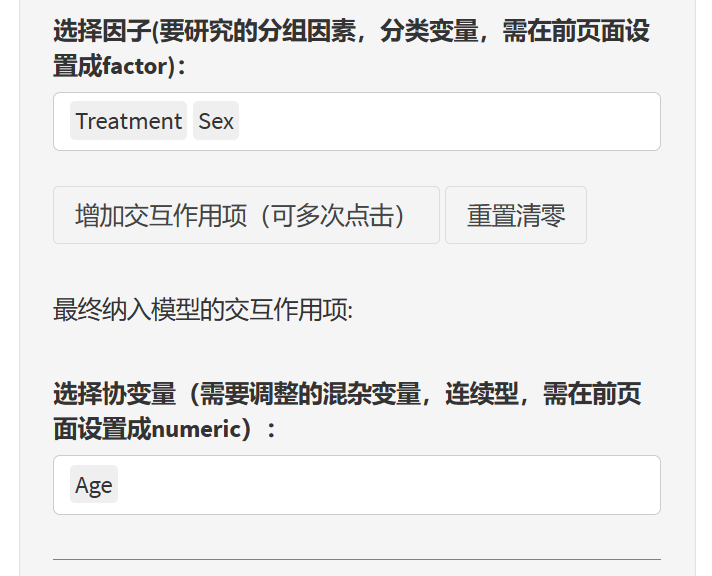
选择代表感兴趣的组别的因子,这里我们选treatment和sex,如果菜单里没有,则返回去把你想要的组别变量设置为factor
选择交互作用,每点击一次”增加交互作用项”按钮,就可以增加一个交互作用项菜单,在菜单里选两个以上的变量,就能将其合成交互作用项。这个例子中我们不设置交互作用。如果选错了要修改,可以点击”重置清零”按钮。
选择不感兴趣,用来做调整的协变量:这里age可能对结局有影响,但不是我们研究感兴趣的研究变量,因此勾选用来做协变量调整。
9.16.4 使用条件判断
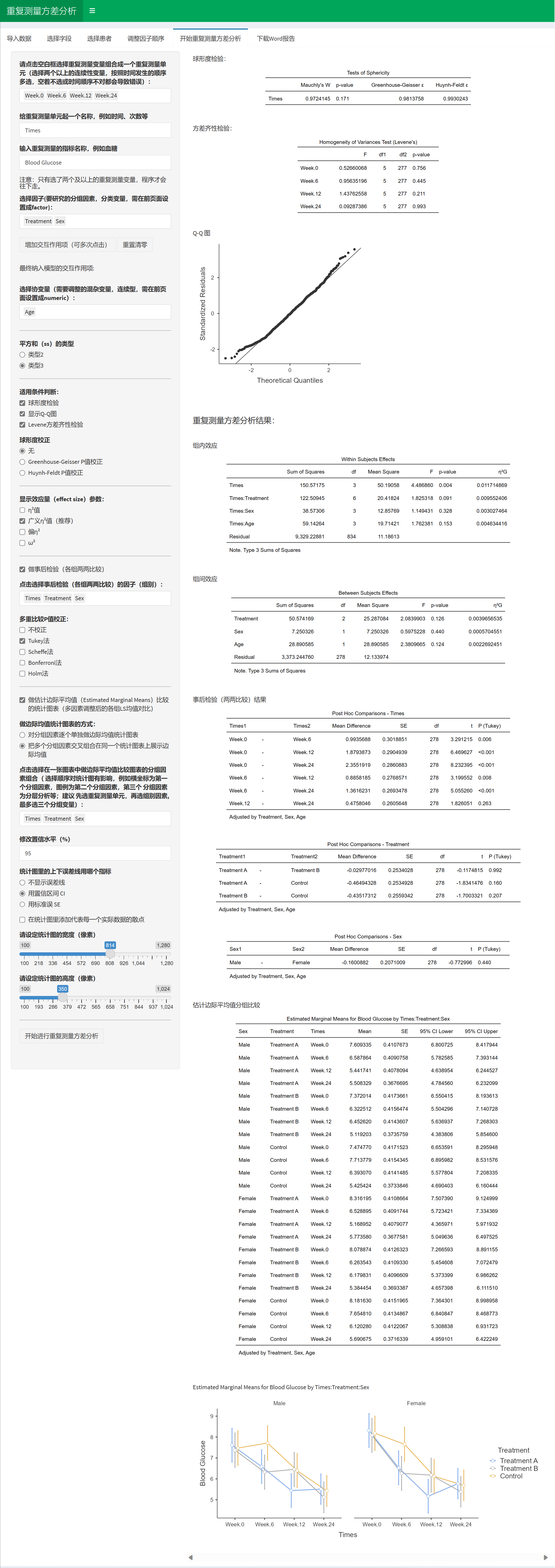
这里可以勾选球形度检验和方差齐性检验等。

球形度检验结果如下:

球形度检验(Tests of Sphericity)是在重复测量方差分析(Repeated Measures ANOVA)中用来检验数据是否满足球形假设(sphericity assumption)的方法。球形假设要求各水平之间的协方差相等,即各水平之间的方差和协方差矩阵是球形的。违反球形假设会导致重复测量方差分析的结果失真。
Mauchly’s W、Greenhouse-Geisser ε和Huynh-Feldt ε是常用的球形度检验方法:
Mauchly’s W:Mauchly’s W检验是最常用的球形度检验方法。它检验了协方差矩阵是否与恒等矩阵的充分接近。如果Mauchly’s W检验的p值小于预定的显著性水平(如0.05),则拒绝球形假设,认为数据违反了球形假设。
Greenhouse-Geisser ε:Greenhouse-Geisser修正是一种用于调整自由度的方法,以弥补违反球形假设所带来的影响。在使用Greenhouse-Geisser ε修正之后,可以通过比较调整后的F值与F分布的临界值来判断球形度。Greenhouse-Geisser ε的值介于0和1之间,当ε趋近于1时,说明球形假设趋于成立;反之,趋近于0则违反球形假设。
Huynh-Feldt ε:Huynh-Feldt修正是另一种调整自由度的方法。与Greenhouse-Geisser修正相比,Huynh-Feldt修正在估计自由度时相对较宽松,因此在实际应用中可能存在假阳性风险。Huynh-Feldt ε的值介于0和1之间,同样地,当ε趋近于1时,说明球形假设趋于成立;反之,趋近于0则违反球形假设。
在重复测量方差分析中,如果球形度检验表明数据违反了球形假设,那么通常需要采用Greenhouse-Geisser或Huynh-Feldt修正来调整自由度,以减小估计偏差,从而得到更准确的统计推断。选择哪种修正方法取决于实际情况,通常情况下,Greenhouse-Geisser修正较为保守,而Huynh-Feldt修正较为宽松。
9.16.5 重复测量方差分析的选项

这里可以选择平方和(ss)的类型,默认选类型3;

在重复测量方差分析中,效应量(effect size)是一个反映因素对因变量的影响程度的指标。常用的效应量指标有η²G(总组间效应量,Eta-squared generalized)、η²(组间效应量,Eta-squared)、η²p(偏组间效应量,Partial Eta-squared)和ω²(总组内效应量,Omega-squared)。
η²G(总组间效应量,Eta-squared generalized):η²G是一个描述整个模型中组间差异(即因素对因变量的影响)与总差异(因素效应和误差效应的总和)之间比例的指标。η²G的值介于0和1之间,值越大表示组间差异越明显,因素对因变量的影响越大。
η²(组间效应量,Eta-squared):η²是一个描述某个特定因素对因变量的影响程度的指标。它反映了该因素产生的差异与总差异之间的比例。与η²G类似,η²的值介于0和1之间,值越大表示该因素对因变量的影响越大。
η²p(偏组间效应量,Partial Eta-squared):η²p是一个描述某个特定因素对因变量的影响程度的指标,与η²类似,但是它考虑了其他因素的影响。它反映了该因素产生的差异与总差异(包括该因素和其他因素的影响)之间的比例。η²p的值介于0和1之间,值越大表示该因素对因变量的影响越大,同时考虑了其他因素的影响。
ω²(总组内效应量,Omega-squared):ω²是一个描述整个模型中组内差异(即误差效应)与总差异(因素效应和误差效应的总和)之间比例的指标。ω²的值介于0和1之间,值越大表示组内差异越明显,误差效应对因变量的影响越大。
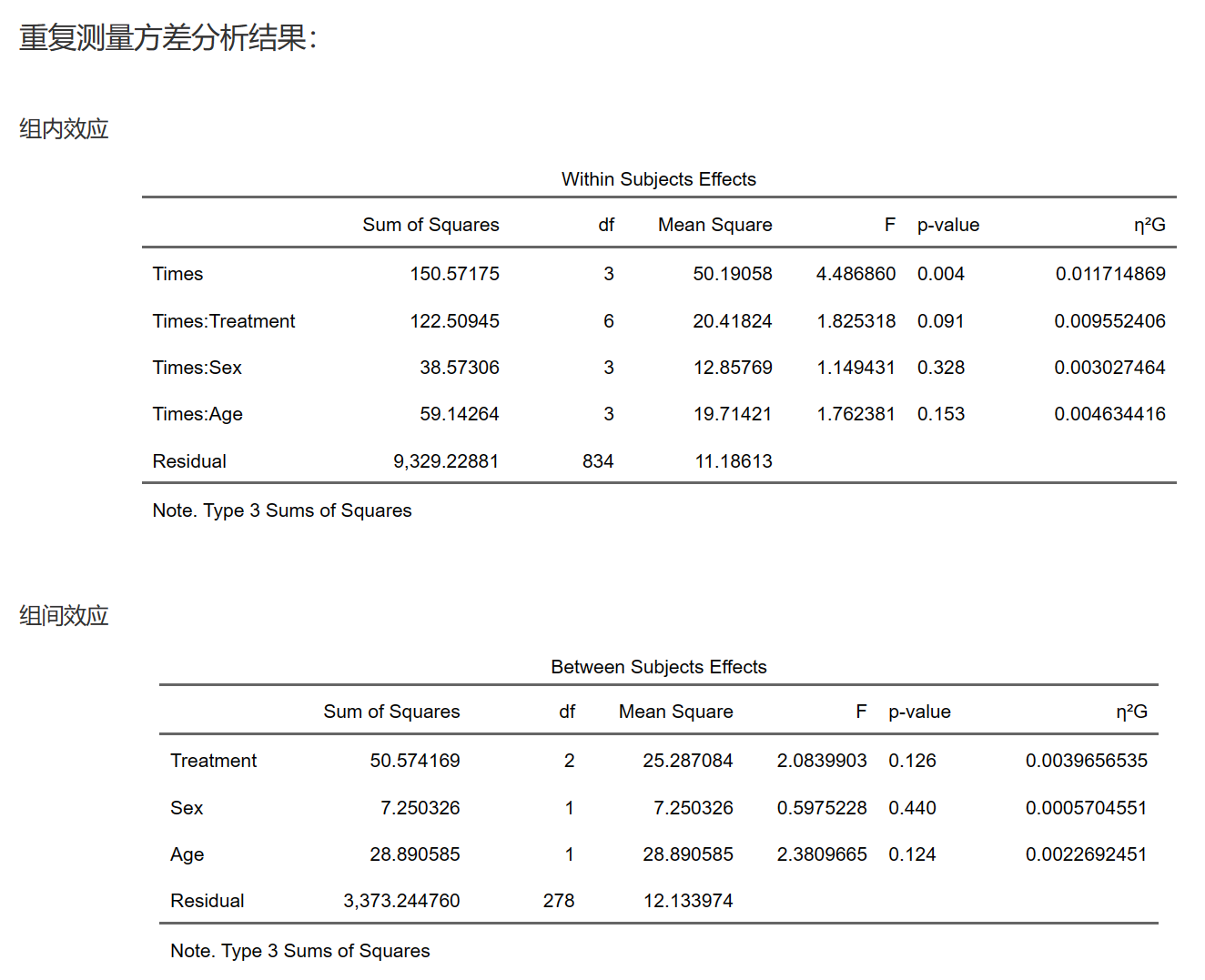
在重复测量方差分析中,Within Subjects Effects(组内效应)和Between Subjects Effects(组间效应)是两种不同类型的因素对因变量产生影响的方式。
Within Subjects Effects(组内效应):组内效应是指在同一实验单位内,在不同条件或时间点上的因变量值之间的差异。例如,在一个实验中,对同一组受试者在不同时间点进行测量,以研究某种干预措施的长期效果。
Between Subjects Effects(组间效应):组间效应是指在不同实验单位或组别之间的因变量值的差异。例如,在一个实验中,将受试者分为两个或多个组,每个组接受不同的干预措施,以研究不同干预措施之间的效果差异。
在重复测量方差分析的输出结果中,通常会看到以下统计量:
Sum of Squares(平方和):Sum of Squares是指因素效应、误差效应或总效应下,因变量值与其均值之差的平方和。它用于衡量因素、误差或总体中的变异性。
Mean Square(均方):Mean Square是平方和除以对应的自由度,即Sum of Squares的平均值。对于因素效应和误差效应,它们的均方分别用于计算F值。
F值(F统计量):F值是因素效应的均方与误差效应的均方之比。它用于检验因素对因变量的影响是否显著。F值越大,说明因素对因变量的影响越大,拒绝原假设(即认为因素对因变量有显著影响)的可能性越高。
P值(显著性水平):P值是在原假设成立的前提下,观察到当前或更极端F值的概率。通常情况下,如果P值小于预定的显著性水平(如0.05),则拒绝原假设,认为因素对因变量有显著影响。
在解释重复测量方差分析的结果时,需要分别关注Within Subjects Effects和Between Subjects Effects的F值和P值,以了解组内和组间因素对因变量的影响程度。同时,还需要关注效应量指标(如η²、η²p等),以了解因素对因变量的实际影响大小。
9.16.6 事后检验
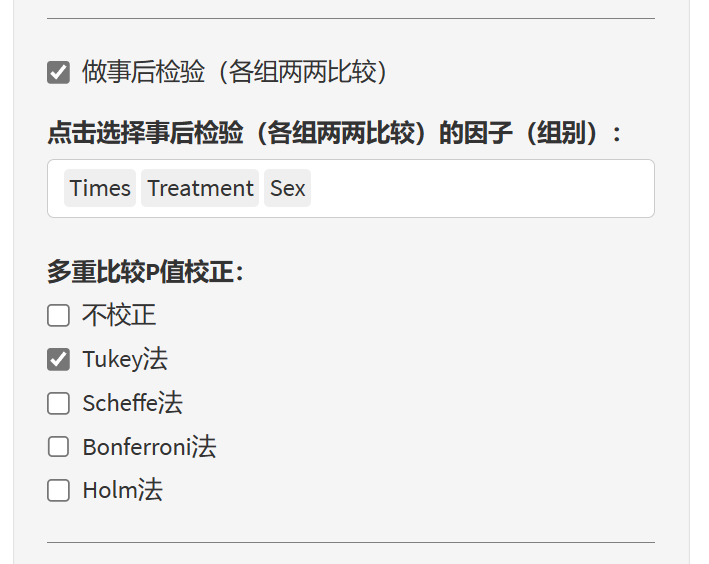
重复测量方差分析的事后检验(post hoc tests)用于在方差分析结果显著的情况下,进一步确定哪些组别之间存在显著差异。事后检验分为重复测量变量之间的事后检验和其他分组因素的事后检验。
重复测量变量之间的事后检验:这种事后检验主要关注不同时间点或条件下因变量之间的差异。当重复测量方差分析的Within Subjects Effects显著时,可以通过这类事后检验来确定具体哪些时间点或条件之间存在显著差异。常用的事后检验方法包括Tukey法、Scheffe法、Bonferroni法和Holm法。这些方法通过调整显著性水平或P值,来控制多重比较带来的假阳性风险。
其他分组因素的事后检验:这种事后检验主要关注不同组别之间因变量的差异。当重复测量方差分析的Between Subjects Effects显著时,可以通过这类事后检验来确定具体哪些组别之间存在显著差异。同样可以采用Tukey法、Scheffe法、Bonferroni法和Holm法进行事后检验。
以下简要介绍这四种方法:
Tukey法(Tukey’s Honestly Significant Difference, Tukey’s HSD):Tukey法主要用于多组比较,可以在保证整体显著性水平的前提下,确定哪些组别之间存在显著差异。适用于组间样本量相等的情况。
Scheffe法(Scheffé’s method):Scheffe法适用于各种自由度的比较,包括两两比较和多重比较。它较为保守,适用于组间样本量不等的情况。
Bonferroni法(Bonferroni correction):Bonferroni法通过将原显著性水平除以比较次数来调整显著性水平,从而控制整体显著性水平。它是一种保守的方法,但在多重比较较多时可能过于保守。
Holm法(Holm-Bonferroni method):Holm法是对Bonferroni法的改进,它通过对P值进行排序和按顺序进行调整,以减轻Bonferroni法在多重比较较多时过于保守的问题。
在选择事后检验方法时,研究者需要权衡实际情况和对误差控制的需求,以得到准确的统计
这里我们选了不同时间点之间的比较,不同治疗组之间的比较,和不同性别之间的比较。
如果需要进一步交叉比较,例如每个治疗组中不同时间点比较,或者每个时间点中不同治疗组的比较,则应该在事后检验的菜单中选择中交互作用Times:Treatment进行事后检验。
9.16.7 估计边际平均值
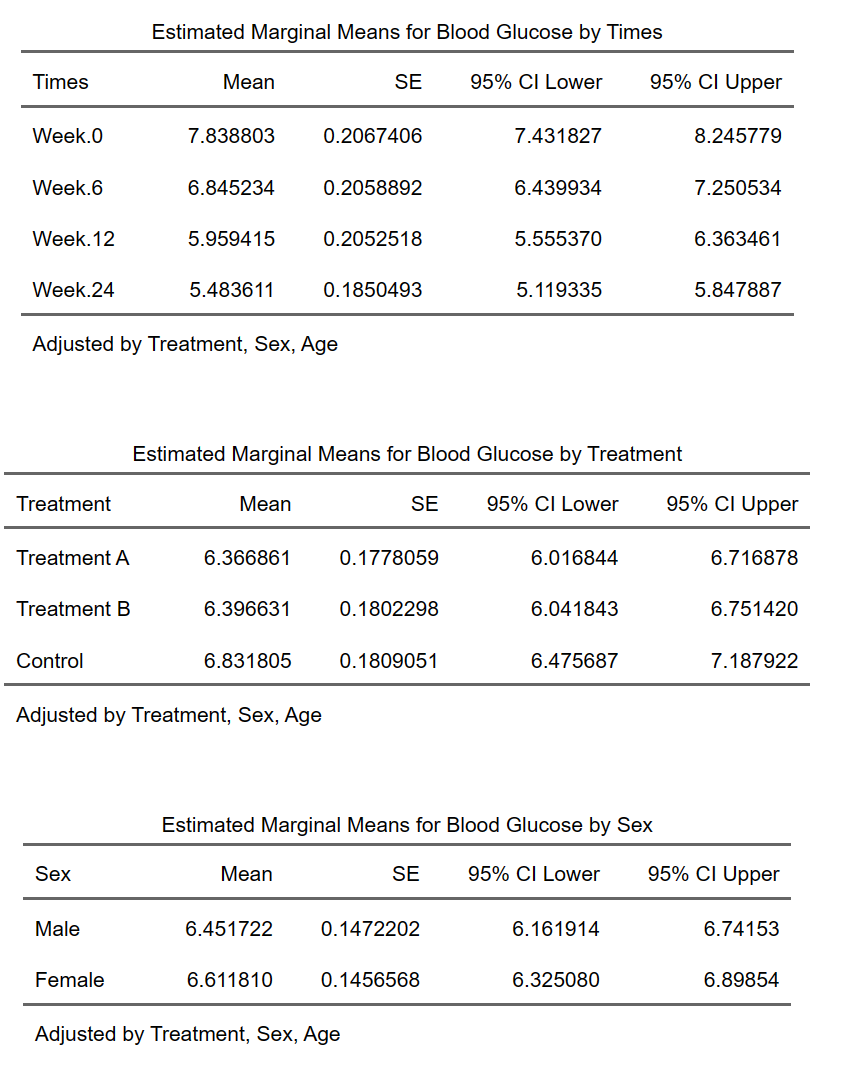
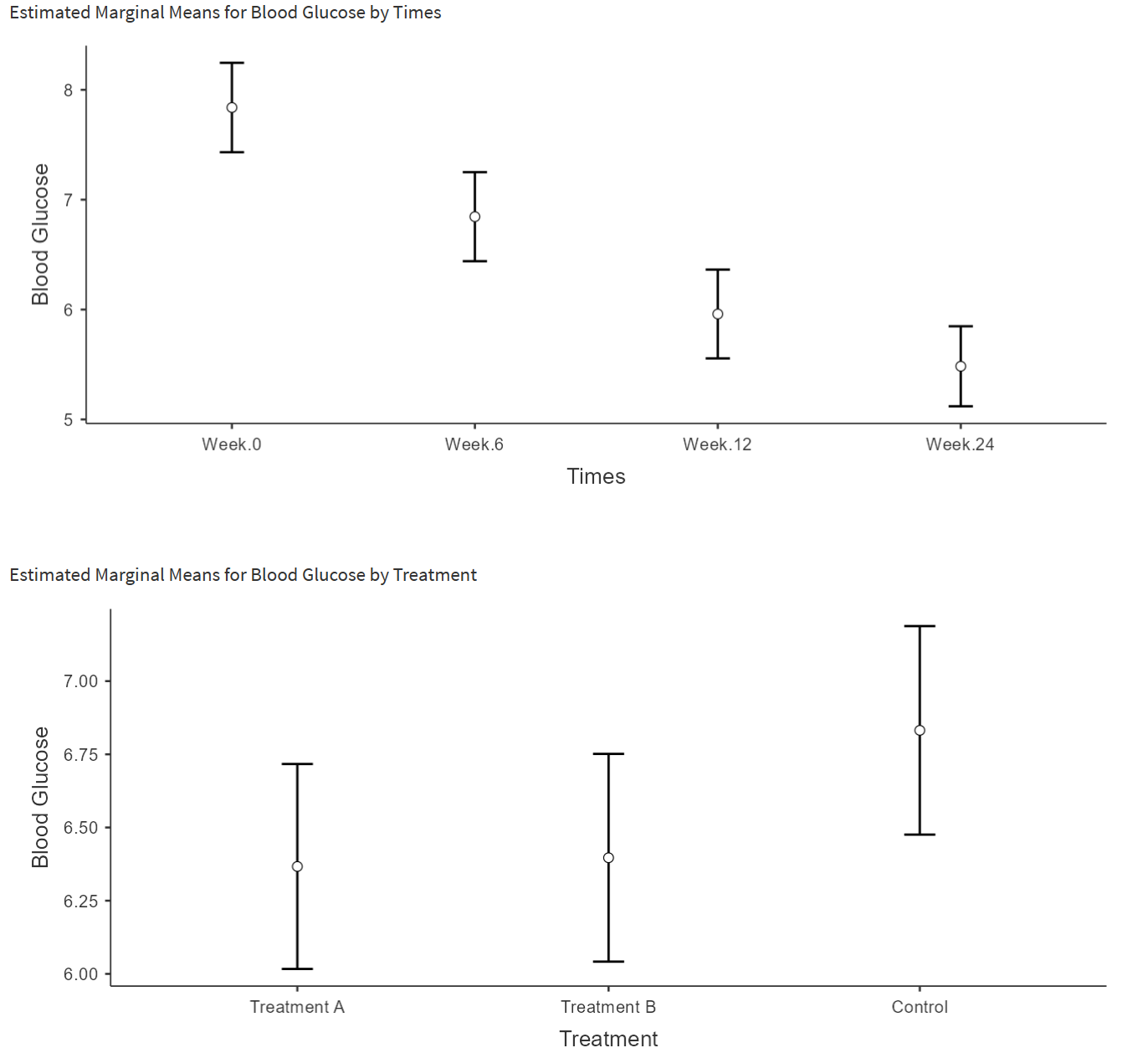
重复测量方差分析中的Estimated Marginal Means(估计边际均值)是一种描述性统计量,用于表示在考虑所有其他因素的影响下,某一特定因素水平的平均因变量值。估计边际均值是通过将模型中的其他因素固定在它们的平均水平上,并计算给定因素水平的平均因变量值来获得的。
在重复测量方差分析中,可以对重复测量的时间点和其他分组因素分别单独进行估计边际均值的展示,也可以将这几个因素交互在同一个统计表中。这有助于更好地理解和展示因素水平对因变量的影响。
单独对时间点进行估计边际均值的展示:这种方法将展示不同时间点上因变量的估计边际均值,以及它们之间的差异。这有助于了解在不同时间点上因变量值的变化趋势。
单独对其他分组因素进行估计边际均值的展示:这种方法将展示不同分组因素水平上因变量的估计边际均值,以及它们之间的差异。这有助于了解不同分组因素水平对因变量的影响程度。
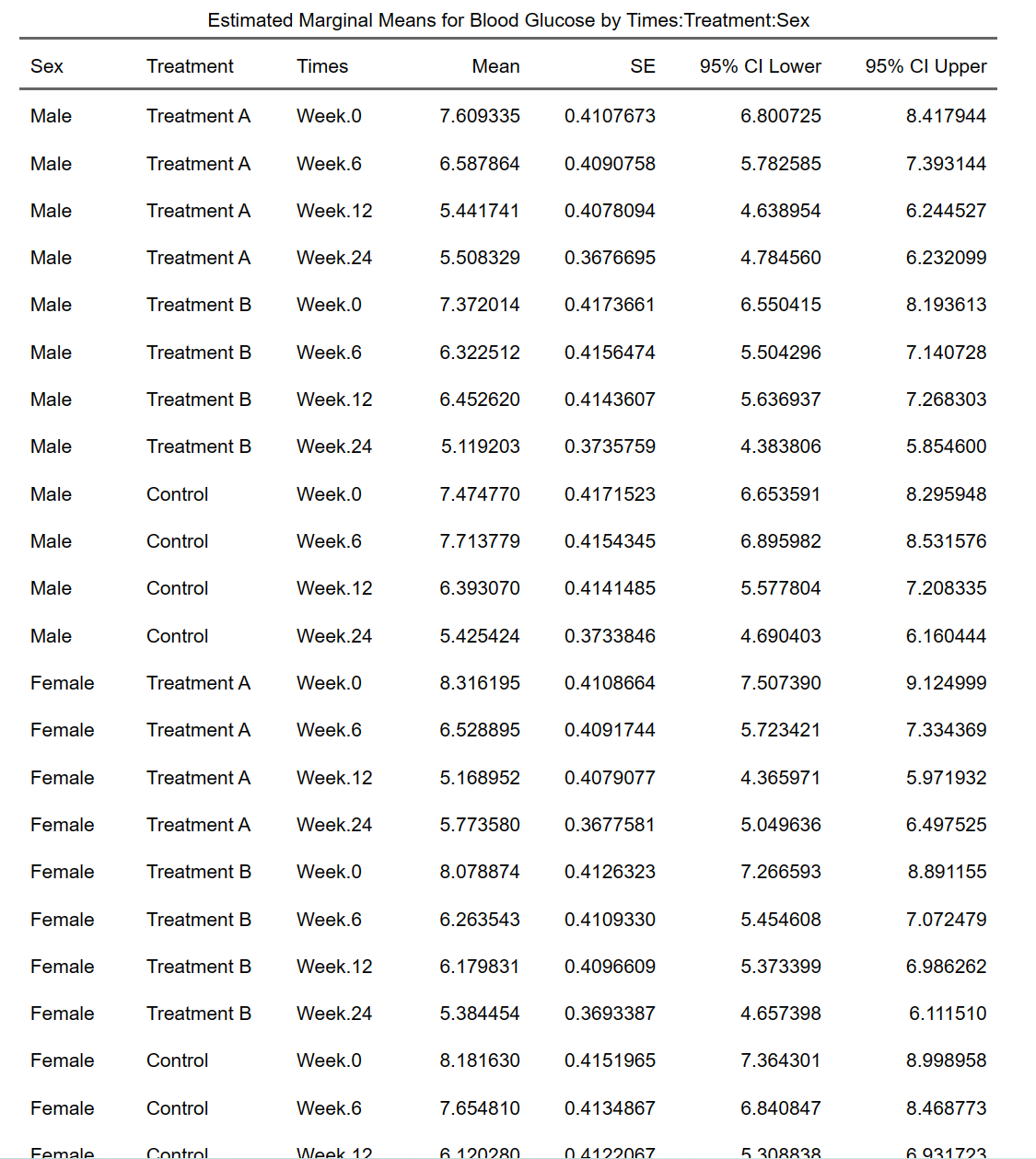
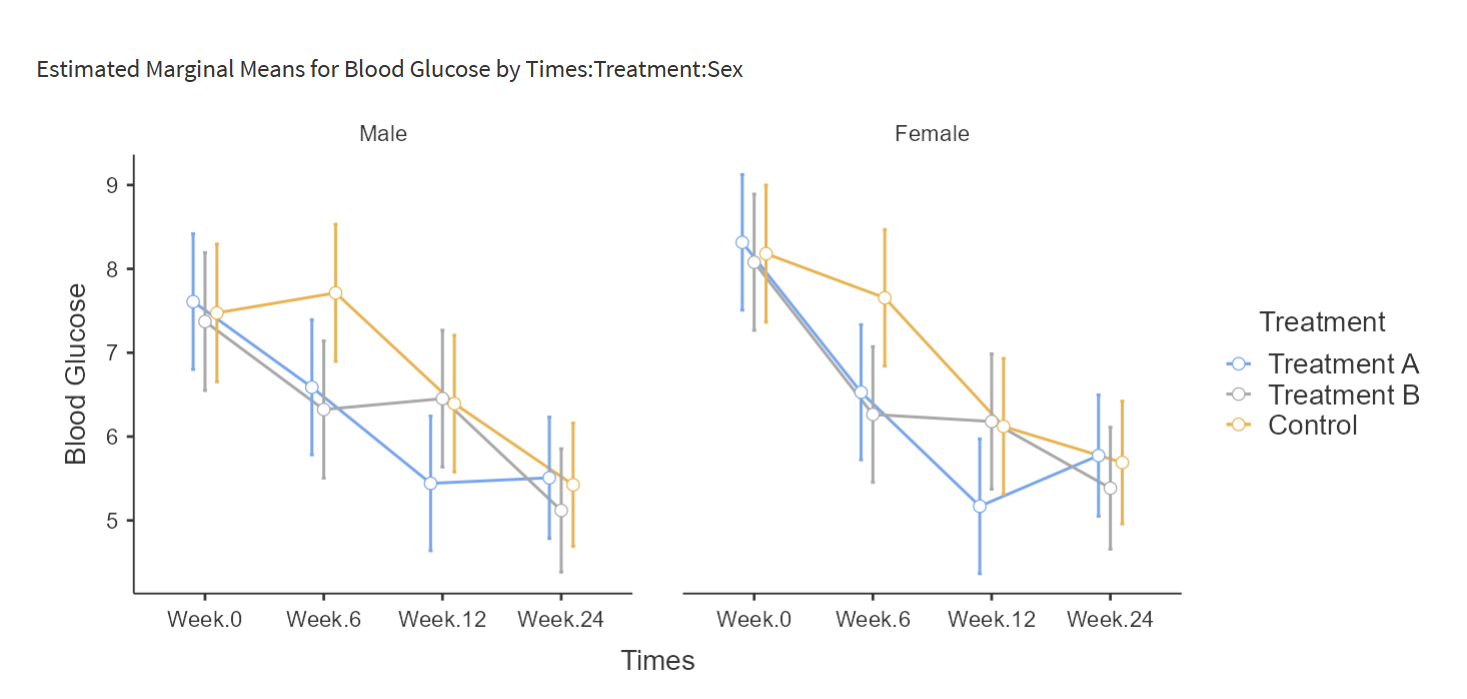
将重复测量时间点和其他分组因素交互在同一个统计表中:这种方法将展示不同时间点和分组因素水平组合下因变量的估计边际均值,以及它们之间的差异。这有助于了解时间点和分组因素之间的交互作用对因变量的影响。
在绘制统计图时,也可以采用类似的方式来展示估计边际均值。例如,可以绘制线图来展示不同时间点上的估计边际均值,或者绘制条形图来展示不同分组因素水平上的估计边际均值。对于交互作用的展示,可以在同一图中绘制多条曲线或多组柱状图,以展示不同时间点和分组因素水平组合下的估计边际均值。这将有助于更直观地了解因素水平对因变量的影响及其交互作用。
分别对各分组因素进行估计边际均值的展示:
把各因素交叉组合在同一张统计图表中:
9.17 一般线性回归
线性回归是一种统计学方法,用于研究两个或多个变量之间的关系,通常用于预测一个因变量(响应变量)基于一个或多个自变量(预测变量)。线性回归的关键在于拟合出一个线性方程,最大程度地解释自变量与因变量之间的关系。在医学研究领域,线性回归常被用于分析连续型数据,例如研究血压与年龄、性别、体重指数(BMI)等相关因素之间的关系。
以下是一个医学研究中应用线性回归的例子:
假设我们要研究收缩压(因变量)与年龄、性别、体重指数(BMI)等危险因素(自变量)之间的关系。在这个例子中,我们可以运用线性回归模型来预测收缩压的变化,进而分析这些危险因素与收缩压之间是否存在显著关系。
MSTATA统计软件中的线性回归模块提供了线性回归的所有相关功能,包括:
- 设置自变量:可根据研究目的设置一个或多个自变量。
- 支持交互作用项:可以分析自变量间的交互作用对因变量的影响。
- 设置分类自变量的参照水平:方便进行多水平分类自变量的比较。
- 适用条件判断:
做自相关分析:检查自变量间是否存在自相关,以确保模型稳定性。
做多重共线性分析:检查自变量间是否存在多重共线性,以确保模型稳定性。
做正态性检验:检验因变量和残差的正态性假设。
做残差Q-Q图、做残差图、Cook’s 距离:评估模型假设的满足程度和异常值的存在。
- 显示模型系数的置信区间、显示标准化系数、显示标准化系数的置信区间:方便对各自变量的影响力进行评估。
- Omnibus方差检验:检验模型整体的显著性。
- 模型拟合优度评价:包括复相关系数R、决定系数R²、校正R²、AIC、BIC、均方根误差(RMSE)以及整体模型F检验。
- 做估计边际平均值:包括生成估计边际平均值(统计图和表)。

9.17.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
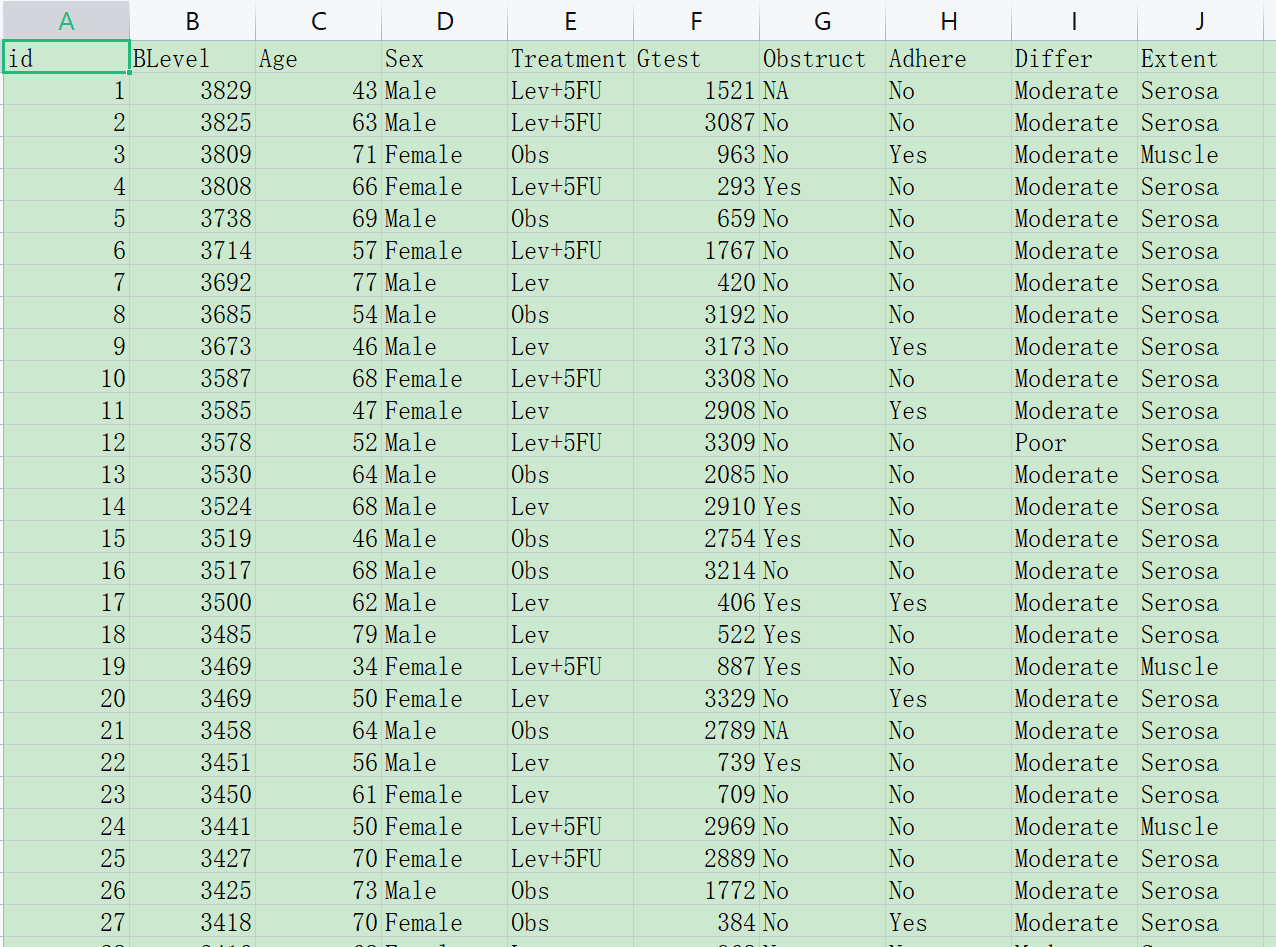
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
代表结局的应变量:例如上图中的BLevel,是一项血液学指标。
解释变量(自变量):例如上图中的age、sex等等一系列指标。
解释(自)变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄\[岁\]、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 Age和Gtest是连续性变量(numeric), 其他的是分类变量(factor)。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
9.17.3 线性回归分析
下一步就是回归分析啦:
选择结局(应)变量 在”请选择结局(应)变量”下拉框中,选择一个连续性变量作为因变量。如果您需要的变量不在列表中,请返回设置将其更改为numeric类型。
选择自变量/解释变量 在”请点击空白框选择自变量/解释变量”下拉框中,选择一个或多个变量作为自变量。如果您需要的字段不在列表中,可能是因为连续性变量被设置成了分类变量,请返回修改。
添加交互作用项 点击”增加交互作用项(可多次点击)“按钮,然后在弹出的选择框中选择至少两个变量以创建交互作用项。您可以多次点击以添加更多交互作用项。
重置清零 如需重置所有已添加的交互作用项,点击”重置清零”按钮。
选择参照组 对于每个非数值因子,从下拉框中选择一个参照组。
适用条件判断 在此部分,您可以选择进行以下分析:
自相关分析(Durbin-Watson 检验): 在线性回归中,自相关分析主要用于检测残差(观测值与预测值之间的差异)之间的相关性。Durbin-Watson 检验是一种常用的方法,检验统计量的值在 0 到 4 之间,接近 2 表示不存在自相关。如果存在显著的自相关,可能需要考虑更复杂的模型,如时间序列模型。
多重共线性分析: 多重共线性是指线性回归模型中,两个或多个自变量之间存在较强的相关性。多重共线性可能导致模型系数估计不稳定,降低解释性。检测方法有方差膨胀因子(VIF)等。VIF 值大于 10 通常被认为表明存在多重共线性。解决方法包括删除相关变量、使用主成分分析等。
正态性检验: 线性回归模型中,正态性检验主要用于检验残差的正态分布假设。常用方法有 Shapiro-Wilk 检验等。若残差不符合正态分布,可能需要考虑变量转换或非线性模型。
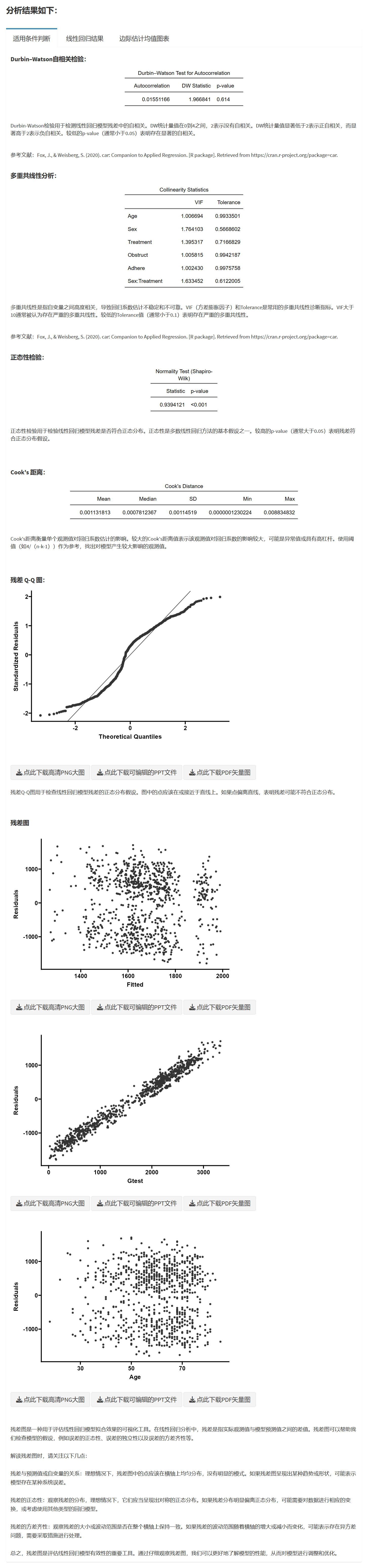
残差 Q-Q 图: Q-Q 图是一种图形化方法,用于检验残差的正态分布假设。理想情况下,Q-Q 图上的点应在一条直线上。如果点明显偏离直线,表明残差可能不符合正态分布。
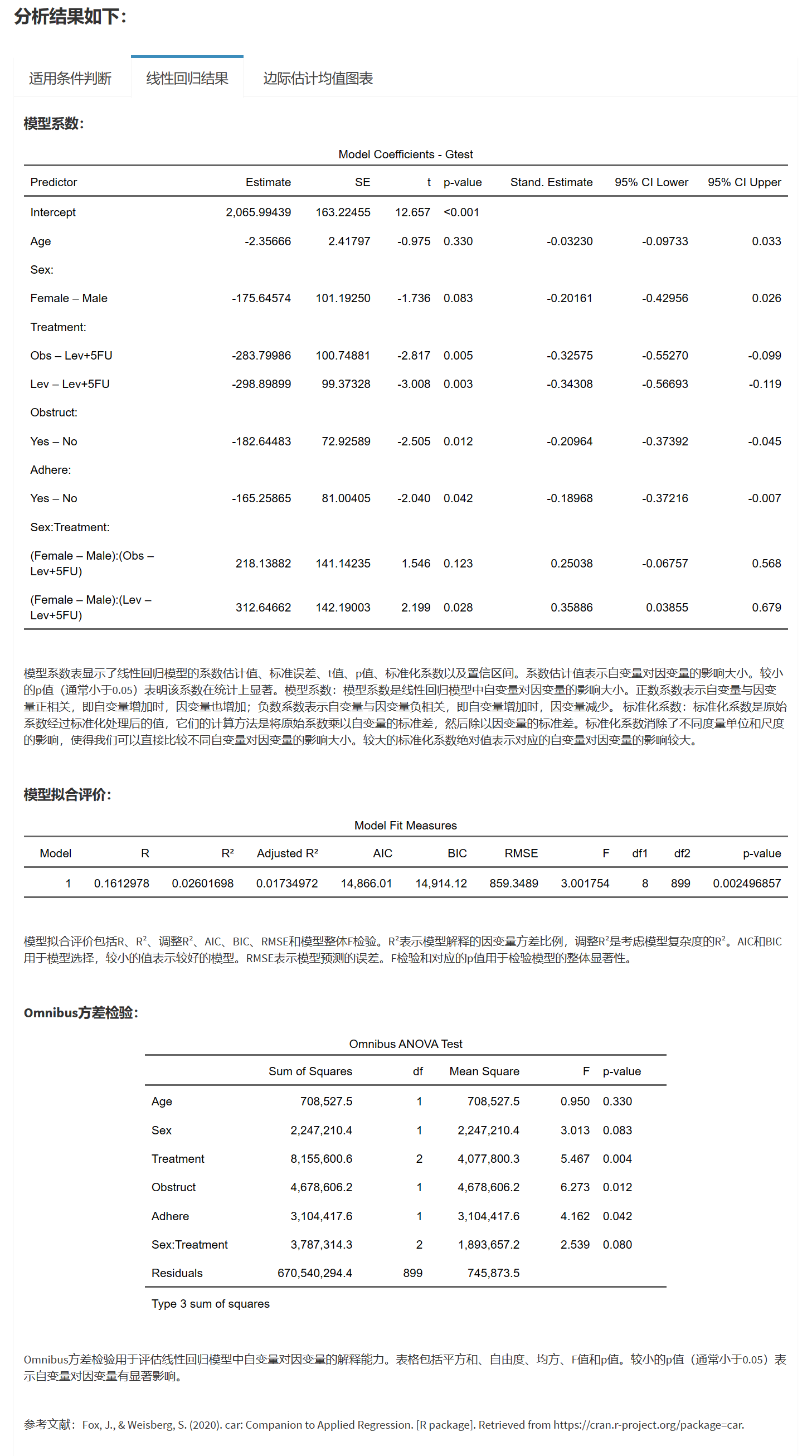
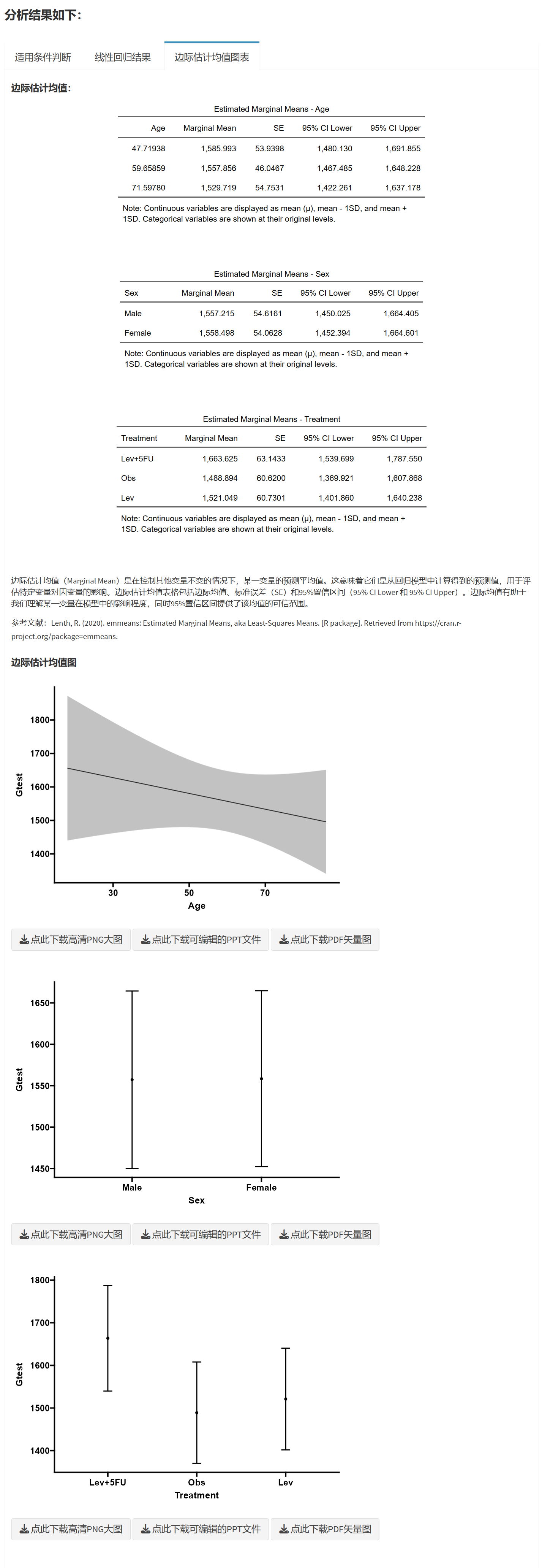
残差图: 残差图用于检查线性回归模型的拟合情况。通常横坐标为预测值,纵坐标为残差。理想情况下,残差应在 0 附近随机分布,无明显模式。如果残差图呈现出特定模式,可能需要考虑非线性模型。
Cook’s 距离: Cook’s 距离是一种衡量观测值对模型参数估计影响程度的统计量。较大的 Cook’s 距离值表明某个观测值对模型拟合产生较大影响,可能是离群值或高杠杆点。通常可设定阈值,如 4/n(n 为观测数),若某观测值的 Cook’s 距离大于阈值,则需要进一步审查
模型拟合优度评价 在此部分,您可以选择显示以下模型拟合优度指标:
复相关系数R
决定系数R²
校正R²
AIC
BIC
均方根误差(RMSE)
整体模型F检验
显示模型系数 您可以选择显示模型系数的置信区间和标准化系数。如果需要,还可以显示标准化系数的置信区间。
Omnibus 检验 您可以选择进行方差分析。
边际估计均值统计图表 您可以选择对每个因素逐个单独做边际估计均值统计图表,或者把多个因素交叉组合在同一个统计图表上展示边际估计均值。此外,您还可以设置显示置信区间,修改置信水平,以及设定统计图的宽度和高度(像素)。
开始进行线性回归 设置完成后,点击”开始进行线性回归”按钮,开始分析
9.18 二分类 Logistic 回归(Y 为二分类变量)
Logistic回归是一种广义线性模型,适用于处理具有二分类结果的因变量。Logistic回归的特点是使用logit函数将线性预测子与因变量之间的关系建立起来,从而可以预测事件发生的概率。在医学研究中,Logistic回归常用于分析疾病发生与危险因素之间的关系。
以下是一个医学研究中应用Logistic回归的例子:
假设我们要研究糖尿病(因变量)与年龄、性别、体重指数(BMI)等危险因素(自变量)之间的关系。在这个例子中,我们可以运用Logistic回归模型来预测糖尿病发生的概率,进而分析这些危险因素与糖尿病之间是否存在显著关系。
MSTATA统计软件中的Logistic回归模块提供了Logistic回归的所有相关功能,可谓集大成者,包括:
设置自变量:可根据研究目的设置一个或多个自变量。
支持交互作用项:可以分析自变量间的交互作用对因变量的影响。
设置分类自变量的参照水平:方便进行多水平分类自变量的比较。
适用条件判断(多重共线性分析):检查自变量间是否存在多重共线性,以确保模型稳定性。
展示回归系数:输出每个自变量对应的回归系数。
展示OR值和可信区间:方便对各自变量的影响力进行评估。
模型拟合评价:包括Deviance、AIC、BIC、McFadden’s R²、Cox & Snell’s R²和Nagelkerke’s R²。
做Omnibus似然比检验:检验模型整体的显著性。
Estimated Marginal Means分析:包括生成估计边际平均值(概率图)。
诊断预测和ROC曲线:评估模型的诊断能力。
ROC曲线评估:计算AUC值及灵敏度特异度等,评估模型的区分能力。
生成cut-off图:根据截断点,进行分类预测。
生成分类表(混淆矩阵):用于评估模型的预测准确性。
导出Word格式的统计报告:方便进一步编辑和整理。
9.18.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
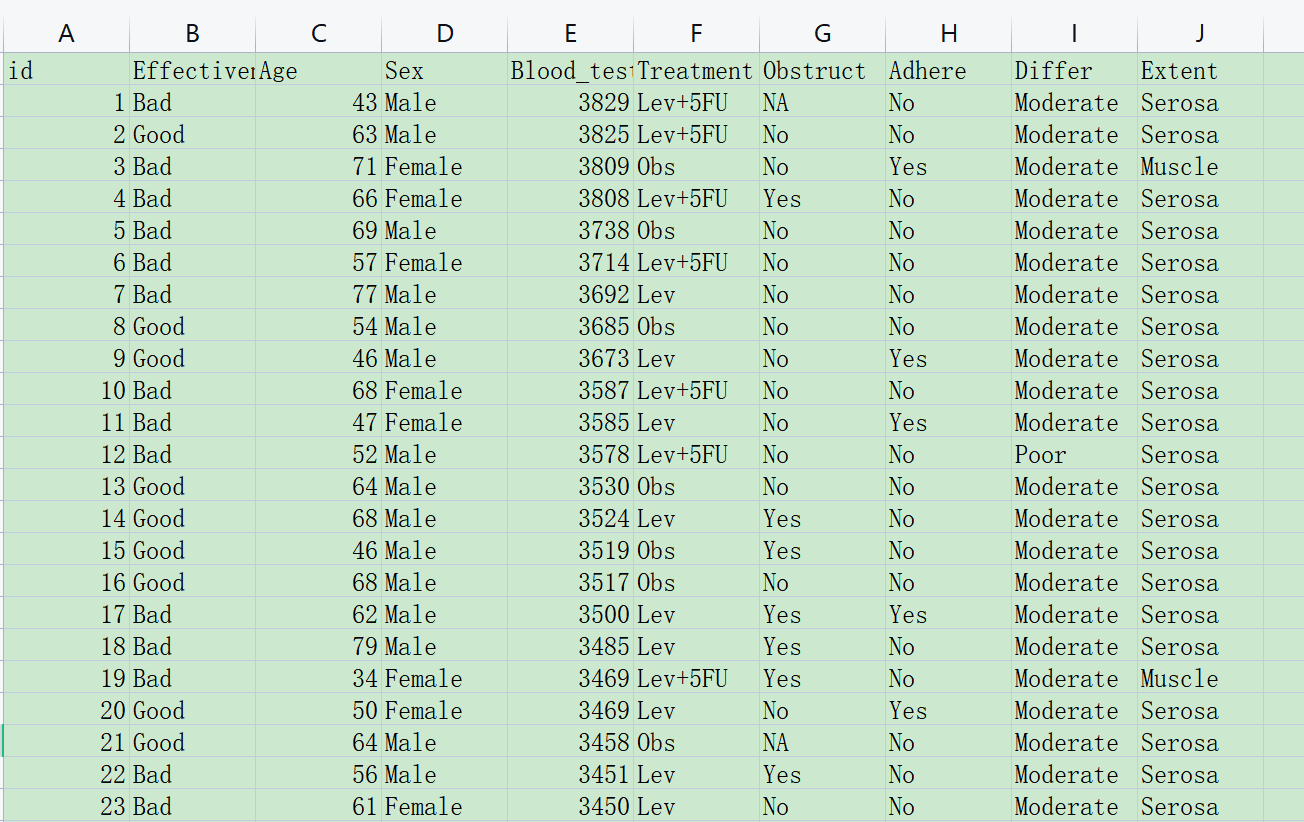
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
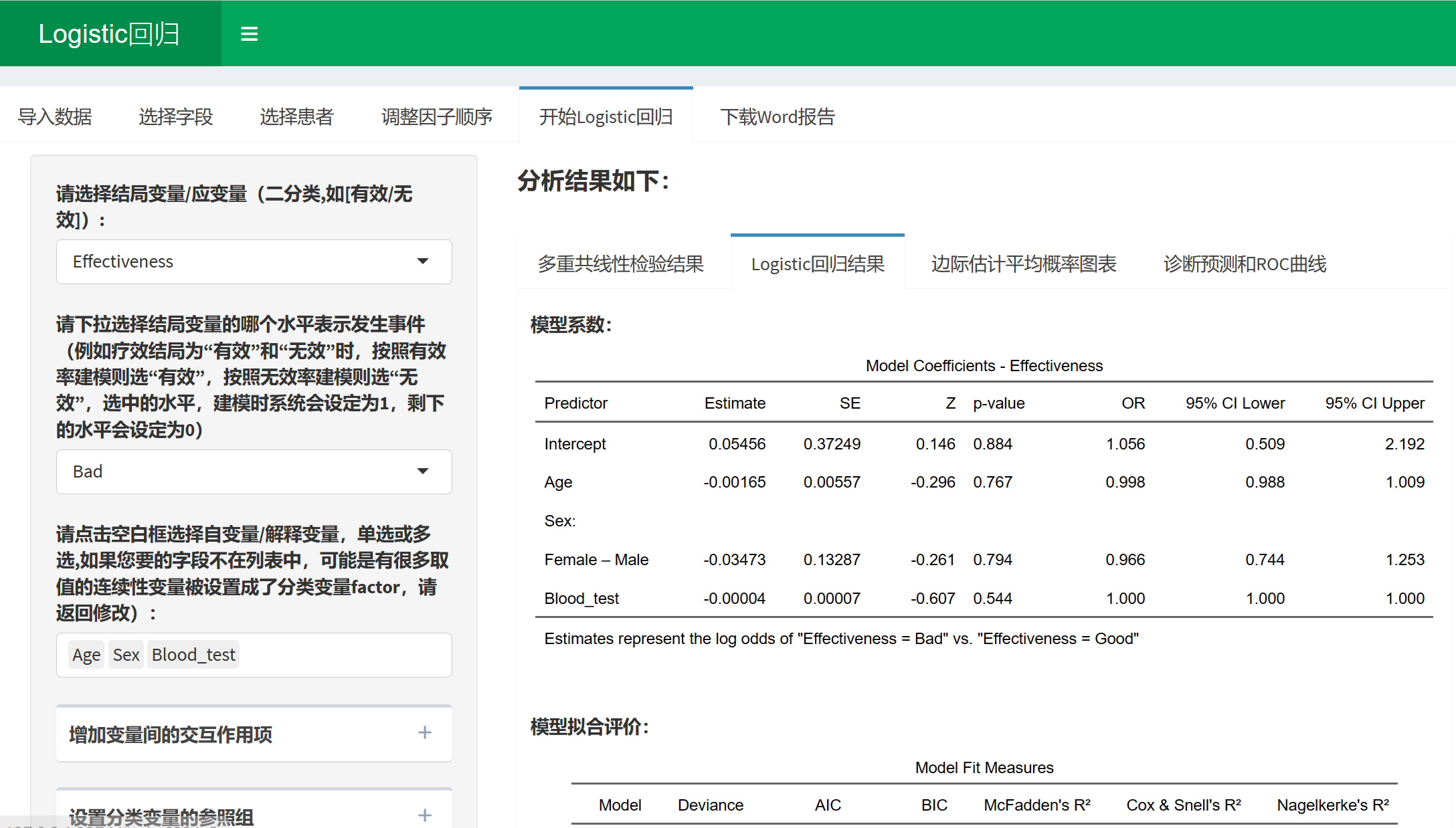
代表结局的应变量:例如上图中的Effectiveness,有疗效Good、Bad两种情况
解释变量(自变量):例如上图中的age、sex等等一系列指标。
解释(自)变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄\[岁\]、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 Age和Blood_test是连续性变量(numeric), 其他的是分类变量(factor)。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
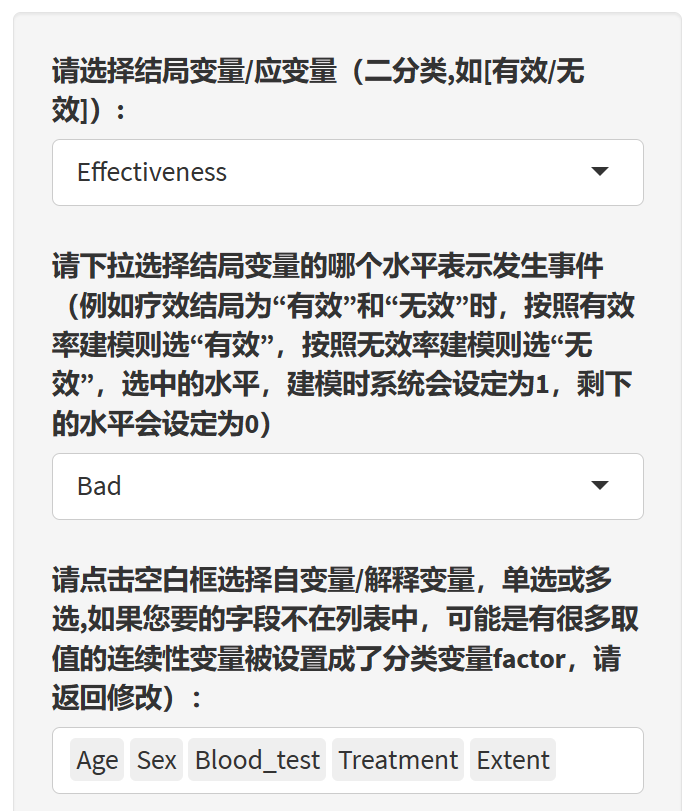
9.18.4 选择解释变量(自变量)
根据提示选择自变量。这里要注意的是,如果上传的数据Excel文件里把连续性变量设置成了字符型,如年龄设置成了字符型,需要在前面”选择字段”功能里改回成numeric,如果按照分类变量放进影响因素分析。同理,如果把ID号也作为分类变量放进影响因素,也会出问题。
另外,在分类变量里,有些亚组人数很少,最好把它和其他亚组合并之后再传上来分析,亚组人数太少容易让可信区间特别宽,影响排版。当然,后续我们也会增加一个合并亚组的小工具。
9.18.5 选择交互作用
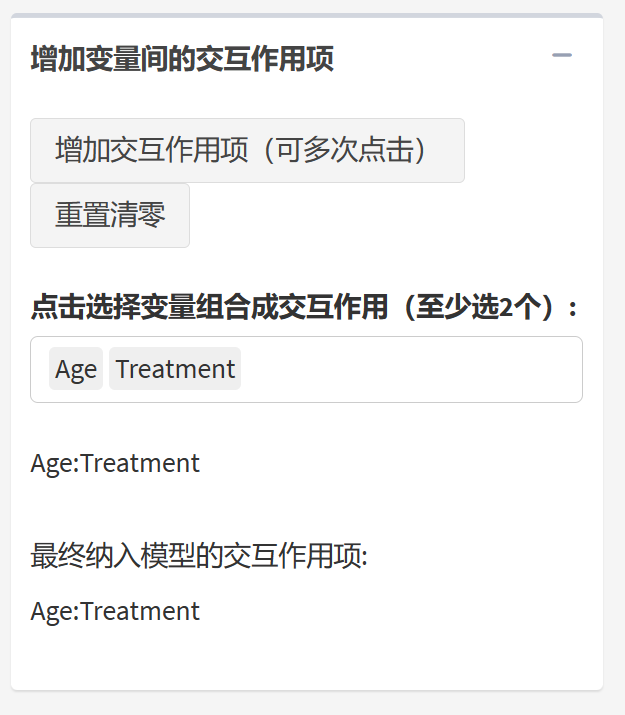
点开交互作用选项,点击增加交互作用项按钮,选定两个及以上变量即可生成交互作用项,如果要增加多个交互作用项,重复点击”增加交互作用项”按钮即可;如果选错了,点击重置清零即可。
9.18.7 多重共线性分析

多重共线性是指自变量之间存在较高的相关性,可能导致回归系数估计不稳定,影响模型解释和预测能力。在Logistic回归中,多重共线性分析的目的是检查模型中自变量间是否存在较强的线性关系,以便在建模过程中采取相应措施。
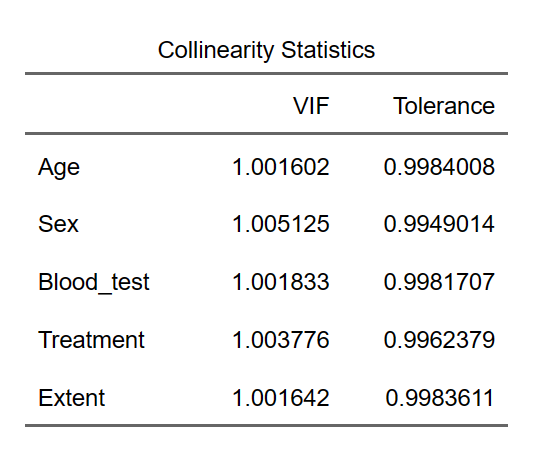
多重共线性的判断通常基于方差膨胀因子(Variance Inflation Factor, VIF)和容忍度(Tolerance)两个指标。
- 方差膨胀因子(VIF):VIF是一个衡量多重共线性程度的指标,可以反映自变量的方差与无共线性情况下的方差之间的比值。VIF值越大,表示该自变量与其他自变量之间的共线性越强。通常,VIF值大于10被认为存在较强的多重共线性。
计算公式:VIF = 1 / (1 - R²)
其中,R²是该自变量作为因变量,其他自变量作为解释变量时,线性回归模型的解释力。
- 容忍度(Tolerance):容忍度是VIF的倒数,用于衡量一个自变量与其他自变量之间的独立性。容忍度值越小,表示该自变量与其他自变量之间的共线性越强。通常,容忍度值小于0.1被认为存在较强的多重共线性。
计算公式:Tolerance = 1 - R²
在实际应用中,可以通过计算每个自变量的VIF和容忍度来判断多重共线性的程度。如果发现存在较强的多重共线性,可以采取以下措施:
增加样本量:有时候多重共线性是由于样本量不足导致的,增加样本量可能有助于降低多重共线性。
删除某些自变量:如果某些自变量之间存在强相关性,可以考虑删除其中之一,以降低多重共线性。
组合自变量:对于高度相关的自变量,可以考虑将它们组合成一个新的自变量。
引入Lasso或者岭回归等方法:这些方法可以在一定程度上解决多重共线性问题。
总之,在进行Logistic回归分析时,应关注多重共线性的问题,通过VIF和容忍度等指标判断自变量间的相关性,并采取相应措施以确保模型的稳定性和解释力。
可以用本站另外一个APP”从单因素到多因素分析中自动变量筛选”功能来筛选变量,APP位于www.mstata.com , “以临床研究类型分类” - “影响因素分析” 菜单
多重共线性分析结果:
9.18.8 Logistic回归结果展示选项
选择结果展示的表格外观:
可以选择是否显示回归系数的置信区间、是否显示OR值,是否显示OR值的置信区间,以及是否做似然比检验。
回归分析结果如下:
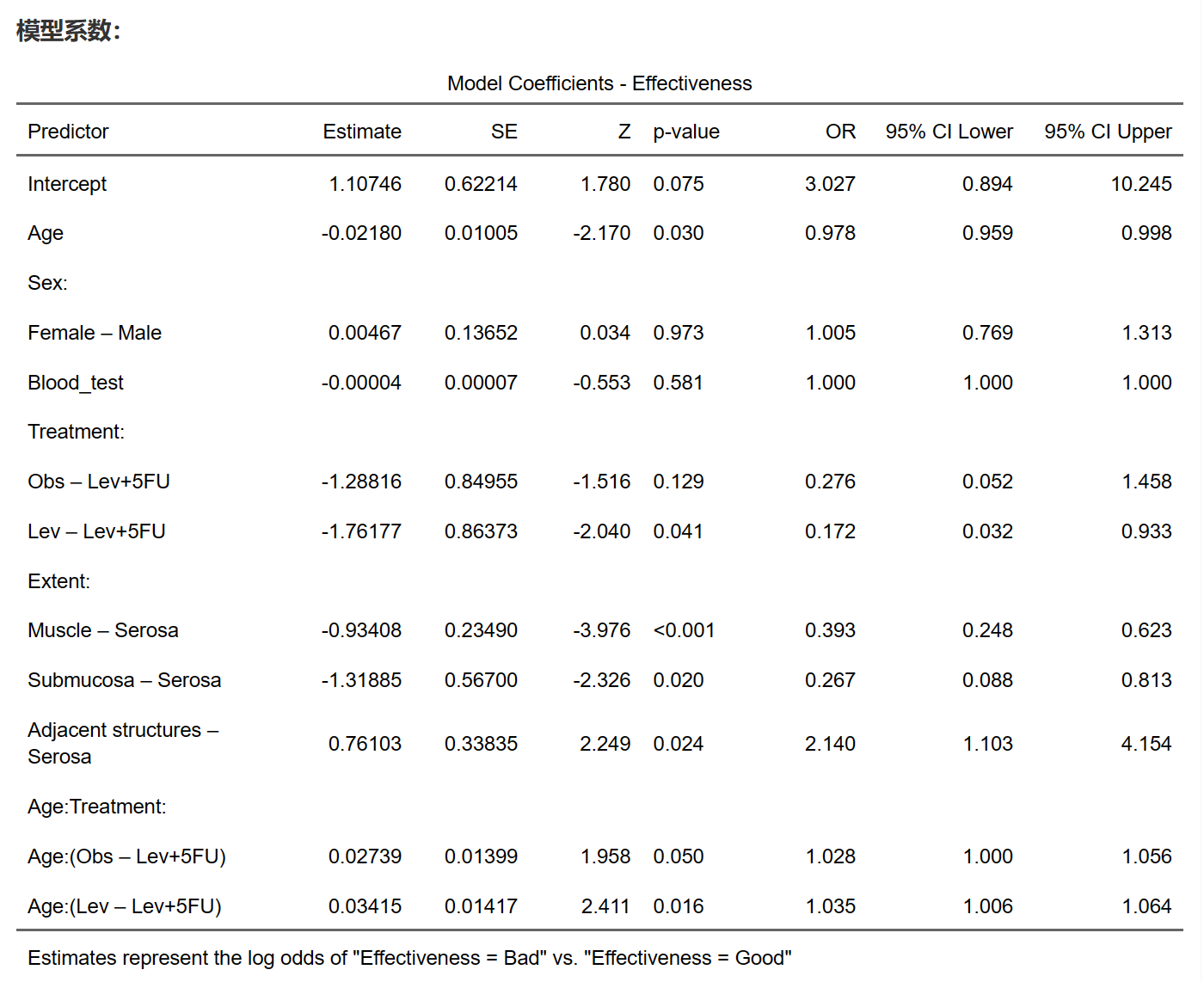
在二分类Logistic回归分析中,对于每个自变量,我们需要估计其对应的参数。参数的估计值反映了自变量与因变量之间的关系。在结果报告中,我们通常可以找到以下信息:
Estimate(估计值):自变量对应的回归系数估计值。系数的正负表示自变量与因变量之间的正负相关关系。系数的绝对值表示了自变量变化一个单位时,对应的log-odds变化的大小。
SE(标准误差):回归系数估计值的标准误差。标准误差是估计值的不确定性度量,用于计算置信区间和进行假设检验。
Z(Z统计量):回归系数估计值除以其标准误差得到的值。Z统计量用于检验回归系数是否显著地不同于零。
p-value(p值):对应于Z统计量的p值。如果p值小于预定显著性水平(例如0.05),我们可以拒绝零假设(即回归系数为0),认为该自变量对因变量具有显著影响。
OR(Odds Ratio,比值比):回归系数的指数形式。比值比表示自变量每增加一个单位时,事件发生几率(Odds)的变化。值大于1表示自变量增加时,事件发生几率增加;值小于1表示自变量增加时,事件发生几率减少;值等于1表示自变量与事件发生几率无关。
95% CI Lower(95%置信区间下限):回归系数的95%置信区间的下限。置信区间表示我们对回归系数的不确定性范围。
95% CI Upper(95%置信区间上限):回归系数的95%置信区间的上限。置信区间表示我们对回归系数的不确定性范围。
总之,这些结果参数帮助我们了解自变量与因变量之间的关系、显著性和不确定性。通过分析这些参数,我们可以评估自变量对事件发生几率的影响以及其显著性水平。
似然比检验:
在二分类Logistic回归中,Omnibus似然比检验用于评估模型中一个或多个自变量对模型拟合优度的显著性贡献。这种检验通过比较包含某个自变量的完整模型与不包含该自变量的简化模型之间的对数似然差值来进行。差值经过计算后,得到一个χ²统计量,然后根据自由度(df)来计算对应的p值。较低的p值表示在包含该自变量的情况下,模型的拟合优度显著地得到了改善。
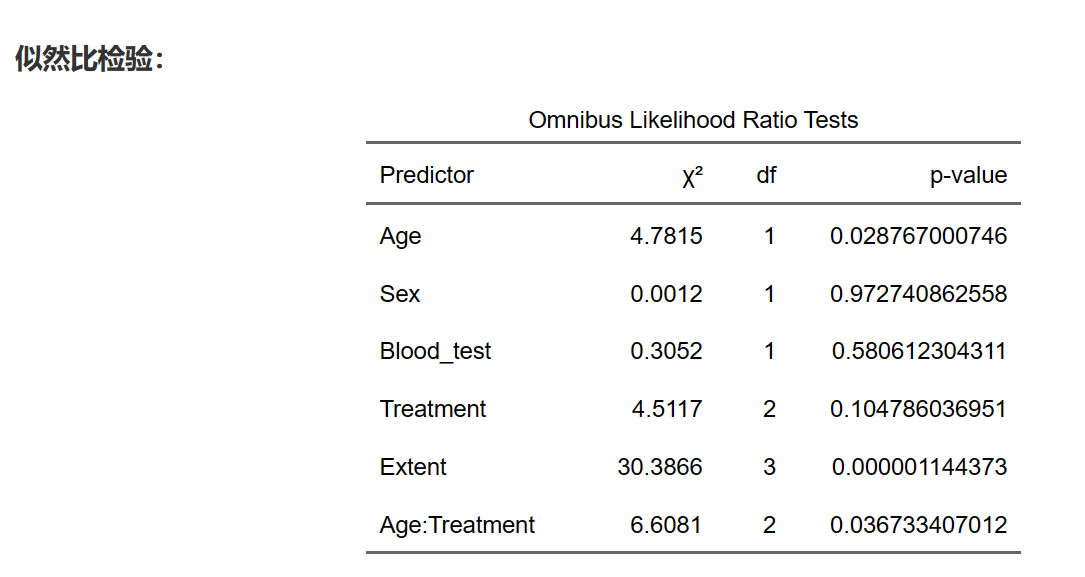
从结果中,我们可以看到不同自变量对模型拟合优度的贡献。例如,年龄(Age)的p值为0.0287,小于0.05,表示年龄对模型的拟合具有显著性贡献。然而,性别(Sex)的p值为0.9727,大于0.05,表明性别对模型的拟合优度没有显著影响。
通过Omnibus似然比检验,我们可以了解到哪些自变量对Logistic回归模型的拟合优度有显著性贡献,从而帮助我们确定关键因素,优化模型和提高预测准确性。
9.18.9 模型拟合评价
选择模型拟合评价的参数:

在Logistic回归分析中,模型拟合优度评价是用于衡量模型与数据之间拟合程度的指标。以下介绍几种常见的Logistic回归模型拟合优度评价指标:
离差(Deviance):离差是基于似然比的一种度量,用于衡量拟合模型与完全拟合模型(即每个观测值都有一个独立参数)之间的差异。较小的离差值表示模型拟合较好。离差值本身无明确标准,通常用于模型间的比较。
AIC(Akaike Information Criterion):AIC是由赤池质量量提出的一种模型选择准则,用于衡量模型拟合优度和模型复杂度之间的平衡。AIC值越小,表示模型拟合较好。AIC主要用于比较不同模型的拟合优度。
计算公式:AIC = -2 * ln(似然比) + 2 * k
其中,k表示模型中参数的个数。
BIC(Bayesian Information Criterion):BIC与AIC类似,也是一种衡量模型拟合优度和模型复杂度之间的平衡的指标。与AIC相比,BIC对模型复杂度的惩罚更大。BIC值越小,表示模型拟合较好。BIC也主要用于比较不同模型的拟合优度。
计算公式:BIC = -2 * ln(似然比) + k * ln(n)
其中,k表示模型中参数的个数,n表示样本量。
伪R²(pseudo-R²):伪R²是Logistic回归中类似于线性回归中R²的指标,用于衡量模型解释力。伪R²的值介于0和1之间,值越接近1,表示模型解释力越强。常见的伪R²有McFadden’s R²、Cox & Snell’s R²和Nagelkerke’s R²。
1)McFadden’s R²:McFadden提出的伪R²,基于空模型(不包含任何自变量)与拟合模型的离差之比。
计算公式:McFadden’s R² = 1 - (拟合模型离差 / 空模型离差)
2)Cox & Snell’s R²:Cox和Snell提出的伪R²,基于空模型和拟合模型的似然比。
计算公式:Cox & Snell’s R² = 1 - (拟合模型似然 / 空模型似然)^(2/n)
其中,n表示样本量。
3)Nagelkerke’s R²:Nagelkerke对Cox & Snell’s R²进行了调整,使其最大值为1,因此在实际应用中更为常用。
计算公式:Nagelkerke’s R² = (Cox & Snell’s R²) / (1 - 空模型似然^(2/n))
其中,n表示样本量。
以上各个参数的定义、意义和评价方法在Logistic回归模型拟合优度评价中都起到了重要作用。在模型评估和选择时,我们需要综合考虑这些指标,以确保选出的模型具有较好的拟合优度和较低的复杂度。需要注意的是,这些指标并非绝对标准,而是用于在多个模型之间进行相对比较。在实际应用中,除了考虑这些指标,还应结合领域知识和研究目标进行模型选择和评估。
模型拟合评价结果如下:
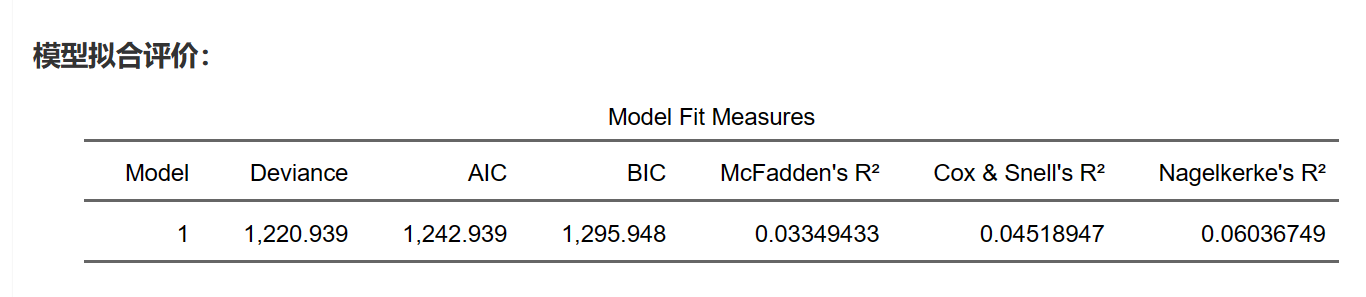
9.18.10 进行估计边际平均值分析:
估计边际平均值(Estimated Marginal Means,EMM)在Logistic回归中是一种描述自变量对因变量(概率)影响的方法。它考虑了其他自变量和交互作用的影响,计算在特定水平或条件下的预测概率。估计边际平均值有助于我们更直观地理解模型中各变量的效应,尤其是在模型中存在交互作用时。
在Logistic回归中,估计边际平均值通常表示某一自变量水平下事件发生的预测概率。这个概率是基于模型中所有其他自变量取其平均值或设定值时的预测值。通过计算不同自变量水平下的估计边际平均值,我们可以比较不同条件下事件发生的可能性。
统计图表在估计边际平均值分析中起到了重要作用。通常,我们使用线图或柱状图展示不同自变量水平下的估计边际平均值,其中横坐标表示自变量的水平,纵坐标表示预测的概率。这样的图表可以帮助我们直观地观察不同自变量水平下事件发生概率的变化,进而分析自变量对事件发生概率的影响。
例如,在一个研究中,我们关心某种药物剂量对患者康复概率的影响,同时需要考虑年龄的影响。在进行Logistic回归分析后,我们可以计算不同药物剂量下的估计边际平均值,并绘制统计图表。图表上的纵坐标表示患者康复的预测概率,横坐标表示药物剂量。通过观察图表,我们可以直观地了解药物剂量与康复概率之间的关系,为临床决策提供依据。
总之,估计边际平均值分析在Logistic回归中具有重要意义,可以帮助我们更好地理解自变量对事件发生概率的影响。通过绘制统计图表,我们可以直观地展示和比较不同自变量水平下的预测概率,从而为实际应用提供依据。
估计边际平均值(Estimated Marginal Means,EMM)分析结果如下:
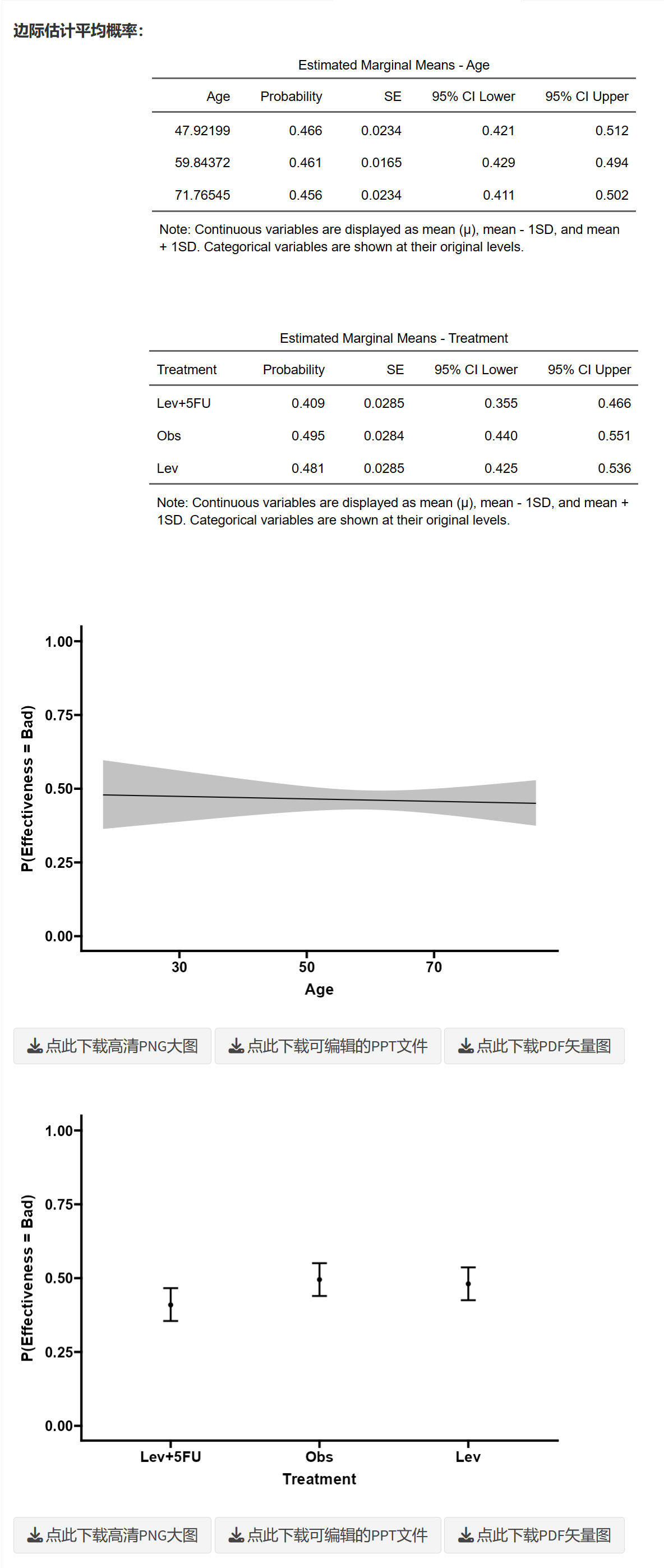
横坐标是自变量的不同取值,纵坐标是结局事件发生的期望概率。期望,就是平均的意思,所以是自变量每个取值患者们,调整了协变量之后的平均概率。
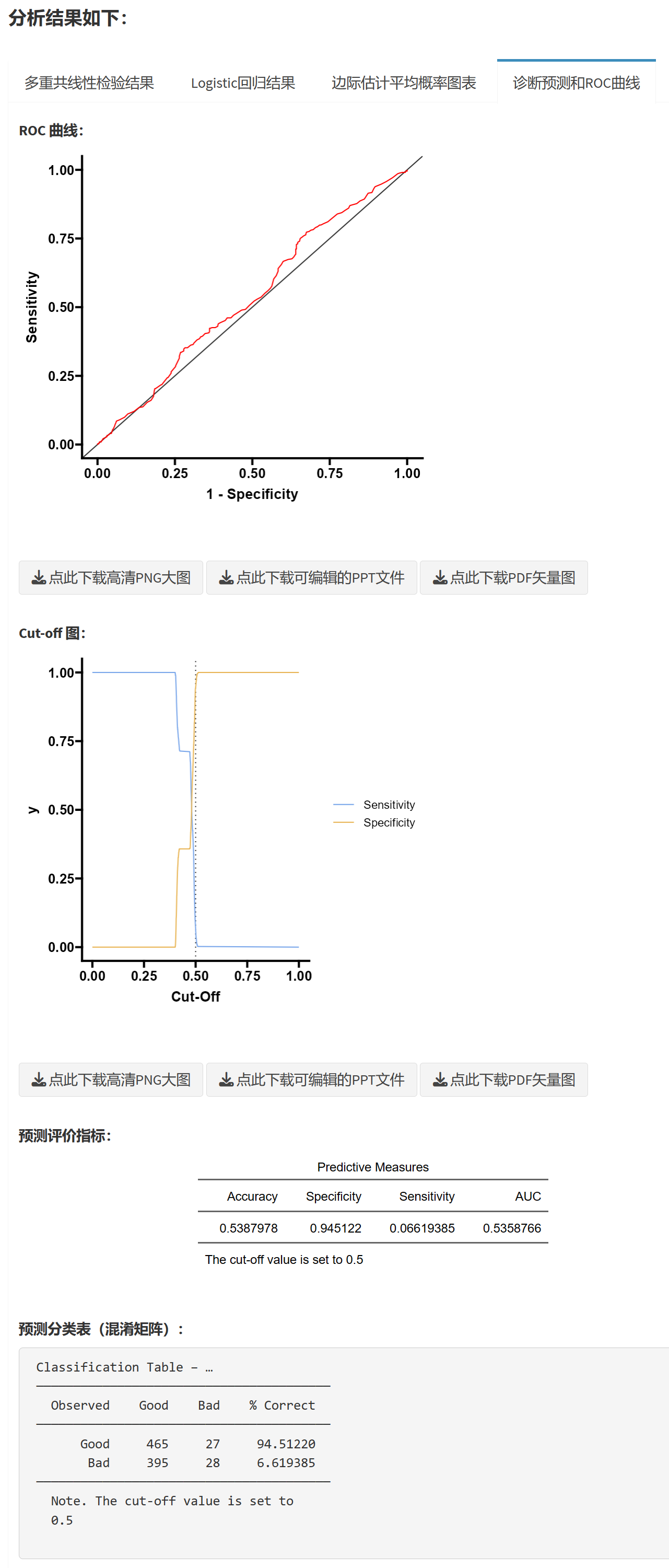
做诊断预测和ROC曲线
Logistic回归的诊断预测主要用于评估模型在预测二分类结果方面的表现。接收者操作特征曲线(ROC曲线)是一种用于评价二分类模型预测性能的图形工具,横坐标表示1-特异度,纵坐标表示灵敏度。ROC曲线下的面积(AUC,Area Under the Curve)越接近1,表示模型的分类预测能力越强。
MSTATA软件界面提供了以下功能,用于评估Logistic回归模型的诊断预测性能:
显示模型的ROC曲线:绘制ROC曲线,直观展示模型在不同截断值下的特异度和灵敏度变化。
显示AUC值:计算ROC曲线下的面积,衡量模型的预测性能。AUC值越接近1,预测性能越好;接近0.5时,预测性能不佳,相当于随机猜测。
设定截断值(cut-off):截断值是一个阈值,用于将预测概率转换为二分类结果。通过调整截断值,可以在特异度和灵敏度之间找到一个平衡。
显示cut-off图:绘制截断值与准确度、特异度、灵敏度之间的关系图,帮助用户选择合适的截断值。
显示预测分类表(混淆矩阵):根据设定的截断值,生成预测分类表,展示真实结果与预测结果的对应关系,包括真阳性(TP)、真阴性(TN)、假阳性(FP)和假阴性(FN)。
显示准确度(Accuracy):计算模型预测结果的准确率,即正确预测的样本占总样本的比例。准确度 = (TP + TN) / (TP + TN + FP + FN)。
显示特异度(Specificity):计算模型在预测阴性样本方面的准确率,即真阴性占所有阴性样本的比例。特异度 = TN / (TN + FP)。
显示灵敏度(Sensitivity):计算模型在预测阳性样本方面的准确率,即真阳性占所有阳性样本的比例。灵敏度 = TP / (TP + FN)。
ROC分析的结果如下:
9.19 有序分类 Logistic 回归(Y 为有序分类变量)
有序分类Logistic回归是一种统计方法,用于研究具有有序分类结果的因变量与一个或多个自变量之间的关系。与普通的Logistic回归不同,有序分类Logistic回归考虑了因变量类别之间的有序关系。这种方法在医学研究和其他领域中非常有用,特别是当因变量具有有序性质时。
以下是一个医学研究中应用有序分类Logistic回归的例子:
假设我们要研究患者的年龄、性别和吸烟状况对心血管疾病风险等级的影响。心血管疾病风险分为三个有序等级:低风险、中风险和高风险。我们的因变量是心血管疾病风险等级,自变量包括年龄、性别和吸烟状况。我们想要了解这些自变量对心血管疾病风险等级的影响。
MSTATA统计软件的有序分类Logistic回归模块提供了以下功能:
设置自变量:可以选择一个或多个自变量,例如年龄、性别和吸烟状况。
支持交互作用项:可以选择是否考虑自变量之间的交互作用。
设置分类自变量的参照水平:可以为分类自变量设置参照水平,以便进行比较。
展示回归系数:展示每个自变量的回归系数,反映其对因变量的影响程度。
展示OR值和可信区间:展示每个自变量的比值比(Odds Ratio,OR)和对应的置信区间,用于衡量自变量对因变量的相对影响。
模型拟合评价:包括Deviance、AIC、BIC、McFadden’s R²、Cox & Snell’s R²、Nagelkerke’s R²等指标,用于评估模型的拟合程度。
进行Omnibus似然比检验:检验模型中所有自变量的整体显著性。
有序分类的阈值(thresholds)分析:展示用于区分不同风险等级的阈值。
导出Word格式的统计报告:将分析结果直接导出为Word文档,便于撰写报告和分享。
9.19.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
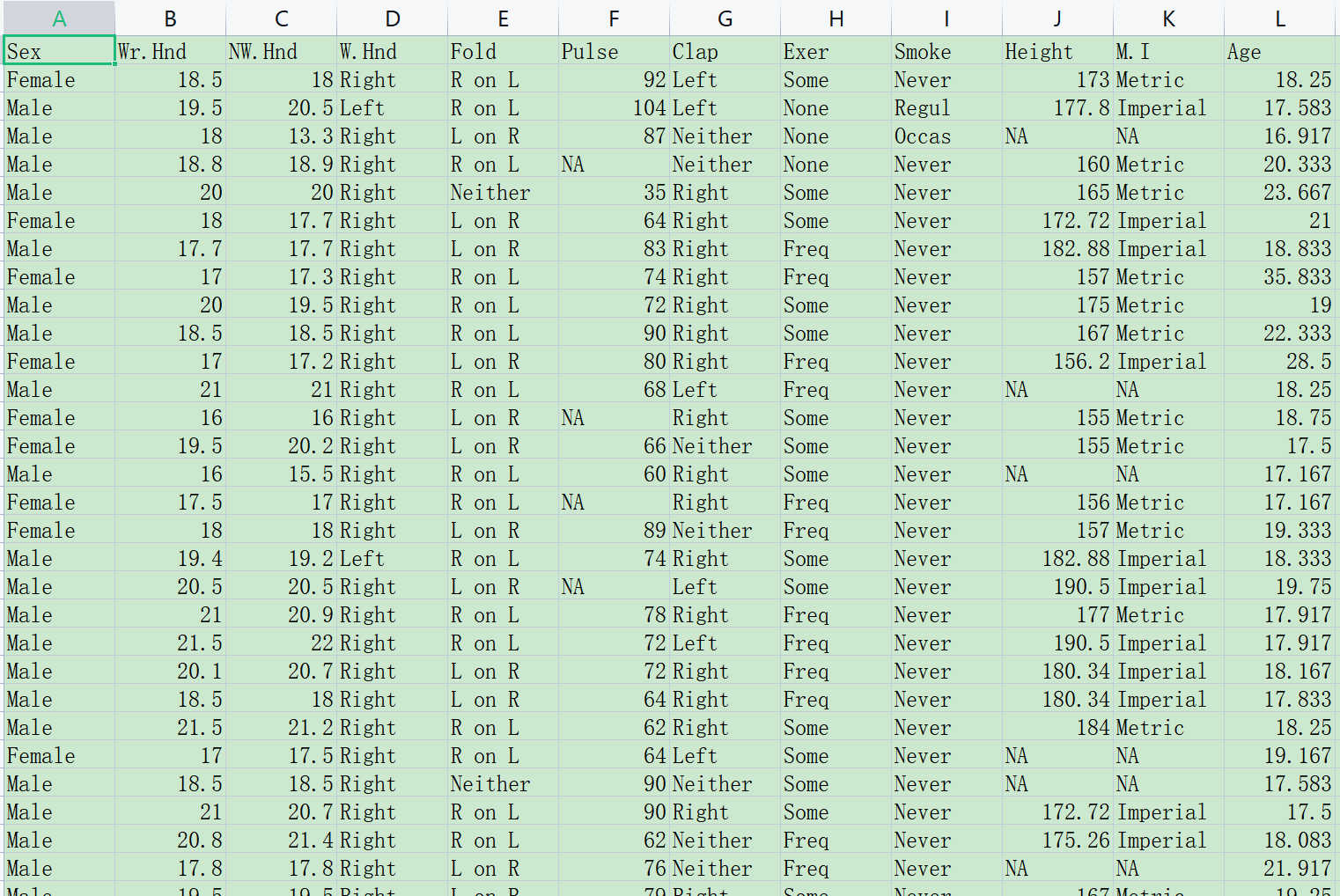
数据集包含了237名学生关于吸烟、锻炼和其他生活方式因素的调查数据。这个数据集包括一个有序分类因变量Exer(锻炼频率),可以将其视为类似于健康状况的有序分类变量。
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
代表结局的应变量:
Exer变量是关于锻炼频率的有序分类变量。它有3个水平,表示不同的锻炼频率:None:不进行锻炼。Some:偶尔锻炼,没有固定的锻炼计划。Freq:经常锻炼,有规律的锻炼计划。
解释变量(自变量):例如上图中的age、sex等等一系列指标。解释(自)变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄\[岁\]、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等)。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
9.19.3 选择结局变量
选择有序分类变量作为应变量进行logistic回归。结局变量不管是 低级-中级-高级 这样的文字,还是 1, 2, 3, 4 这样的数字,都要在前面的页面设置成 factor, 然后在因子顺序设置页面按照从低级到高级的的排列顺序进行拖拽设置。
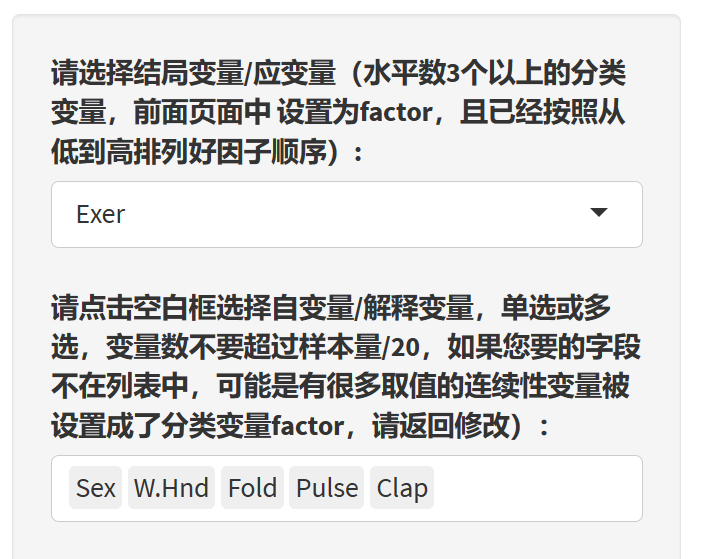
9.19.4 选择解释变量(自变量)
根据提示选择自变量。这里要注意的是,如果上传的数据Excel文件里把连续性变量设置成了字符型,如年龄设置成了字符型,需要在前面”选择字段”功能里改回成numeric,如果按照分类变量放进影响因素分析。同理,如果把ID号也作为分类变量放进影响因素,也会出问题。
另外,在分类变量里,有些亚组人数很少,最好把它和其他亚组合并之后再传上来分析,亚组人数太少容易让可信区间特别宽,影响排版。当然,后续我们也会增加一个合并亚组的小工具。
9.19.5 选择交互作用
点开交互作用选项,点击增加交互作用项按钮,选定两个及以上变量即可生成交互作用项,如果要增加多个交互作用项,重复点击”增加交互作用项”按钮即可;如果选错了,点击重置清零即可。
9.19.8 模型拟合评价
选择模型拟合评价的参数:

在Logistic回归分析中,模型拟合优度评价是用于衡量模型与数据之间拟合程度的指标。以下介绍几种常见的Logistic回归模型拟合优度评价指标:
离差(Deviance):离差是基于似然比的一种度量,用于衡量拟合模型与完全拟合模型(即每个观测值都有一个独立参数)之间的差异。较小的离差值表示模型拟合较好。离差值本身无明确标准,通常用于模型间的比较。
AIC(Akaike Information Criterion):AIC是由赤池质量量提出的一种模型选择准则,用于衡量模型拟合优度和模型复杂度之间的平衡。AIC值越小,表示模型拟合较好。AIC主要用于比较不同模型的拟合优度。
计算公式:AIC = -2 * ln(似然比) + 2 * k
其中,k表示模型中参数的个数。
BIC(Bayesian Information Criterion):BIC与AIC类似,也是一种衡量模型拟合优度和模型复杂度之间的平衡的指标。与AIC相比,BIC对模型复杂度的惩罚更大。BIC值越小,表示模型拟合较好。BIC也主要用于比较不同模型的拟合优度。
计算公式:BIC = -2 * ln(似然比) + k * ln(n)
其中,k表示模型中参数的个数,n表示样本量。
伪R²(pseudo-R²):伪R²是Logistic回归中类似于线性回归中R²的指标,用于衡量模型解释力。伪R²的值介于0和1之间,值越接近1,表示模型解释力越强。常见的伪R²有McFadden’s R²、Cox & Snell’s R²和Nagelkerke’s R²。
1)McFadden’s R²:McFadden提出的伪R²,基于空模型(不包含任何自变量)与拟合模型的离差之比。
计算公式:McFadden’s R² = 1 - (拟合模型离差 / 空模型离差)
2)Cox & Snell’s R²:Cox和Snell提出的伪R²,基于空模型和拟合模型的似然比。
计算公式:Cox & Snell’s R² = 1 - (拟合模型似然 / 空模型似然)^(2/n)
其中,n表示样本量。
3)Nagelkerke’s R²:Nagelkerke对Cox & Snell’s R²进行了调整,使其最大值为1,因此在实际应用中更为常用。
计算公式:Nagelkerke’s R² = (Cox & Snell’s R²) / (1 - 空模型似然^(2/n))
其中,n表示样本量。
以上各个参数的定义、意义和评价方法在Logistic回归模型拟合优度评价中都起到了重要作用。在模型评估和选择时,我们需要综合考虑这些指标,以确保选出的模型具有较好的拟合优度和较低的复杂度。需要注意的是,这些指标并非绝对标准,而是用于在多个模型之间进行相对比较。在实际应用中,除了考虑这些指标,还应结合领域知识和研究目标进行模型选择和评估。
模型拟合评价结果如下:
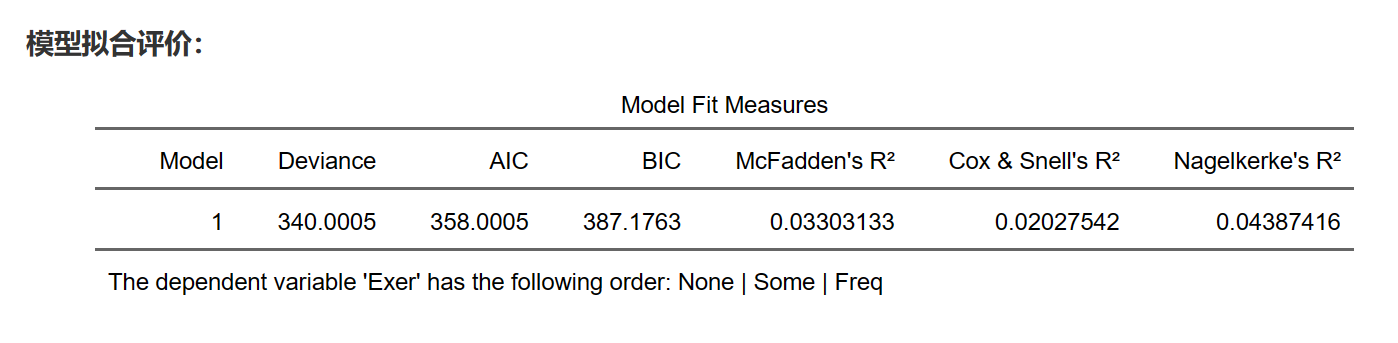
9.19.9 Omnibus 似然比检验
Omnibus Likelihood Ratio Tests(全模型似然比检验)是一种用于评估自变量对有序分类Logistic回归模型的整体显著性的方法。它通过比较包含所有自变量的完整模型与一个不包含任何自变量的空模型(即只包含截距项)之间的似然比来检验自变量的整体显著性。基本上,它在回答这个问题:“我们的模型是否比一个不包含任何预测变量的模型更好地拟合数据?”

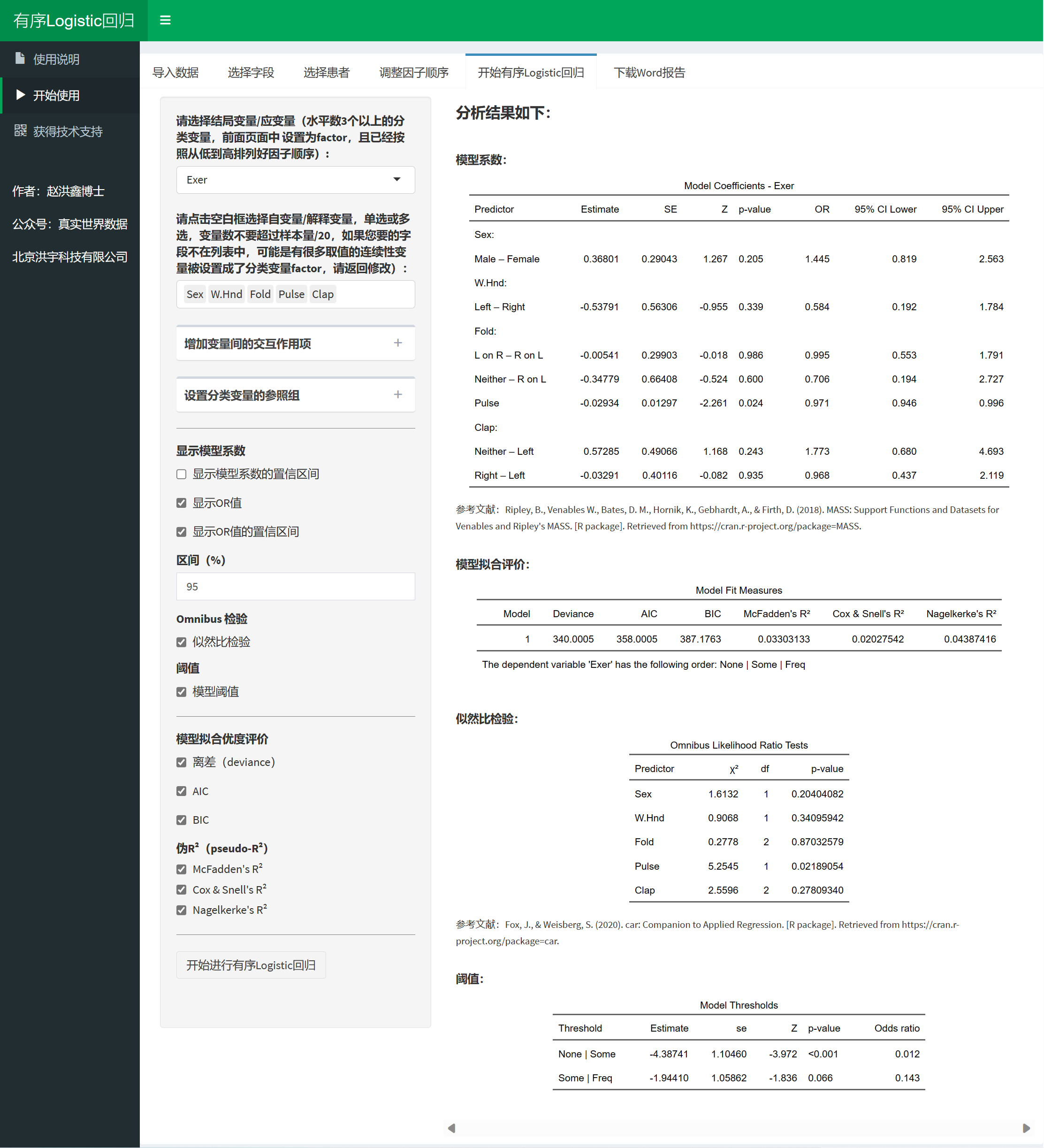
Omnibus 检验结果如下:
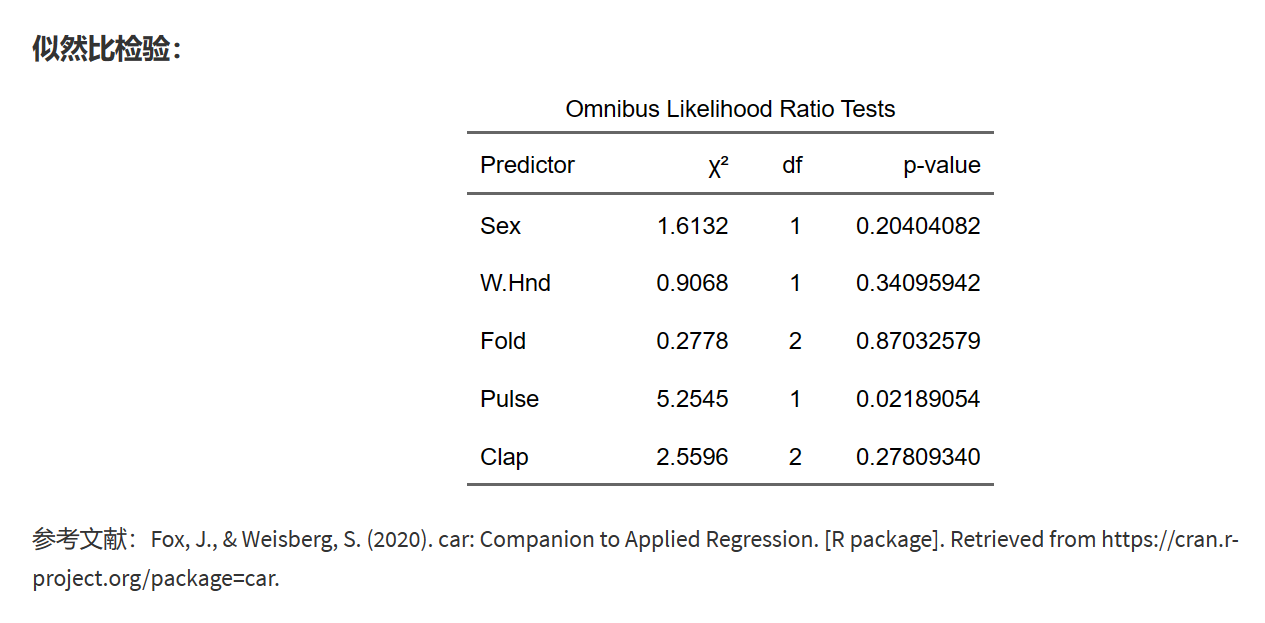
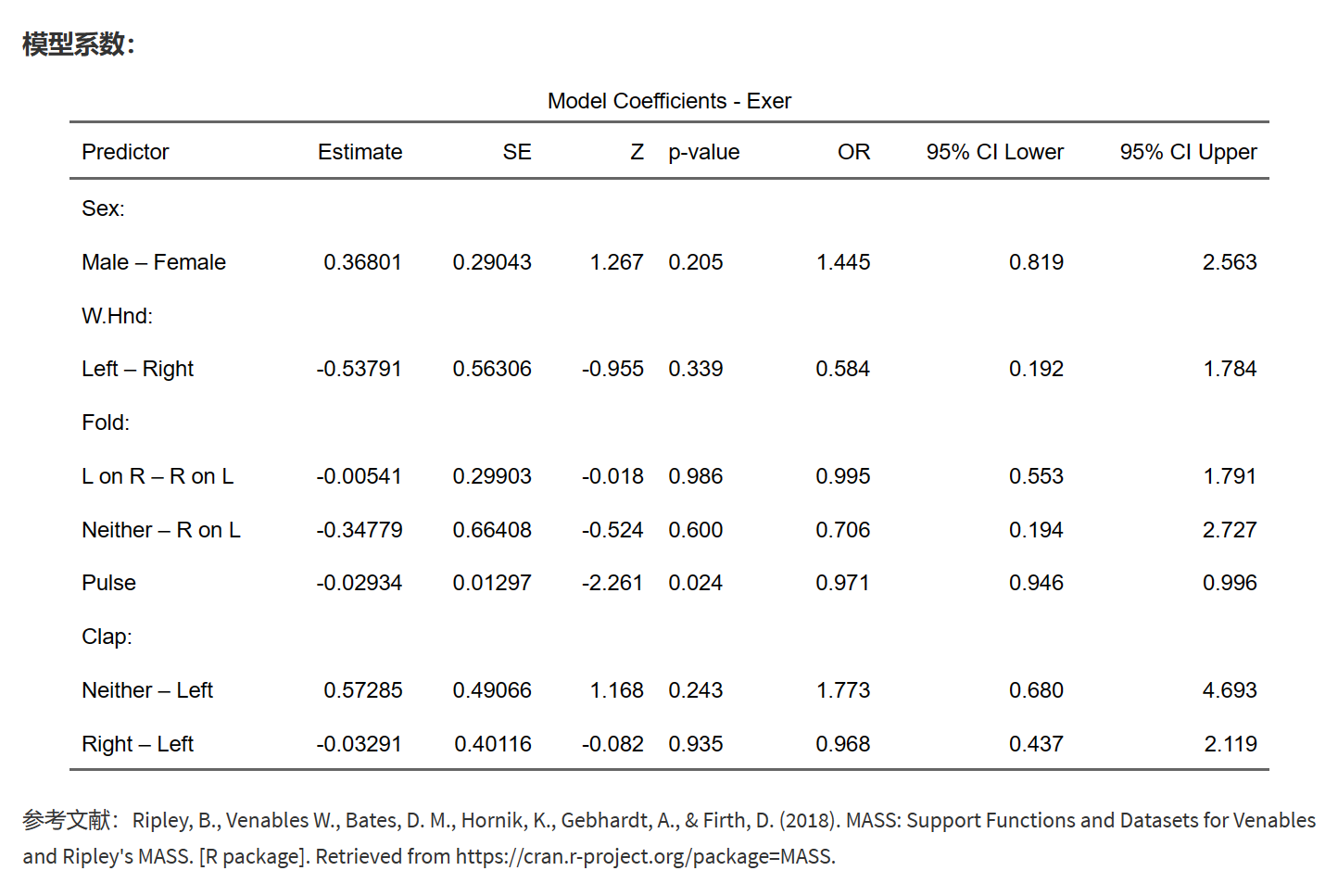
在上面的输出中,我们看到了五个自变量(Sex、W.Hnd、Fold、Pulse和Clap)的Omnibus Likelihood Ratio Tests结果。这些结果包括以下信息:
χ²:似然比统计量(Likelihood Ratio Test statistic),用于比较完整模型和空模型。
df:自由度(degrees of freedom),等于该自变量的分类水平数减1。对于二分类自变量,自由度为1;对于多分类自变量,自由度等于水平数减1。
p-value:对应于似然比统计量的p值。如果p值小于预定显著性水平(例如0.05),我们可以拒绝零假设(即自变量对模型没有显著影响),认为自变量对模型具有显著性。
在这个例子中,我们可以看到:
Sex:χ² = 1.6132,df = 1,p-value = 0.20404082。p值大于0.05,因此性别对模型的影响不显著。
W.Hnd:χ² = 0.9068,df = 1,p-value = 0.34095942。p值大于0.05,因此惯用手对模型的影响不显著。
Fold:χ² = 0.2778,df = 2,p-value = 0.87032579。p值大于0.05,因此fold对模型的影响不显著。
Pulse:χ² = 5.2545,df = 1,p-value = 0.02189054。p值小于0.05,因此脉搏对模型的影响显著。
Clap:χ² = 2.5596,df = 2,p-value = 0.27809340。p值大于0.05,因此clap对模型的影响不显著。
总之,Omnibus Likelihood Ratio Tests可以帮助我们评估每个自变量对有序分类Logistic回归模型的整体显著性,从而了解哪些自变量对模型具有显著影响。
9.19.10 阈值(Threshold)参数分析结果:
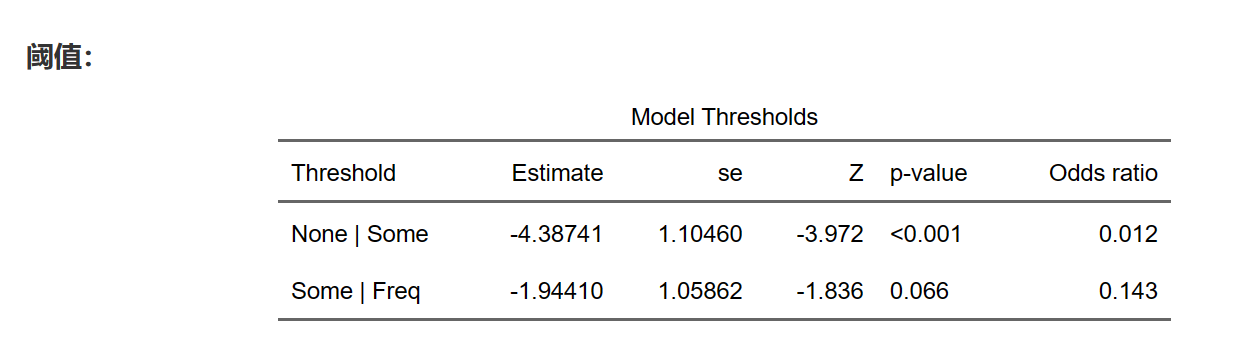
阈值结果显示有序分类Logistic回归模型的阈值参数估计。阈值参数是用于将模型的预测值(线性组合的结果)转换为概率,以便将观测值分类到有序类别中。在有序分类Logistic回归中,我们通常需要估计K-1个阈值参数,其中K表示因变量的类别数。这些阈值参数定义了模型中的切分点,用于将预测值转换为概率。
在这个例子中,我们有两个阈值参数:None | Some(无锻炼和少量锻炼之间的阈值)和Some | Freq(少量锻炼和频繁锻炼之间的阈值)。对于每个阈值参数,报告包括以下信息:
Estimate:阈值参数的估计值。
se:阈值参数估计值的标准误差。
Z:Z统计量,是阈值参数估计值除以标准误差得到的值。
p-value:对应于Z统计量的p值。如果p值小于预定显著性水平(例如0.05),我们可以拒绝零假设(即阈值参数为0),认为该阈值具有显著性。
Odds ratio:表示阈值参数的比值。在这种情况下,它显示了跨越阈值时相对风险的变化。值大于1表示风险增加,值小于1表示风险减少。
在这个例子中,我们可以看到:
None | Some 阈值:
Estimate:-4.38741
se:1.10460
Z:-3.972
p-value:<0.001,表示该阈值具有显著性。
Odds ratio:0.012,表示跨越这个阈值时,相对风险减少。
Some | Freq 阈值:
Estimate:-1.94410
se:1.05862
Z:-1.836
p-value:0.066,表示该阈值的显著性较弱。
Odds ratio:0.143,表示跨越这个阈值时,相对风险减少。
总之,阈值结果报告帮助我们了解有序分类Logistic回归模型中的切分点,以便将预测值转换为概率并将观测值分类到有序类别中。同时,它们也可以帮助我们评估跨越阈值时相对风险的变化。
9.20 无序分类 Logistic 回归(Y 为无序分类变量)
无序分类Logistic回归是一种统计方法,用于研究具有无序分类结果的因变量与一个或多个自变量之间的关系。与有序分类Logistic回归不同,无序分类Logistic回归并不考虑因变量类别之间的有序关系。这种方法在医学研究和其他领域中非常有用,特别是当因变量是分类的、并且分类之间没有明显的顺序关系时。
以下是一个医学研究中应用无序分类Logistic回归的例子:
假设我们要研究患者的年龄、性别和吸烟状况对心血管疾病类型的影响。心血管疾病类型可以分为冠状动脉疾病、心肌梗死、心脏瓣膜病等,这些类别之间没有明显的有序关系。我们的因变量是心血管疾病类型,自变量包括年龄、性别和吸烟状况。我们想要了解这些自变量对心血管疾病类型的影响。
MSTATA统计软件的无序分类Logistic回归模块提供了以下功能:
设置自变量:可以选择一个或多个自变量,例如年龄、性别和吸烟状况。
支持交互作用项:可以选择是否考虑自变量之间的交互作用。
设置分类自变量的参照水平:可以为分类自变量设置参照水平,以便进行比较。
展示回归系数:展示每个自变量的回归系数,反映其对因变量的影响程度。
展示OR值和可信区间:展示每个自变量的比值比(Odds Ratio,OR)和对应的置信区间,用于衡量自变量对因变量的相对影响。
模型拟合评价:包括Deviance、AIC、BIC、伪R²(pseudo-R²)、McFadden’s R²、Cox & Snell’s R²、Nagelkerke’s R²等指标,用于评估模型的拟合程度。
进行Omnibus似然比检验:检验模型中所有自变量的整体显著性。
无序分类的概率分析:展示每个因变量类别的概率,以及各个类别之间的相对关系。
生成估计边际平均概率统计图表:可以清晰地看到各自变量在模型中的作用效果。
导出Word格式的统计报告:将分析结果直接导出为Word文档,便于撰写报告和分享。这包括模型的系数、模型的拟合优度指标、OR值及其置信区间等关键信息。此外,报告中还会包含估计边际平均概率的统计图表,以便于直观地理解和解释模型的结果。
9.20.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
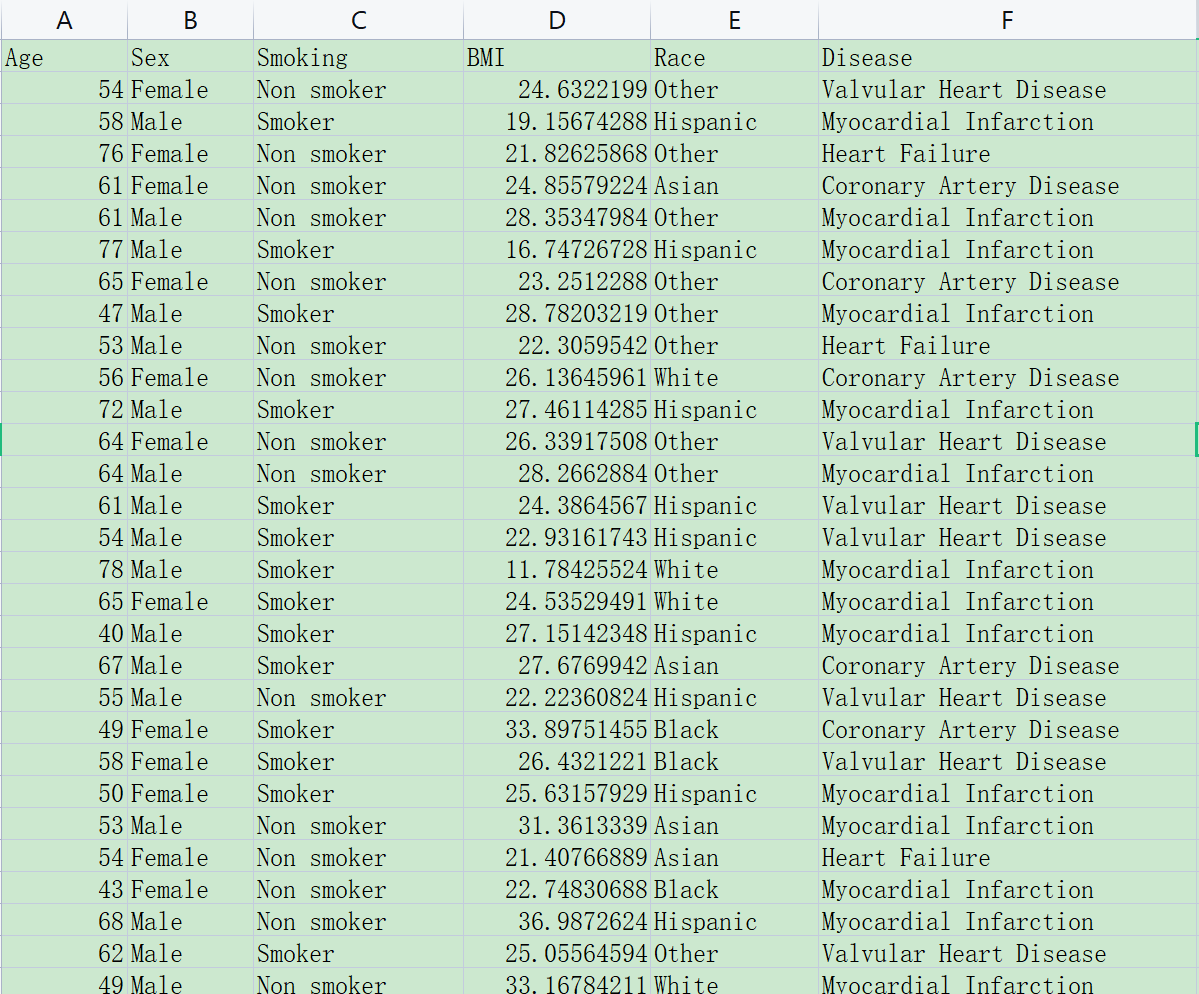
数据集遵循以下规则:
每一行代表一个患者,这是准备数据的最重要前提。
我们的因变量,即我们想要预测的变量是’Disease’,它是一个无序分类变量,表示患者的心血管疾病类型,有”Coronary Artery Disease”、“Myocardial Infarction”、“Valvular Heart Disease”、“Heart Failure”四种情况。
自变量,也就是解释变量包括年龄(Age),性别(Sex),吸烟状态(Smoking),体重指数(BMI)和种族(Race)等。这些变量有连续性变量和分类变量两种类型:
连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值):在本数据集中,’Age’和’BMI’是连续性变量。’Age’表示患者的年龄,’BMI’表示患者的身体质量指数。
分类变量(是说明事物类别的一个名称,其取值是分类数据):在本数据集中,‘Sex’,’Smoking’和’Race’是分类变量。’Sex’表示患者的性别,其变量值为”Male”或”Female”;’Smoking’表示患者的吸烟状态,其变量值为”Non smoker”或”Smoker”;’Race’也是一个分类变量,其变量值可以为”Asian”、“Black”、“White”、“Hispanic”或”Other”。
理解这些概念非常重要,因为在后面的分析中,我们需要针对不同类型的变量进行不同的处理。
9.20.4 选择解释变量(自变量)
根据提示选择自变量。这里要注意的是,如果上传的数据Excel文件里把连续性变量设置成了字符型,如年龄设置成了字符型,需要在前面”选择字段”功能里改回成numeric,如果按照分类变量放进影响因素分析。同理,如果把ID号也作为分类变量放进影响因素,也会出问题。
另外,在分类变量里,有些亚组人数很少,最好把它和其他亚组合并之后再传上来分析,亚组人数太少容易让可信区间特别宽,影响排版。当然,后续我们也会增加一个合并亚组的小工具。
9.20.5 选择交互作用
点开交互作用选项,点击增加交互作用项按钮,选定两个及以上变量即可生成交互作用项,如果要增加多个交互作用项,重复点击”增加交互作用项”按钮即可;如果选错了,点击重置清零即可。这个案例中我们不选交互作用。
9.20.7 Logistic回归结果展示选项
选择结果展示的表格外观:
可以选择是否显示回归系数的置信区间、是否显示OR值,是否显示OR值的置信区间,以及是否做似然比检验。
回归分析结果如下:
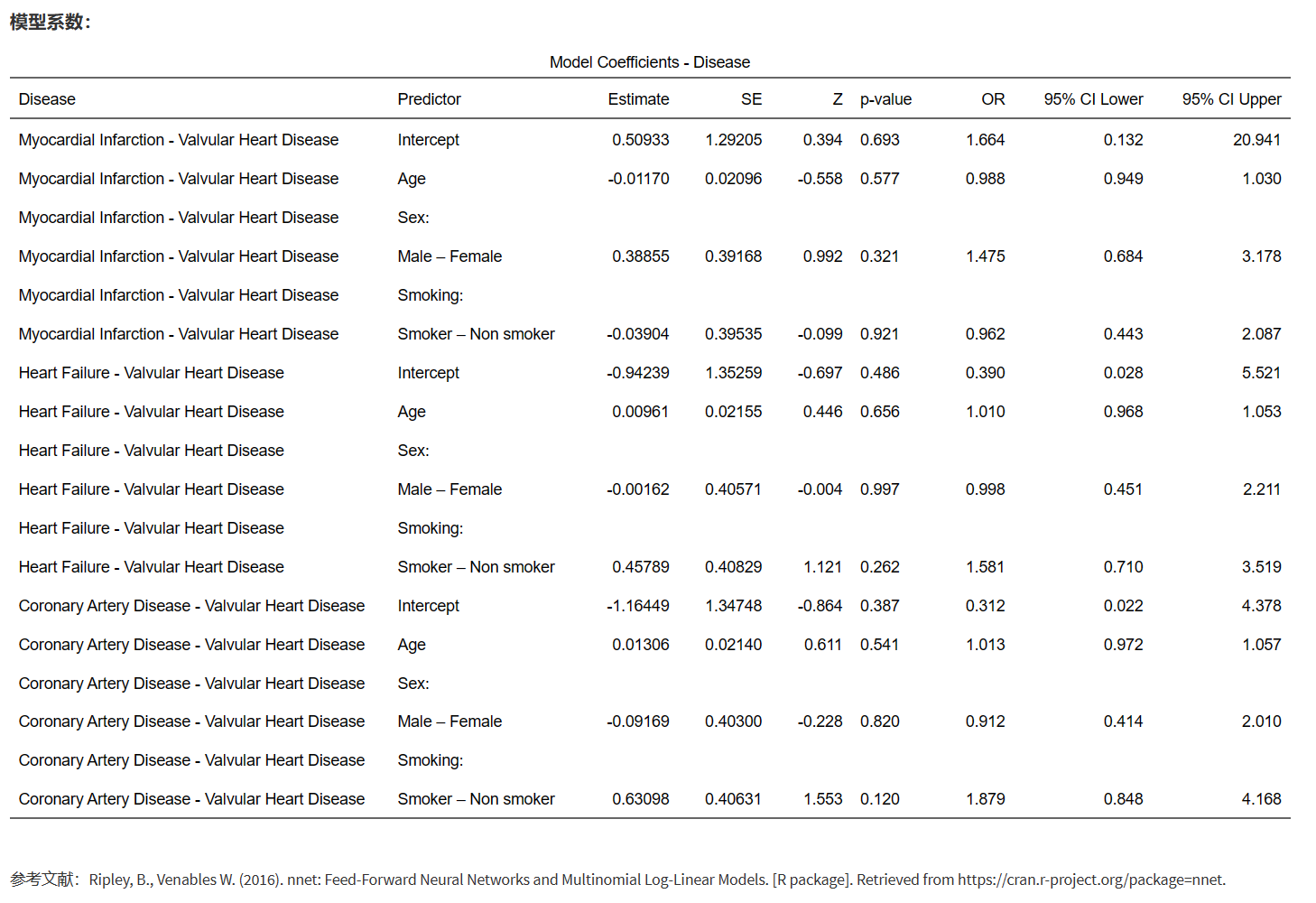
这个统计结果是一个多项式Logistic回归的输出结果,用于分析心血管疾病类型与年龄、性别和吸烟状态的关系。在多项式Logistic回归中,我们会选择一个参照类别,这里选择的是”Valvular Heart Disease”,然后其他的类别都会与这个参照类别进行比较。
以下是对表格中参数的解释:
Estimate: 这是回归系数,代表了当解释变量增加一个单位时,log odds的变化量。例如,在”Coronary Artery Disease - Valvular Heart Disease”中,年龄的Estimate值为0.01306,表示每增加一岁,患冠状动脉疾病相对于患心脏瓣膜病的log odds将增加0.01306。
SE: 这是标准误,衡量的是回归系数的不确定性。标准误越小,估计的准确度越高。
Z: 这是Z统计量,是回归系数除以其标准误的结果。在大样本中,Z统计量服从标准正态分布。
p-value: 这是Z统计量对应的p值。p值小于0.05通常被认为是统计显著的,这意味着我们拒绝零假设(解释变量对因变量没有影响),认为解释变量对因变量有影响。
OR (Odds Ratio): 这是比值比,表示当解释变量增加一个单位时,odds的倍数变化。例如,在”Coronary Artery Disease - Valvular Heart Disease”中,年龄的OR值为1.013,表示每增加一岁,患冠状动脉疾病相对于患心脏瓣膜病的odds将增加1.3%。
95% CI Lower & 95% CI Upper: 这是回归系数的95%置信区间。如果置信区间包含0,那么我们通常认为这个回归系数不是统计显著的。
注意:以上解释是在所有其他变量不变的情况下进行的。另外,由于这是无序分类logistic回归,因此,不同类型疾病之间的比较(例如,冠状动脉疾病和心肌梗死之间的比较)可能没有意义。
似然比检验:

Omnibus Likelihood Ratio Tests 用于评估自变量对模型的贡献度。这个统计表中的每一行对应一个自变量。χ²值表示该自变量的似然比检验统计量,df是自由度,p-value是似然比检验的p值。
Age:这一行的结果显示,年龄这个自变量在模型中的影响不显著(p值=0.662,大于0.05)。这意味着,在控制其他因素的情况下,年龄对心脏病发病类型的影响不显著。
Sex:这一行的结果显示,性别这个自变量在模型中的影响不显著(p值=0.630,大于0.05)。这意味着,在控制其他因素的情况下,性别对心脏病发病类型的影响不显著。
Smoking:这一行的结果显示,吸烟状态这个自变量在模型中的影响不显著(p值=0.257,大于0.05)。这意味着,在控制其他因素的情况下,吸烟状态对心脏病发病类型的影响不显著。
这个结果表明,在考虑其他变量的影响后,年龄、性别和吸烟状态在这个模型中对心脏病类型的预测并没有显著贡献。也就是说,我们不能确认这些变量对于预测心脏病类型具有显著的统计意义。
需要注意的是,这并不意味着这些变量在实际中对心脏病类型没有影响。可能是由于样本数量不足、变量间的关系复杂或者存在其他未考虑到的混淆因素等原因,导致在这个模型中这些变量的影响没有达到统计显著水平。因此,在做出结论时需要综合考虑统计结果和实际情况。
9.20.8 模型拟合评价
选择模型拟合评价的参数:

在Logistic回归分析中,模型拟合优度评价是用于衡量模型与数据之间拟合程度的指标。以下介绍几种常见的Logistic回归模型拟合优度评价指标:
离差(Deviance):离差是基于似然比的一种度量,用于衡量拟合模型与完全拟合模型(即每个观测值都有一个独立参数)之间的差异。较小的离差值表示模型拟合较好。离差值本身无明确标准,通常用于模型间的比较。
AIC(Akaike Information Criterion):AIC是由赤池质量量提出的一种模型选择准则,用于衡量模型拟合优度和模型复杂度之间的平衡。AIC值越小,表示模型拟合较好。AIC主要用于比较不同模型的拟合优度。
计算公式:AIC = -2 * ln(似然比) + 2 * k
其中,k表示模型中参数的个数。
BIC(Bayesian Information Criterion):BIC与AIC类似,也是一种衡量模型拟合优度和模型复杂度之间的平衡的指标。与AIC相比,BIC对模型复杂度的惩罚更大。BIC值越小,表示模型拟合较好。BIC也主要用于比较不同模型的拟合优度。
计算公式:BIC = -2 * ln(似然比) + k * ln(n)
其中,k表示模型中参数的个数,n表示样本量。
伪R²(pseudo-R²):伪R²是Logistic回归中类似于线性回归中R²的指标,用于衡量模型解释力。伪R²的值介于0和1之间,值越接近1,表示模型解释力越强。常见的伪R²有McFadden’s R²、Cox & Snell’s R²和Nagelkerke’s R²。
1)McFadden’s R²:McFadden提出的伪R²,基于空模型(不包含任何自变量)与拟合模型的离差之比。
计算公式:McFadden’s R² = 1 - (拟合模型离差 / 空模型离差)
2)Cox & Snell’s R²:Cox和Snell提出的伪R²,基于空模型和拟合模型的似然比。
计算公式:Cox & Snell’s R² = 1 - (拟合模型似然 / 空模型似然)^(2/n)
其中,n表示样本量。
3)Nagelkerke’s R²:Nagelkerke对Cox & Snell’s R²进行了调整,使其最大值为1,因此在实际应用中更为常用。
计算公式:Nagelkerke’s R² = (Cox & Snell’s R²) / (1 - 空模型似然^(2/n))
其中,n表示样本量。
以上各个参数的定义、意义和评价方法在Logistic回归模型拟合优度评价中都起到了重要作用。在模型评估和选择时,我们需要综合考虑这些指标,以确保选出的模型具有较好的拟合优度和较低的复杂度。需要注意的是,这些指标并非绝对标准,而是用于在多个模型之间进行相对比较。在实际应用中,除了考虑这些指标,还应结合领域知识和研究目标进行模型选择和评估。
模型拟合评价结果如下:

9.20.9 进行估计边际平均值分析:
在统计学中,边际平均值(Estimated Marginal Means,EMM)有时也被称为预期平均值或调整平均值。在无序logistic回归中,EMM是当所有其他自变量被控制在其平均水平时,某一特定自变量取某一特定值的预期因变量平均值。
例如,假设我们在无序logistic回归模型中有年龄、性别和吸烟状态三个自变量,疾病类型是因变量。在计算EMM时,我们可能对男性(性别)的预期疾病类型进行估计,同时将年龄控制在所有样本的平均年龄,吸烟状态控制在样本的平均吸烟状态。这样我们就得到了在平均年龄和平均吸烟状态下,男性的预期疾病类型概率的平均值。
EMM的主要应用在于它可以帮助我们理解和解释一个复杂的统计模型。通过比较不同水平的EMM,我们可以了解不同条件下的预期结果。这在研究中非常有用,尤其是当我们关注的是多种因素同时影响结果时。
估计边际平均值(Estimated Marginal Means,EMM)分析结果如下:
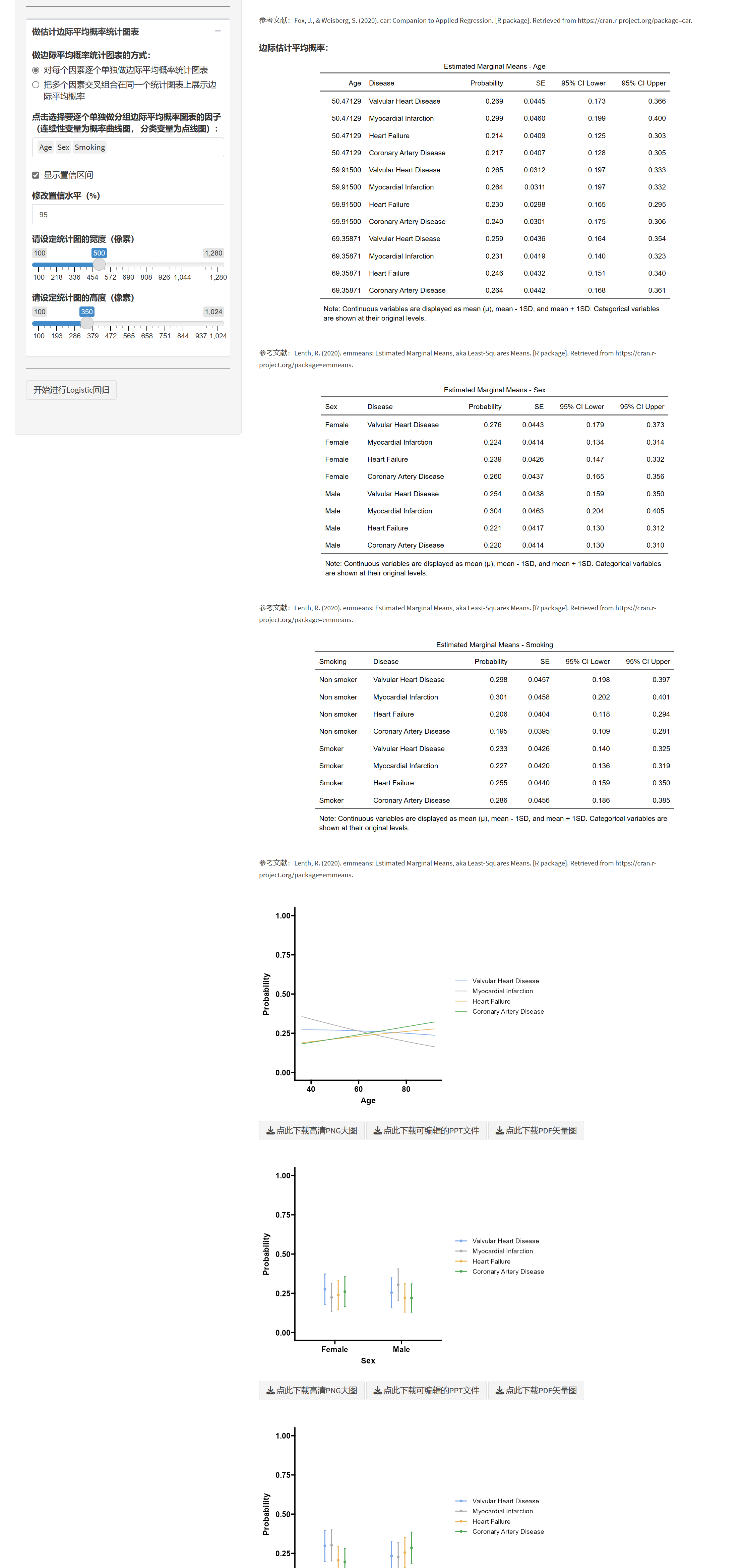
以年龄为例:
这个表格提供了在三种不同年龄水平(平均年龄,平均年龄减去一个标准差,和平均年龄加上一个标准差)下,患有四种不同疾病(二尖瓣疾病,心肌梗塞,心力衰竭,和冠状动脉疾病)的估计边际概率。这个概率的含义是,在给定年龄的情况下,患者被诊断为某种疾病的概率。这里的”年龄”是一个连续变量,被设定为三个水平:平均值,平均值减去一个标准差,和平均值加上一个标准差。
对于每一种疾病和年龄组合,表格提供了以下信息:
概率(Probability):在给定年龄的情况下,被诊断为某种疾病的估计概率。例如,对于年龄为50.47129岁的人,被诊断为二尖瓣疾病的概率估计为0.269。
标准误(SE):概率估计的标准误,可以理解为概率估计的不确定性。标准误越小,估计的概率越精确。
95%置信区间(95% CI Lower,95% CI Upper):这个区间表示,真实的概率有95%的可能性落在这个区间内。例如,对于年龄为50.47129岁的人,被诊断为二尖瓣疾病的真实概率有95%的可能性在0.173到0.366之间。
这个表格可以帮助我们理解年龄如何影响患有不同疾病的概率。例如,从表格中我们可以看出,对于年龄在50.47129岁和69.35871岁之间的人,他们患有心肌梗塞的概率估计从0.299下降到0.231。这可能暗示年龄对患有心肌梗塞的风险有一定的影响。然而,要得出这个结论,我们还需要进一步的统计检验来确认年龄的效应是否显著。
9.21 广义线性模型(非常强大,医学研究首选推荐)
广义线性模型是一类非常重要的统计模型,它广泛应用于各种科学研究领域。广义线性模型是线性模型的推广,它允许因变量服从任意指数分布族,通过引入链接函数来描述因变量与自变量之间的关系。这使得广义线性模型可以适用于更加广泛的情况,例如因变量是二项分布、泊松分布等情况。
例如,在医学研究中,我们可能关注某种疾病的发生率是否与特定的风险因素有关。此时,我们的因变量是二项分布(患病与否),自变量是风险因素(如年龄、性别、吸烟与否等),通过广义线性模型,我们可以有效地建立因变量与自变量之间的关系,从而探索特定风险因素对疾病发生的影响。
MSTATA是一款强大的统计软件,它提供了广义线性模型模块,可以用于估计具有类别和/或连续因变量和自变量的广义线性模型,还提供了各种选项来方便用户估计交互作用、简单斜率、简单效应等。
MSTATA可以估计多种线性模型,包括线性模型、泊松模型、超分散泊松模型、负二项模型、Logistic模型、Probit模型、序数模型(比例比模型)、多项式模型,以及可以自定义分布和链接函数的模型。
各个模型根据链接函数和因变量的分布来定义,从而可以模型不同类型的因变量。例如,线性模型使用身份链接函数和高斯分布,可以用于连续因变量的一般线性模型。
MSTATA支持的分布有:高斯分布、二项分布、伽马分布、逆高斯分布。支持的链接函数有:身份、对数、逆函数、逆平方函数。虽然软件不会检查分布/链接函数组合的合理性,但如果数据不符合选定的自定义模型,将会发出错误信息。
MSTATA支持的功能有:设置模型、设置分布、设置链接函数、设置交互作用、设置分类变量参照组、设置连续性变量转换和标化、设置Contrast分析编码、进行事后检验、多重比较P值调整、进行简单效应(Simple effect)分析、进行边际估计均值(LSmeans、事件发生概率等)分析、绘制统计图。



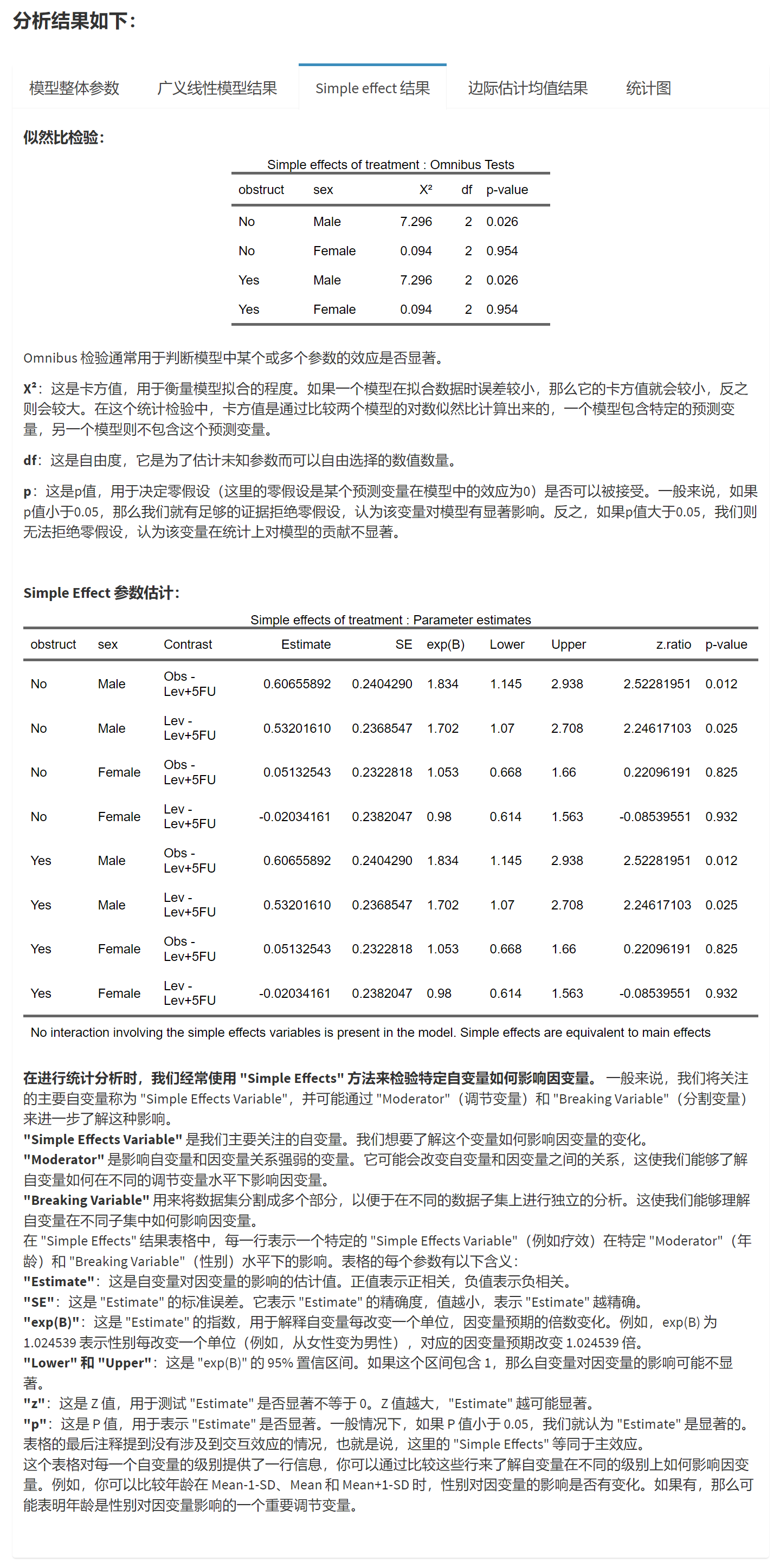
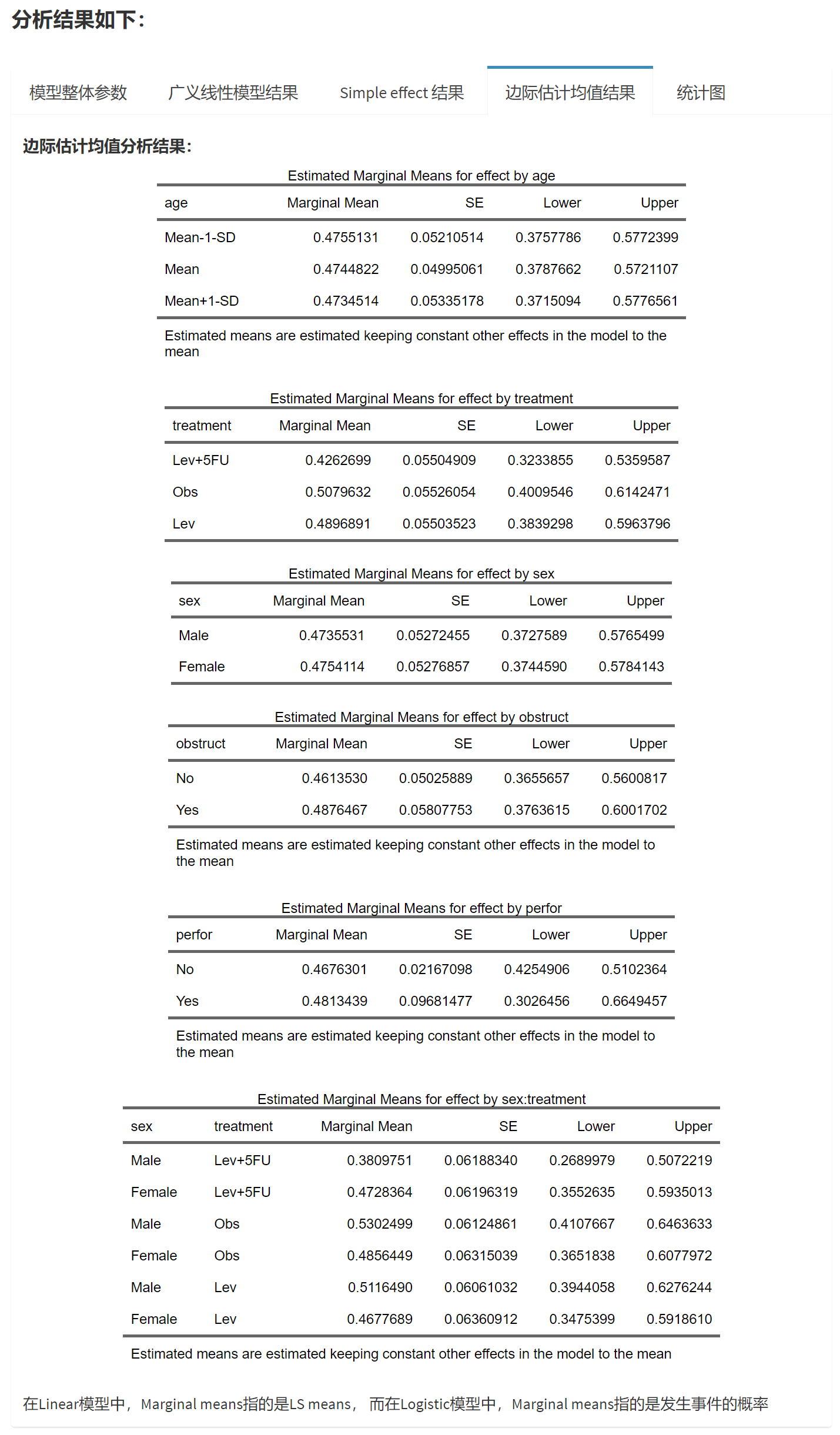
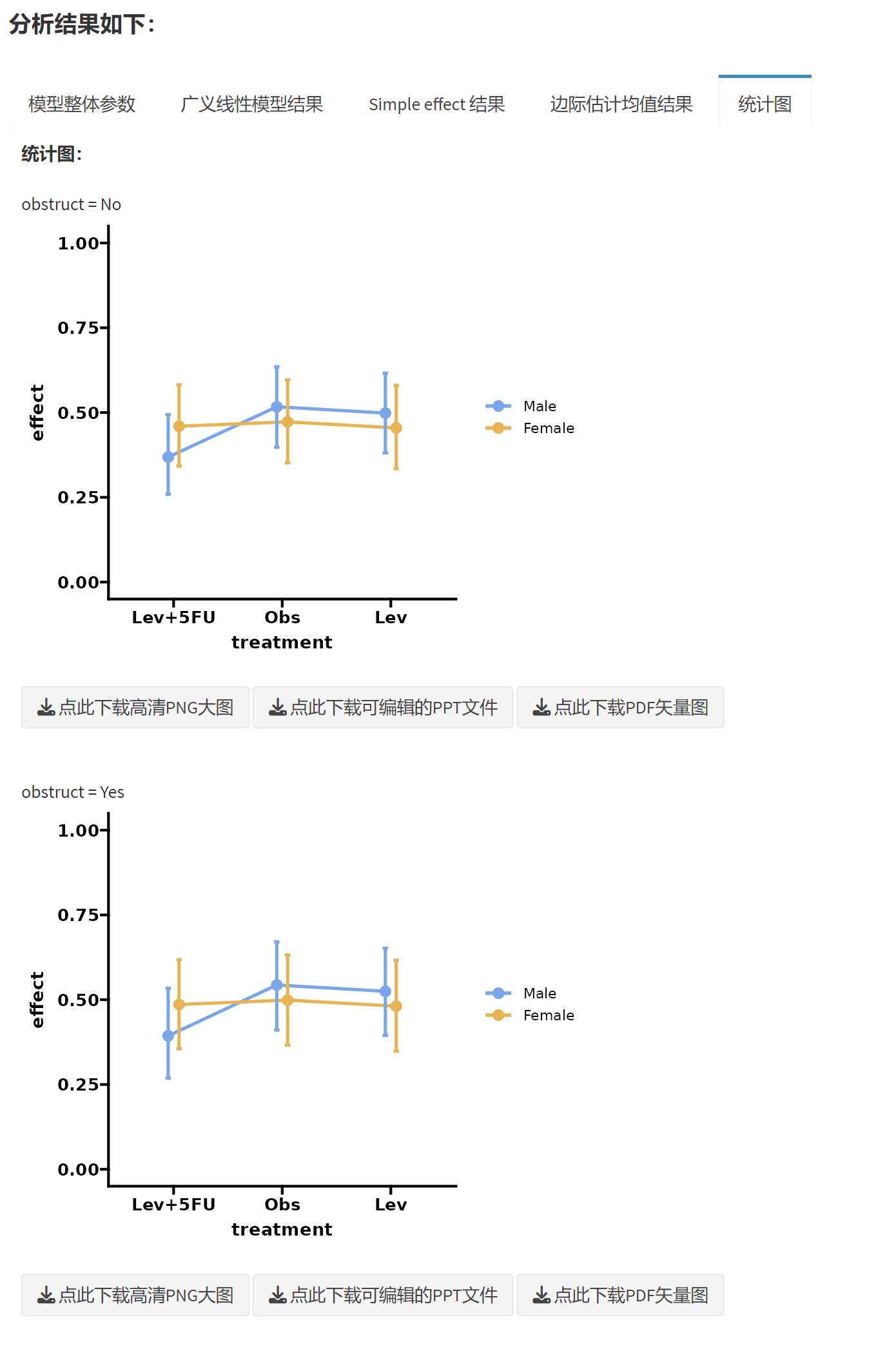
9.21.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
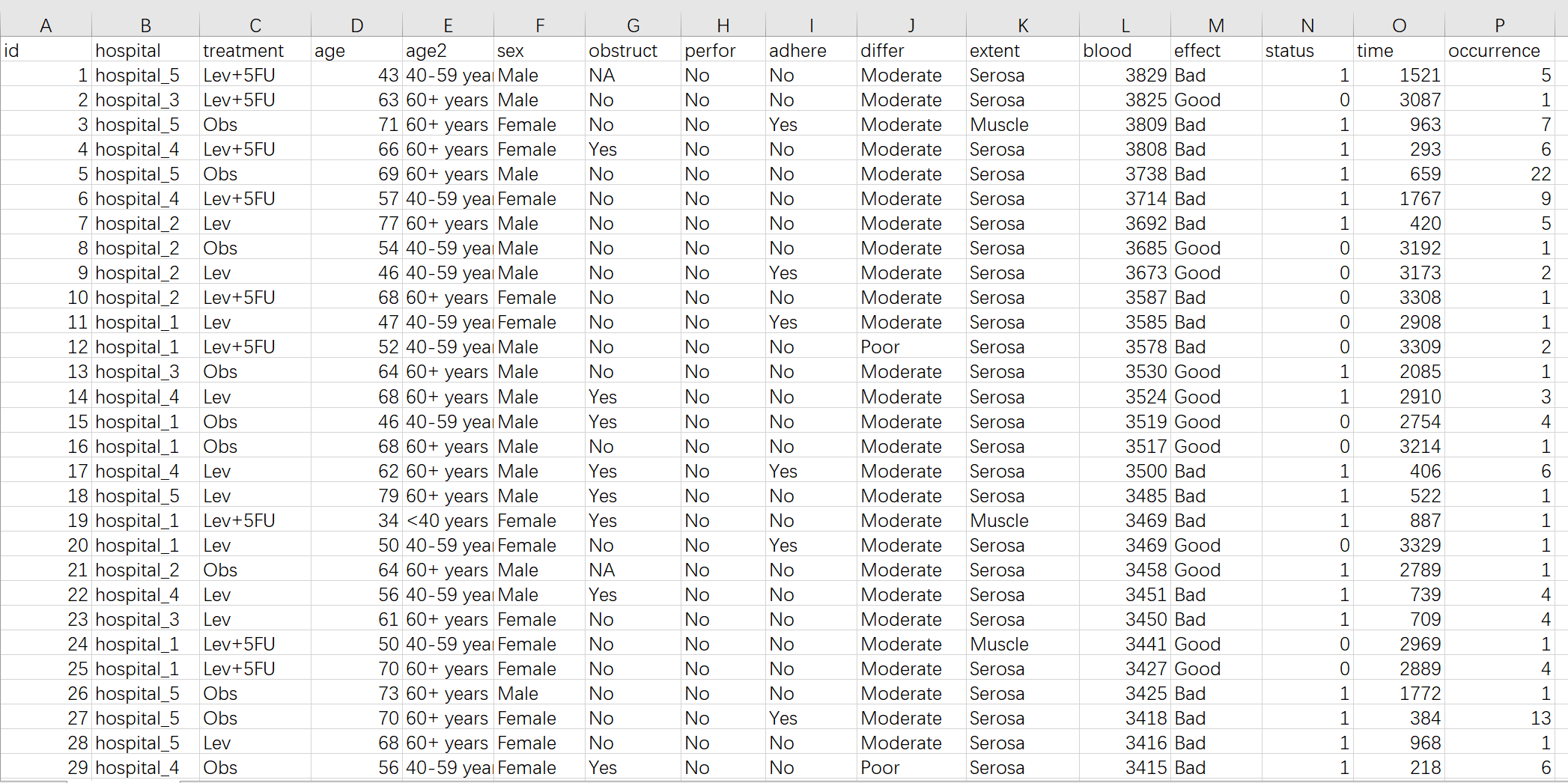
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
每个患者准备两大类数据,自变量和结局(应)变量,自变量和结局分别都可以有多个变量。
如图所示,hospital, treatment, age, age2, sex, obstruct, prfor, adhear, differ, extent 为影响因素(自变量),而blood, effect, occurrence在本例中是结局变量。
自变量有两种,连续性变量(值是连续数据,它可以在变量值所属区间内任意进行取值,如年龄\[岁\]、血糖值、人的身高、智商等)以及分类变量(是说明事物类别的一个名称,其取值是分类数据。如”性别”就是一个分类变量,其变量值为”男”或”女”;“行业”也是一个分类变量,其变量值可以为”零售业”、“旅游业”、“汽车制造 业”等),在本例中 age是连续性变量(numeric), 其他的是分类变量(factor)。age单位为”岁”时为连续变量,而age2为年龄段分组,这时候为分类变量。
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
结局变量在本工具中分为几类:
连续型结局变量
如本例中的blood(某血液检测指标)
二分类结局变量
如本例中的effect(疗效)为二分类变量(Good,Bad)
计数型结局变量
计数型的结局变量为一个非负的整数,如本例中occurrence,是急性发作次数,无法取负数,也不可能取小数。
9.21.3 广义线性模型分析
下一步就是分析啦:
步骤1:选择模型
您需要在”模型选择”框中选择一个统计模型。可选的模型包括线性模型、泊松模型、逻辑斯蒂模型等。如果您选择”自定义”,那么您将可以选择具体的”自定义家族”和”自定义链接函数”。
统计模型是描述变量间关系的数学方程。例如,线性模型假设因变量和自变量之间的关系是线性的;逻辑斯蒂模型常用于处理因变量为二分类的情况;泊松模型则常用于描述计数数据。
“自定义家族”和”自定义链接函数”让您可以选择更复杂的模型。例如,高斯分布(家族)和恒等链接函数(链接函数)构成的模型就是普通最小二乘回归模型。
步骤2:选择因变量
您需要在”请选择结局(应)变量”框中选择一个因变量。因变量也就是您希望通过模型来预测或解释的变量。
可供选择的因变量会根据您之前选择的模型类型自动调整。例如,对于二分类逻辑斯蒂模型,因变量应该是一个二分类变量。
步骤3:选择自变量
在”请点击空白框选择自变量/解释变量”框中,您需要选择一个或多个自变量,即您希望用来预测或解释因变量的变量。这些变量可以根据您的需要进行选择。
步骤4:选择参照类别
对于每一个分类自变量,您需要选择一个参照类别。在模型预测时,其它类别会与此参照类别进行比较。选择参照类别的界面是动态生成的,具体取决于您选择的自变量。
步骤5:选择对比(Contrast)分析的编码
您可能需要为分类自变量选择一种对比分析的编码方式,比如”简单(simple)“、”离差(deviation)“、”哑变量(dummy)“等。这决定了如何在数学模型中表示您的分类变量。
编码方式是统计分析中的重要概念。不同的编码方式会导致模型的解释方式有所不同,但并不会影响模型的预测能力。
步骤7:选择自变量的处理方式
对于连续的自变量,您需要选择一种处理方式,例如”不做处理”、“中心化处理(centered)”、“标准化处理(standardized)”或”进行Log变换”。
这些处理方式可以帮助改善模型的性能和稳定性,或者使模型的参数解释更加容易。例如,中心化可以使得自变量的平均值为0,标准化可以使得自变量的标准差为1,Log变换可以帮助处理右偏的数据。
步骤8:绘制统计图
选择横坐标变量:此处应选择您想要在图形中表示的水平轴的变量,例如性别。
选择区分线条的变量:选择此选项可以使您的折线图中的线条以不同的方式表示,例如表示不同的治疗方法。
选择分层图的变量:这是一个可选项,如果你有一个分层的变量(例如医院),你可以在这里选择它。
步骤8:简单效应(Simple effects)分析
选择 Simple Effects Variable:这是您想要检验其对因变量影响的主要自变量。这通常是您的模型中的主要关注点,您想要了解它如何影响因变量的变化。
选择 Moderator:调节变量是影响自变量和因变量关系强弱的一个变量。也就是说,它可能会改变自变量和因变量之间的关系。
选择 Breaking Variable:分割变量,也就是分层变量,用来将数据集分割成多个部分,以便于在不同的数据子集上进行独立的分析。
步骤9:事后检验(post-hoc tests)
指在收集和分析数据后进行的统计方法,用于比较多个研究组之间的差异。事后检验通常在全局性检验表明存在显著差异之后进行,以确定哪些具体组间比较存在显著差异。
步骤10:边际估计均值(Estimated Mariginal Means)分析
进行边际估计均值(Estimated Mariginal Means)分析:如果你希望进行边际估计均值分析(例如LSMeans等),你可以选中这个选项。
9.22 单组患者生存分析(生存率、中位生存、四种生存曲线)
单组生存分析是一种统计学方法,用于研究生存数据中事件发生的时间和频率。它通常用于描述事件发生的速率、估计生存函数,主要关注单一样本中生存时间的描述性分析。在医学研究领域,单组生存分析常用于研究患者生存期和事件发生的概率,例如研究某种疾病患者的生存期。
以下是一个医学研究中应用单组生存分析的例子:
假设我们要研究某种癌症患者的生存期(时间)。我们可以收集患者的生存数据,包括每个患者的随访时间、是否发生了感兴趣的事件(如死亡)等。利用单组生存分析,我们可以估计患者的生存率及生存期。
在单组生存分析中,Kaplan-Meier(KM)法是一种广泛使用的非参数方法,用于估计生存数据的生存函数。KM法考虑了随访时间的不同长度和不同时间点的失访情况,提供了对生存率和生存期的准确估计。
软件中提供了以下功能:
设置时间变量的单位,如天、周、月、年:方便对生存时间进行度量。
选择统计图表中的时间单位,系统会自动转换:提供不同时间单位的图表展示。
计算平均生存期,中位生存期及其95% CI:提供生存期的估计和置信区间。
计算自定义的各时间点的生存率及其95% CI:可以根据研究需求,查询指定时间点的生存率。
支持生存曲线(Survival Plot):展示随时间推移的生存率变化。
累积事件曲线(Cumulative Events):展示随时间推移的累积事件发生数。
累积风险曲线(Cumulative Hazard):展示随时间推移的累积风险。
KMunicate 曲线(KMunicate-Style Plot):一种直观的方式来展示生存曲线和生存时间的分布。
通过软件的单组生存分析功能,研究者可以更有效地描述和分析生存数据,为临床和公共卫生决策提供有力的依据。

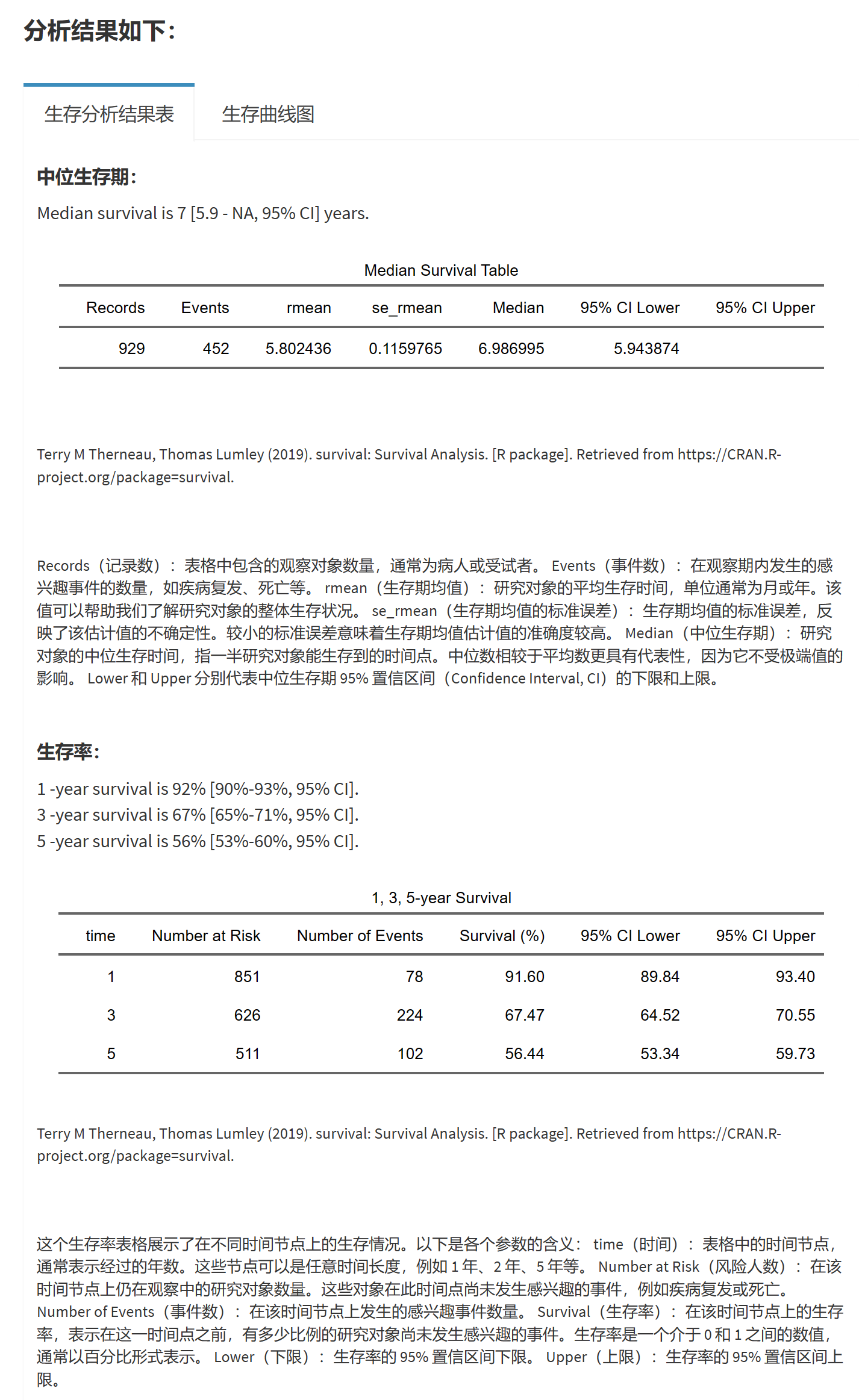
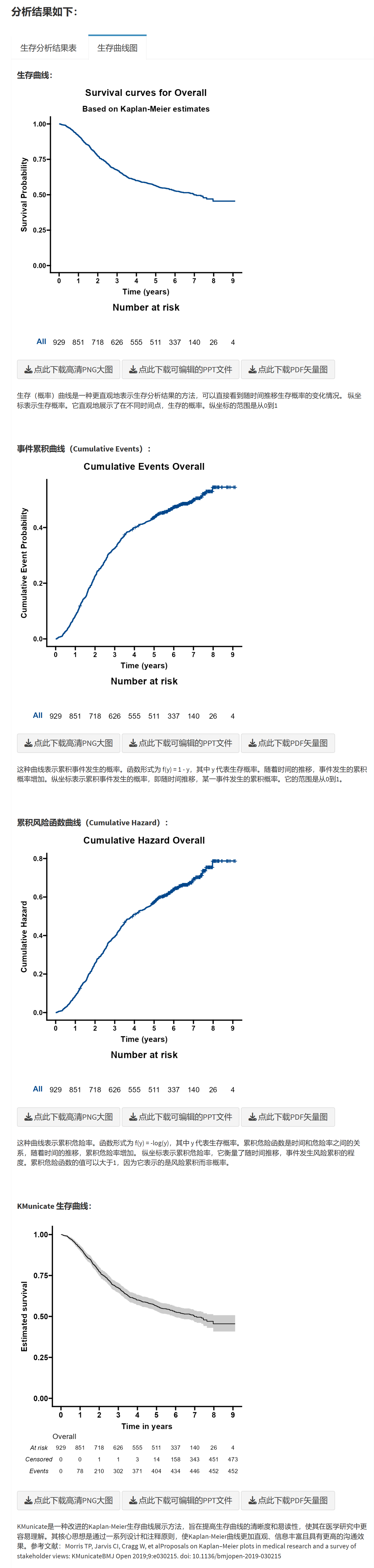
9.22.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
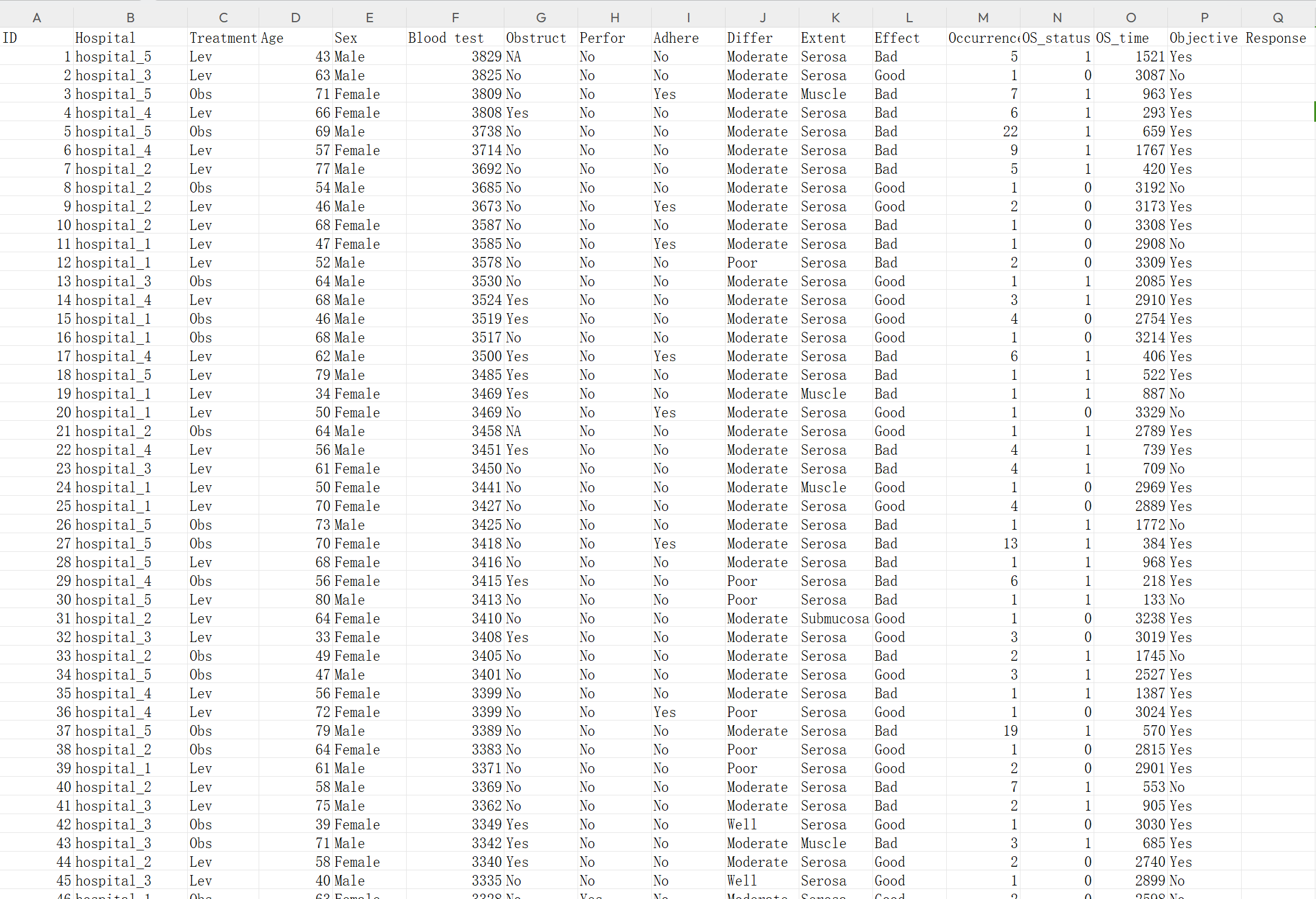
在使用本软件进行单组生存分析之前,您需要准备包含两个关键变量的数据:时间变量(time)和生存状态变量(status)。这两个变量的详细说明如下:
生存状态变量(status):表示患者在研究结束时的生存状态。在本工具中,您可以为status设置任意标签,但为了简单明了,我们建议使用数字 0 或 1。具体而言:
0 代表未观察到感兴趣事件发生(例如患者尚未死亡或失访)。
1 代表已观察到感兴趣事件发生(例如患者死亡,并记录了死亡日期)。 在本软件中,您可以设定哪个标签代表发生事件,确保标签和实际含义相符。
时间变量(time):表示从研究开始日期到观察结束日期的时间差。研究开始日期的定义根据您的研究目的而定,例如随机对照研究通常以随机分组日期为开始,而观察性研究可以选择首次诊断日期或首次治疗日期等。关于time变量,请注意以下事项:
当status为 1 时,观察结束日期为感兴趣事件发生(如死亡)的日期。
当status为 0 时,观察结束日期为最后一次确认患者生存的日期(如研究结束日或随后一次随访日)。
总之,time是一个数值型变量,表示患者从研究开始到观察结束所经历的时间。例如,若time为56,status为1,则表示患者从研究开始到死亡共生活了56天;若time为56,status为0,则表示患者从研究开始到最后一次随访共生活了56天。time的单位可以是天、月或年,本软件可以在分析时进行转换。
在准备数据时,请确保为每个患者填写非负整数的 time 和相应的status标签。time 和 status均不能为空,否则将无法进行分析。若 time 或 status 的数值不确定或缺失,建议不要将该患者纳入数据库。
为了便于理解,我们还是建议在举例时使用 0和 1这样简单的数字标签。当然,在实际操作中,您可以根据自己的需求为status设置合适的标签,比如 “死亡”, “生存或未知(失访)”等标签,然后在软件里把死亡设置为发生事件。只要确保在本软件中正确设定标签含义即可。这将有助于用户更加灵活地应对不同的研究需求,并且更容易地理解和操作数据。
9.22.3 单组患者生存分析
下一步就是生存分析啦:
选择代表时间的变量(如从开始到死亡的时间,或从开始到末次随访时间)。
确定数据中的时间变量每个单位代表的时间长度(天、周、月或年)。
选择代表患者最终状态的变量(只能有两个取值,例如1代表发生事件,0代表删失,如1-死亡,0-存活或未知)。
选择结局变量的水平,以表示发生事件(建模时,选中的水平会设定为1,剩下的水平会设定为0)。
选择后续统计图表中的时间单位(天、周、月或年)。
设置统计表选项:输入需要在统计表中展示的生存率,用英文半角逗号隔开。
设置统计图选项:勾选需要绘制的图表类型(生存曲线、累积事件曲线、累积风险曲线、KMunicate曲线等),并设定图像的宽度和高度。
设定坐标轴的范围:设定横坐标(时间)的上限,以决定曲线完整显示还是部分显示;设定横坐标(时间)的每格单位刻度值。
设置额外图像选项:在图像上显示95%置信区间条带、风险人数表(Risk table)以及删失(censored)数据标记。
点击”开始进行单组生存分析”按钮,程序将根据设置的选项进行分析并生成结果。
请注意,正确设置图像选项(如横坐标上限和最小刻度)有助于让生存曲线显示完整且清晰。
9.23 单组患者归因生存分析(全因死亡率和某种疾病死亡率)
全因生存分析是一种统计方法,主要用于研究从一项研究开始到感兴趣的事件(如死亡)发生的时间间隔。这种分析方法通常会考虑所有可能导致该事件的原因,因此被称为全因生存分析。
归因生存分析则是一种更细分的方法,主要关注由特定原因导致的事件发生的时间和频率。这种方法可以提供更具体的信息,例如,一个病人是由于其疾病导致死亡,还是由于其他非疾病相关的原因导致死亡。
这两种生存分析方法在医学研究中都非常重要。例如,在一个关于某种癌症的研究中,我们可能想要知道患者的整体生存期(全因生存分析),也可能对特定的死因,如由癌症直接导致的死亡(归因生存分析),更感兴趣。
考虑以下医学研究的例子:在一项研究中,研究人员关注某种癌症患者的生存时间。他们收集了患者的生存数据,包括每个患者的随访时间,以及患者是否发生了感兴趣的事件,例如死亡。通过全因生存分析,他们可以估计患者的整体生存时间和生存率。然后,他们可以使用归因生存分析,详细地查看死于癌症的患者的生存时间和生存率,以及由于其他原因导致的死亡的生存时间和生存率。
在进行全因和归因生存分析时,研究者通常需要收集大量的生存数据,包括生存时间,是否发生了感兴趣的事件,以及导致事件的具体原因等。这些数据通常会存在某些特定的模式,例如右偏分布(大多数人在短时间内发生事件,但有少数人会生存很长时间)、存在删失数据(一些参与者在研究结束前失联,导致其生存时间未知)等,这些都是生存数据的特点,需要在进行生存分析时予以考虑和处理。
例如,在全因生存分析中,由于要考虑所有可能的死因,所以往往需要更全面的数据收集和更复杂的数据处理。而在归因生存分析中,研究者需要更仔细地去查看和分析每个发生事件的具体原因,因此也需要更精细的数据处理和更高级的统计方法。
在处理生存数据时,统计软件如MSTATA可以提供大量的帮助。例如,MSTATA可以很方便地处理右偏分布的数据和删失数据,还可以自动进行生存期和生存率的估计,以及生成生存曲线等。此外,MSTATA还能够进行全因和归因生存分析,支持对多种事件结局的处理,如死于疾病(Died Of Disease, DOD)、死于其他原因(Died Of Other Causes, DOOC)、带病存活(Alive With Disease, AWD)和无病存活(Alive Without Disease, AWOD)。
利用MSTATA软件的全因和归因生存分析功能,研究者可以更有效地处理和分析生存数据,更深入地了解研究对象的生存状况,以及各种事件发生的可能性,从而为临床和公共卫生决策提供有力的依据。
以下是MSTATA在处理多事件结局时的一些主要功能:
设置时间变量的单位,方便度量生存时间。
在统计图表中选择时间单位,系统会自动转换。
计算全因和归因的平均生存期、中位生存期以及它们的95%置信区间。
计算自定义时间点的全因和归因生存率及其95%置信区间。
生成全因和归因生存曲线,展示生存率随时间的变化。
显示全因和归因的累积事件曲线,展示累积事件发生数随时间的变化。
生成全因和归因的累积风险曲线,展示累积风险随时间的变化。
此外,MSTATA还提供了KMunicate-Style Plot,这是一种最先进的方式来展示生存曲线和生存时间的分布。

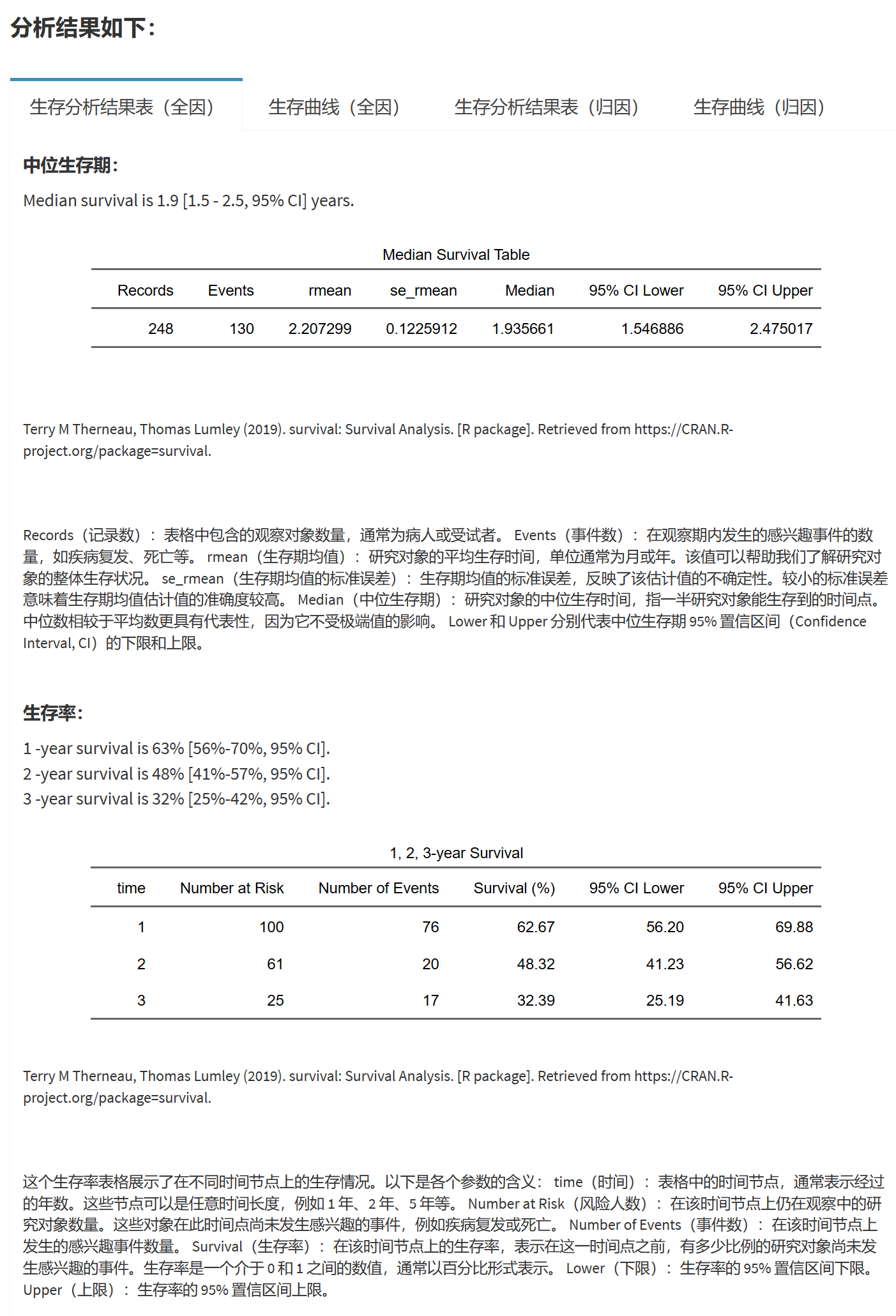
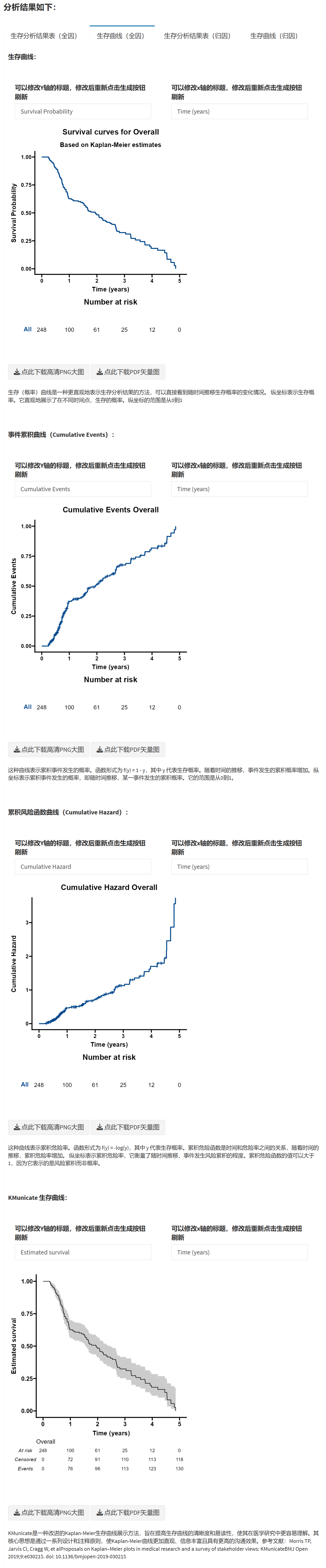
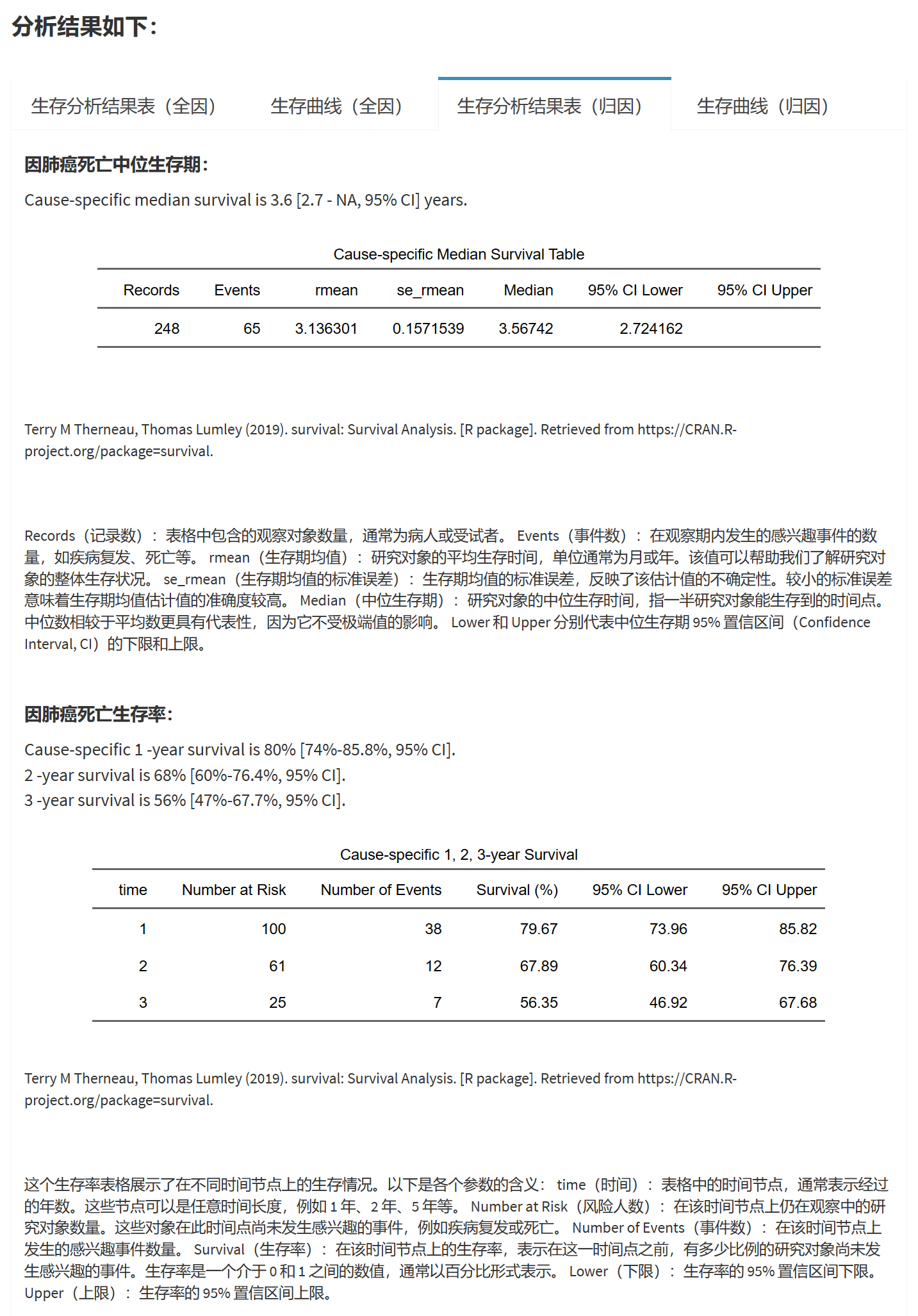
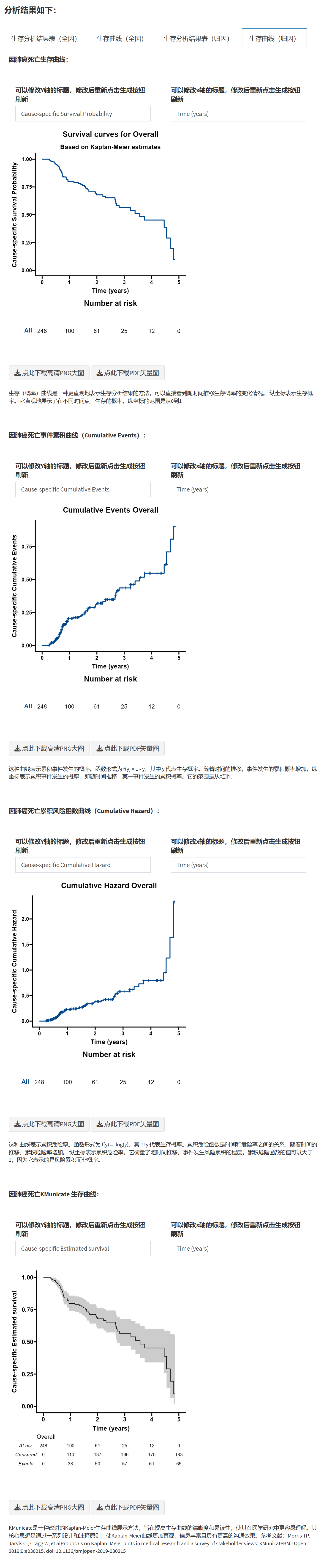
9.23.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
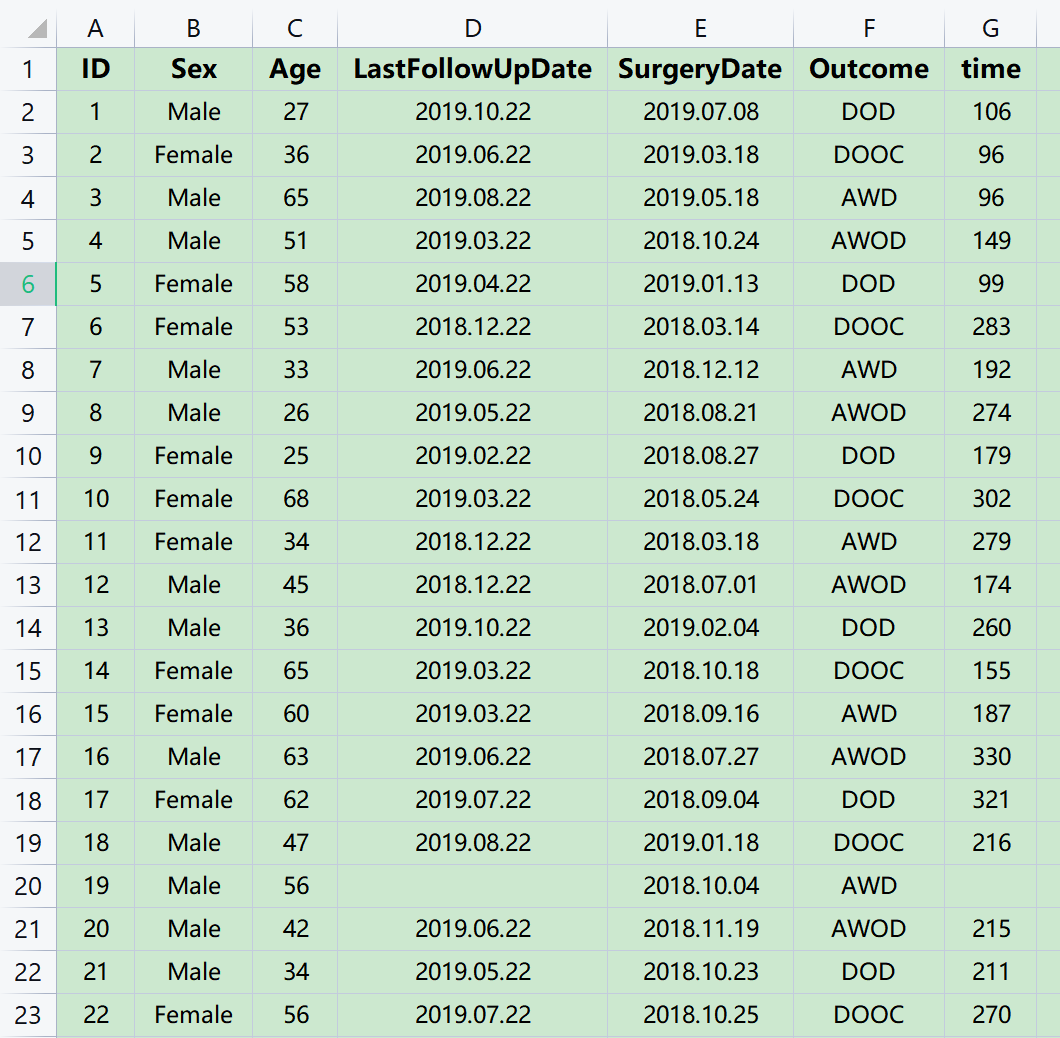
在使用MSTATA软件进行单组生存分析(归因死亡)之前,您需要准备包含两个关键变量的数据:时间变量(time)和生存结局变量(outcome)。这两个变量的详细说明如下:
生存结局变量(outcome):表示患者在研究结束时的生存结局。在本工具中,您可以为outcome设置任意标签,但为了清晰明了,我们建议使用如下标签:死于疾病(Died Of Disease, DOD)、死于其他原因(Died Of Other Causes, DOOC)、带病存活(Alive With Disease, AWD)和无病存活(Alive Without Disease, AWOD)。在MSTATA软件中,您可以设定哪个标签代表发生事件,确保标签和实际含义相符。
时间变量(time):表示从研究开始日期到观察结束日期的时间差。研究开始日期的定义根据您的研究目的而定,例如随机对照研究通常以随机分组日期为开始,而观察性研究可以选择首次诊断日期或首次治疗日期等。关于time变量,请注意以下事项:
当outcome为 DOD 或 DOOC 时,观察结束日期为死亡的日期。
当outcome为 AWD 或 AWOD 时,观察结束日期为最后一次确认患者生存的日期(如研究结束日或随后一次随访日)。
总之,time是一个数值型变量,表示患者从研究开始到观察结束所经历的时间。例如,若time为56,outcome为DOD,则表示患者从研究开始到死于疾病共生活了56天;若time为56,outcome为AWOD,则表示患者从研究开始到最后一次随访并确认无病存活共生活了56天。time的单位可以是天、月或年,MSTATA软件可以在分析时进行转换。
在准备数据时,请确保为每个患者填写非负数的 time 和相应的outcome标签。time 和 outcome均不能为空,否则将无法进行分析。若 time 或 outcome 的数值不确定或缺失,建议不要将该患者纳入数据库。
在实际操作中,您可以根据自己的需求为outcome设置合适的标签,然后在软件里设定对应的事件含义。只要确保在MSTATA软件中正确设定标签含义即可。这将有助于用户更加灵活地应对不同的研究需求,并且更容易地理解和操作数据。
9.23.3 单组患者生存分析
下一步就是生存分析啦:
选择时间变量:在菜单中找到一个下拉菜单,标签为”请选择代表时间的变量”。在这个下拉菜单中,你需要选择代表时间的变量。对于已死亡的患者,这应该是从疾病开始到死亡的时间差。对于尚未死亡或生死未知的患者,这应该是从疾病开始到最后一次随访(即最后一次确认该患者还活着)的时间差。
设定时间单位:在菜单中找到一个单选按钮,标签为”请告诉系统您数据中的时间变量每1个单位代表的时间长度”,你可以在这里选择时间变量的单位,选项包括”天”、“周”、“月”和”年”。
输入疾病名称:在菜单中找到一个文本框,标签为”请输入感兴趣的归因死亡疾病名称”,你需要在这里输入你关注的疾病的名称。
选择结局状态:在菜单中找到一个下拉菜单,标签为”请选择代表患者最终状态的变量”。在这个下拉菜单中,你需要选择代表患者最终状态的变量。这个变量可以有四个值,分别表示死于某种疾病(DOD),死于其他原因(DOOC),带病存活(AWD),无病存活(AWOD)。
选择DOD、DOOC、AWD、AWOD代表的值:在菜单中会有四个下拉菜单,标签分别为”请下拉选择结局变量的哪个水平表示死于某疾病”,“请下拉选择结局变量的哪个水平表示死于其他原因”,“请下拉选择结局变量的哪个水平表示带病生存”,“请下拉选择结局变量的哪个水平表示无病生存”。在这些下拉菜单中,你需要选择相应的值。
选择图表的时间单位:在菜单中找到一个单选按钮,标签为”请选择后续统计图表中的时间单位,系统会自动转换”,你可以在这里选择统计图表的时间单位。
设定统计表选项和统计图选项:在菜单中,你可以设定统计表的生存率、绘制生存曲线、累积事件曲线、累积风险曲线和KMunicate曲线的选项,以及设定图像的宽度和高度。你还可以设定坐标轴的范围,输入数字即可,时间单位默认为前面菜单中选定的输出单位,如年、月、日。
输入生存率:在菜单中找到一个文本框,标签为”请输入您需要在统计表中展示的生存率,用英文半角逗号隔开。“。在这里,你可以输入你想要显示在统计表中的生存率。
设定图像选项:在菜单中,你可以选择是否绘制生存曲线、累积事件曲线、累积风险曲线,以及KMunicate曲线。你还可以设定图像的宽度和高度。
设定坐标轴范围:在菜单中,你可以设定横坐标(时间)的上限(决定曲线完整显示还是部分显示)和横坐标(时间)的每格单位刻度值。
设定其他选项:在菜单中,你可以选择是否在图像上显示95%置信区间条带,是否显示风险人数表(Risk table),以及是否显示删失(censored)数据标记。
开始分析:在菜单的最下方,你可以看到一个按钮,标签为”开始进行单组生存分析”。点击这个按钮,就可以开始进行分析了。
9.24 多组患者生存分析(Log-rank, Cox回归、事后检验、四种生存曲线)
多组生存分析是一种统计学方法,用于研究生存数据中事件发生的时间和频率,并在此基础上进行多组比较。相比于单组生存分析主要关注单一样本的生存时间描述性分析,多组生存分析能更深入地分析不同群体或不同条件下生存数据的差异。
以下是一个医学研究中应用多组生存分析的例子:
假设我们要研究某种癌症患者的生存期,同时也希望比较不同治疗方案的效果(生存时间)。我们可以收集患者的生存数据,包括每个患者的随访时间、治疗方案、是否发生了感兴趣的事件(如死亡)等。利用多组生存分析,我们可以比较不同治疗方案下患者的生存率和生存期。
在多组生存分析中,除了使用 Kaplan-Meier(KM)法估计生存函数,还可引入Log-rank和Cox回归模型来考虑影响生存时间的多个协变量,从而获取更全面的研究结果。
MSTATA统计软件中的多组生存分析模块提供了以下功能:
设置时间变量的单位,如天、周、月、年:方便对生存时间进行度量。
选择统计图表中的时间单位,系统会自动转换:提供不同时间单位的图表展示。
选择分组因素(变量),如治疗方案、性别、年龄等:可以根据研究目的,选择不同的分组因素进行分析。
进行Cox回归分析,计算风险比及其95% CI:提供对影响生存时间的协变量的估计和置信区间。
进行事后检验,两两组间比较生存函数的差异:提供组间生存数据的比较结果。
计算平均生存期,中位生存期及其95% CI:提供生存期的估计和置信区间。
计算自定义的各时间点的生存率及其95% CI:可以根据研究需求,查询指定时间点的生存率。
支持生存曲线(Survival Plot):展示随时间推移的生存率变化。
累积事件曲线(Cumulative Events):展示随时间推移的累积事件发生数。
累积风险曲线(Cumulative Hazard):展示随时间推移的累积风险。
KMunicate 曲线(KMunicate-Style Plot):一种直观的方式来展示生存曲线和生存时间的分布。
提供组间生存曲线比较:在同一图表中展示各组的生存曲线,直观展示组间生存时间的差异。
通过MSTATA软件的多组生存分析功能,研究者可以更全面地描述和分析生存数据,探索和比较不同条件下的生存率和生存期,从而为临床决策和公共卫生政策制定提供更为深入和全面的依据。
9.24.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
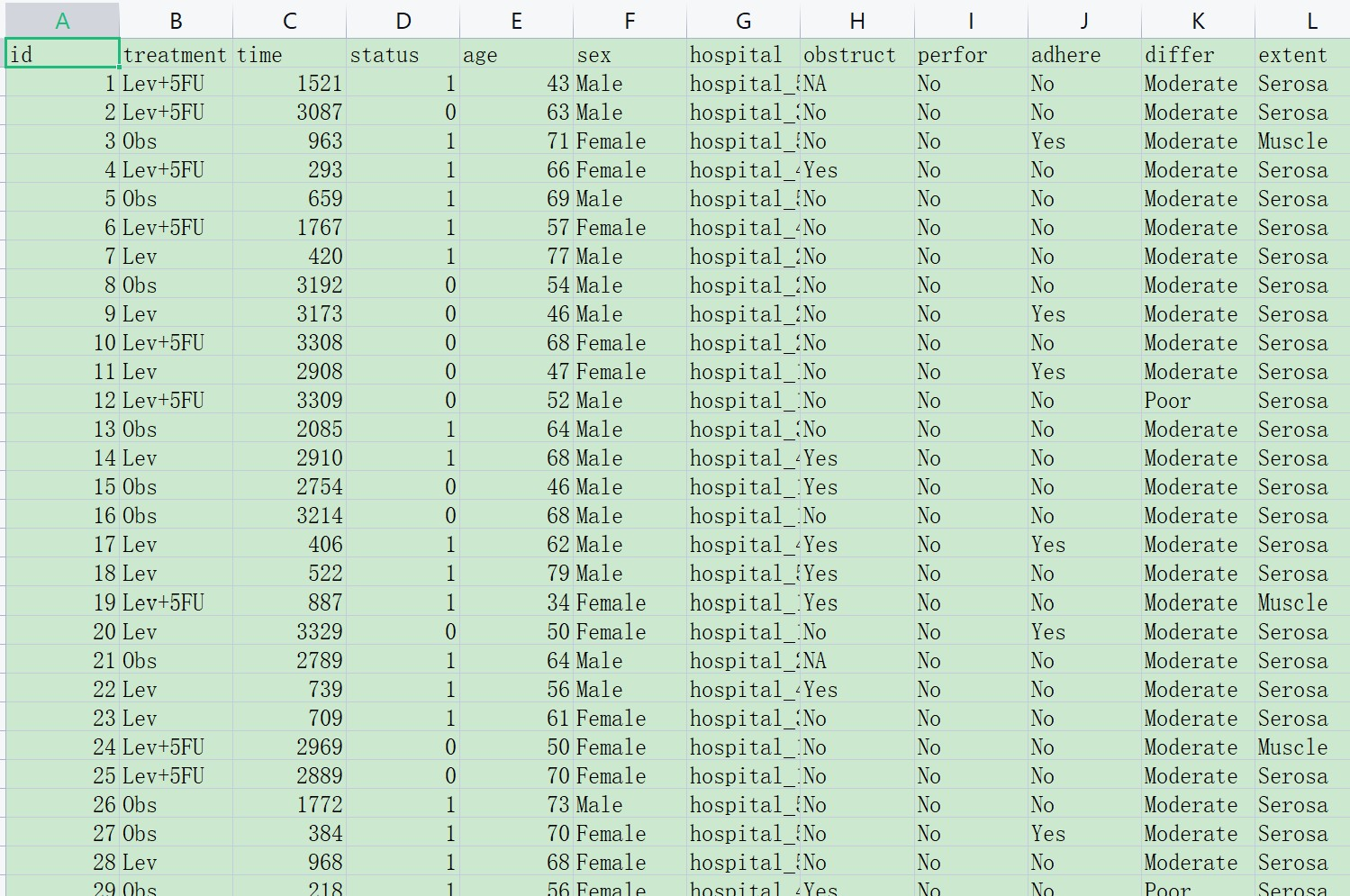
在使用MSTATA软件进行单组生存分析之前,您需要准备包含三个关键变量的数据:分组变量(treatment)、时间变量(time)和生存状态变量(status)。这两个变量的详细说明如下:
代表治疗分组的变量:例如上图中的treatment, 分成了Lev、Obs和Lev+5FU三个组
生存状态变量(status):表示患者在研究结束时的生存状态。在本工具中,您可以为status设置任意标签,但为了简单明了,我们建议使用数字 0 或 1。具体而言:
0 代表未观察到感兴趣事件发生(例如患者尚未死亡或失访)。
1 代表已观察到感兴趣事件发生(例如患者死亡,并记录了死亡日期)。 在MSTATA软件中,您可以设定哪个标签代表发生事件,确保标签和实际含义相符。
时间变量(time):表示从研究开始日期到观察结束日期的时间差。研究开始日期的定义根据您的研究目的而定,例如随机对照研究通常以随机分组日期为开始,而观察性研究可以选择首次诊断日期或首次治疗日期等。关于time变量,请注意以下事项:
当status为 1 时,观察结束日期为感兴趣事件发生(如死亡)的日期。
当status为 0 时,观察结束日期为最后一次确认患者生存的日期(如研究结束日或随后一次随访日)。
总之,time是一个数值型变量,表示患者从研究开始到观察结束所经历的时间。例如,若time为56,status为1,则表示患者从研究开始到死亡共生活了56天;若time为56,status为0,则表示患者从研究开始到最后一次随访共生活了56天。time的单位可以是天、月或年,MSTATA软件可以在分析时进行转换。
在准备数据时,请确保为每个患者填写非负整数的 time 和相应的status标签。time 和 status均不能为空,否则将无法进行分析。若 time 或 status 的数值不确定或缺失,建议不要将该患者纳入数据库。
为了便于理解,我们还是建议在举例时使用 0和 1这样简单的数字标签。当然,在实际操作中,您可以根据自己的需求为status设置合适的标签,比如 “死亡”, “生存或未知(失访)”等标签,然后在软件里把死亡设置为发生事件。只要确保在MSTATA软件中正确设定标签含义即可。这将有助于用户更加灵活地应对不同的研究需求,并且更容易地理解和操作数据。
9.24.3 多组患者生存分析
在MSTATA中进行多组生存分析的步骤如下:
选择代表患者分组的字段:在主界面中,选择分组字段的下拉菜单。例如,如果您正在研究不同治疗方法的效果,您可能会选择”治疗方法”这一字段。如果您希望分组的字段不在列表中,请返回并将其设置为因子类型。
选择事前比较的参照组:在参照组下拉菜单中,选择您希望作为比较基准的组别。
选择代表时间的变量:在时间变量的下拉菜单中,选择代表时间的变量。此时间变量应包括已死亡的患者从开始到死亡的时间差值,和未死亡的/生死未知的患者从开始到末次随访(最后一次活着)时间差值。如果您只有开始和结束的日期变量,没有时间变量,您需要在MSTATA的”生存数据预处理”模块计算时间差值。
设定时间变量的单位:告诉系统您的时间变量每一个单位代表的时间长度,例如天、周、月或年。
选择代表患者最终状态的变量:选择代表患者最终状态的变量,这个变量只能有两个取值,例如1代表发生事件,0代表删失。如果您需要的变量不在列表中,检查原始数据看是否只有两个取值。
选择结局变量的发生事件水平:选择结局变量的哪个水平代表发生事件,系统会在建模时将此级别设定为1,其余级别设定为0。
选择统计图表中的时间单位:系统会自动转换时间单位,例如,可以选择将所有的时间单位转换为年,即1年=365.25天。
设定统计表选项:您可以输入需要在统计表中展示的生存率,使用英文半角逗号隔开。例如,如果您需要展示1年,3年,5年的生存率,可以输入”1, 3, 5”。
设定组间两两比较的选项:可以选择进行事后检验(两两组间比较,有三组及以上时有效),并选择多重比较P值调整方法。
设定统计图选项:您可以选择是否绘制生存曲线(Survival Plot)、累积事件曲线(Cumulative Events)、累积风险曲线(Cumulative Hazard)和KMunicate曲线(KMunicate-Style Plot)。您还可以选择是否在图像中显示Log-rank P值,并设定图像的尺寸。
设定坐标轴的范围:您需要设定横坐标(时间)的上限和单位刻度值。横坐标上限决定了曲线完整显示还是部分显示。设定合适的横坐标上限,可以让生存曲线显示完整,选择合适的最小刻度,才能让图像X轴不堆叠,显示清晰。
设定图像的其他选项:您可以选择在图像上显示95%置信区间条带,显示风险人数表(Risk table),显示删失(censored)数据标记。
以上就是在MSTATA中进行多组生存分析的步骤。这些步骤适用于多种生存分析场景,包括临床试验和观察性研究。每个步骤都可以根据研究的特定需求进行定制。
对上述分析所用统计方法的解释:
Kaplan-Meier法:Kaplan-Meier法(也称生存分析或产品限制方法)是一种用于估计在给定时间点生存概率的非参数统计方法。它在处理”删失”数据(即,一些研究对象在研究结束时仍然存活,我们不知道他们之后何时会发生事件)方面特别有用。KM生存曲线图是一种常见的可视化方法,用来表示生存数据。
Log-rank法:Log-rank检验是一种用于比较两个或更多生存曲线的统计方法。它是一种非参数检验,用于测试不同组之间生存时间的差异是否显著。例如,您可能想比较不同治疗方法的患者生存时间。Log-rank检验的结果是一个P值,如果P值小于您设定的显著性水平(通常为0.05),那么您就可以拒绝零假设(即,所有组的生存时间相同),认为组间的生存时间有显著差异。
Cox回归:Cox回归(也称比例风险模型)是一种用于探索生存时间与一个或多个预测变量(也称协变量)之间关系的统计方法。Cox回归的结果通常表示为风险比(HR),这是一个衡量协变量对生存时间影响程度的指标。例如,如果一个治疗方法的风险比是0.5,那么这意味着接受这种治疗的患者死亡的风险是对照组的一半。
事后两两比较:当我们比较三个或更多的组时,总体比较可能是显著的,但我们可能还想知道哪些具体的组间比较是显著的。这就需要进行事后两两比较。MSTATA软件做两两比较,后台用的是R的
survminer包中的pairwise_survdiff函数,它基于Log-rank检验。注意,由于进行了多重比较,所以我们需要进行P值的调整,以控制第一类错误(错误地拒绝了真的零假设)的概率。这可以使用多种方法,如Bonferroni校正,Holm校正等。
以上就是这些统计方法的基本介绍。在解读这些方法的结果时,一定要考虑到您的研究背景和目标。例如,Cox回归的风险比需要在疾病背景和治疗影响的环境下解读。同时,也要谨慎处理统计显著性和实际(临床)显著性之间的区别。仅仅因为结果在统计上是显著的,并不一定意味着在实际中它就有重要的意义。例如,如果两种治疗方法之间的生存时间差异只有几天,那么即使统计检验结果显著,这种差异在临床上也可能并不重要。
以下是一些基本的解读建议:
Kaplan-Meier曲线:这是生存分析最常见的图形表示。每个曲线代表一个组,Y轴通常表示生存概率,X轴表示时间。曲线的下降表示事件的发生(例如,患者死亡)。如果一条曲线在另一条之上,那么在整个时间范围内,该组的生存概率较高。
Log-rank检验:如果P值小于0.05,那么我们通常会认为生存曲线之间存在显著差异。但是,这并不能告诉我们哪个组更好,也不能量化差异的大小。为此,我们需要查看生存曲线或进行其他类型的分析(例如,Cox回归)。
Cox回归:这种方法的结果通常会给出每个协变量的风险比,以及相应的95%置信区间和P值。风险比大于1表示该协变量增加了事件发生的风险,而小于1则表示降低了风险。置信区间可以告诉我们结果的不确定性,如果它包括1,那么结果就不是统计显著的。
事后两两比较:这些比较的结果通常会给出每对组之间的P值,这些P值通常会经过调整,以考虑多重比较的问题。如果调整后的P值小于0.05,我们通常会认为那一对比较是显著的。但是,和Log-rank检验一样,这并不能告诉我们差异的大小或方向。对此,我们需要查看生存曲线或风险比。
请注意,以上解释并不能涵盖所有可能的场景和结果,所以在解读您自己的结果时,可能需要进一步的专业知识和理解。
9.25 多因素生存分析(包括调整协变量后的生存曲线)
多因素生存分析是一种统计学方法,它可以研究多个因素如何影响事件的发生时间和频率。在临床研究中,这种方法常常被用于研究多个协变量对患者生存时间的影响,例如年龄、性别、治疗方法等。
Cox回归分析是多因素生存分析的一种常用方法,它能够计算每个协变量对生存时间的影响,这种影响常常以风险比(hazard ratio)的形式呈现。在此基础上,我们可以绘制森林图,直观地展示每个协变量的风险比以及其95%置信区间。在森林图中,如果95%置信区间不包含1,那么就说明这个协变量对生存时间有显著影响。
此外,我们还可以生成调整协变量的多因素生存曲线。这种曲线考虑了所有协变量的影响,展示了在控制了其他协变量的影响后,某个特定协变量的不同取值对生存时间的影响。例如,我们可以生成不同年龄组的调整后的生存曲线,来比较不同年龄组的患者的预期生存时间。
MSTATA统计软件为多因素生存分析提供了全面的工具和函数,包括多因素Cox回归分析、生成单因素和多因素森林图,以及调整协变量的多因素生存曲线等功能。这些功能使得研究人员能够方便地进行多因素生存分析,从而更深入地理解各个因素如何影响生存时间。
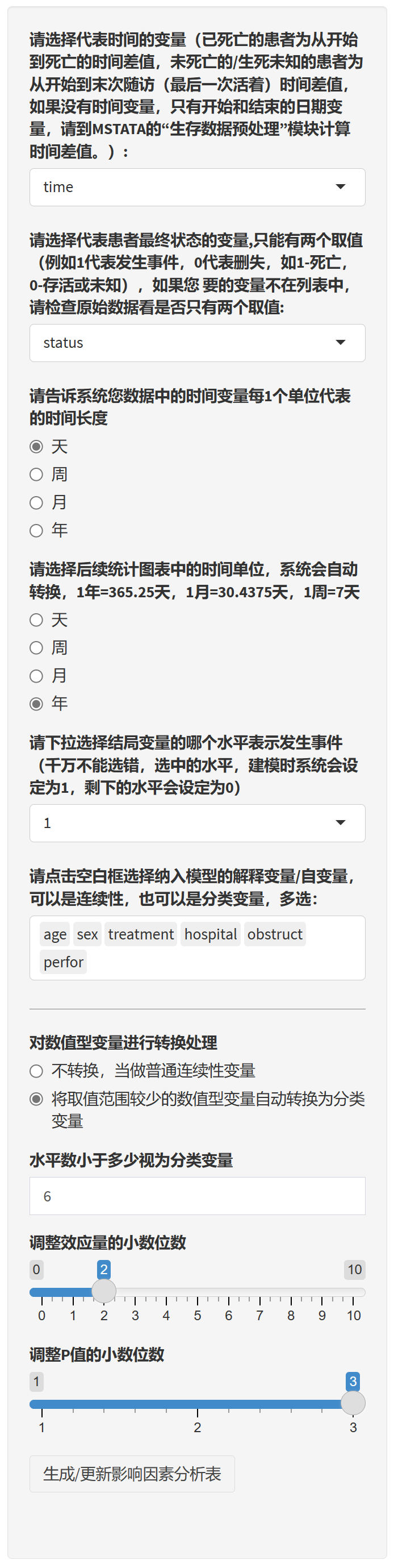
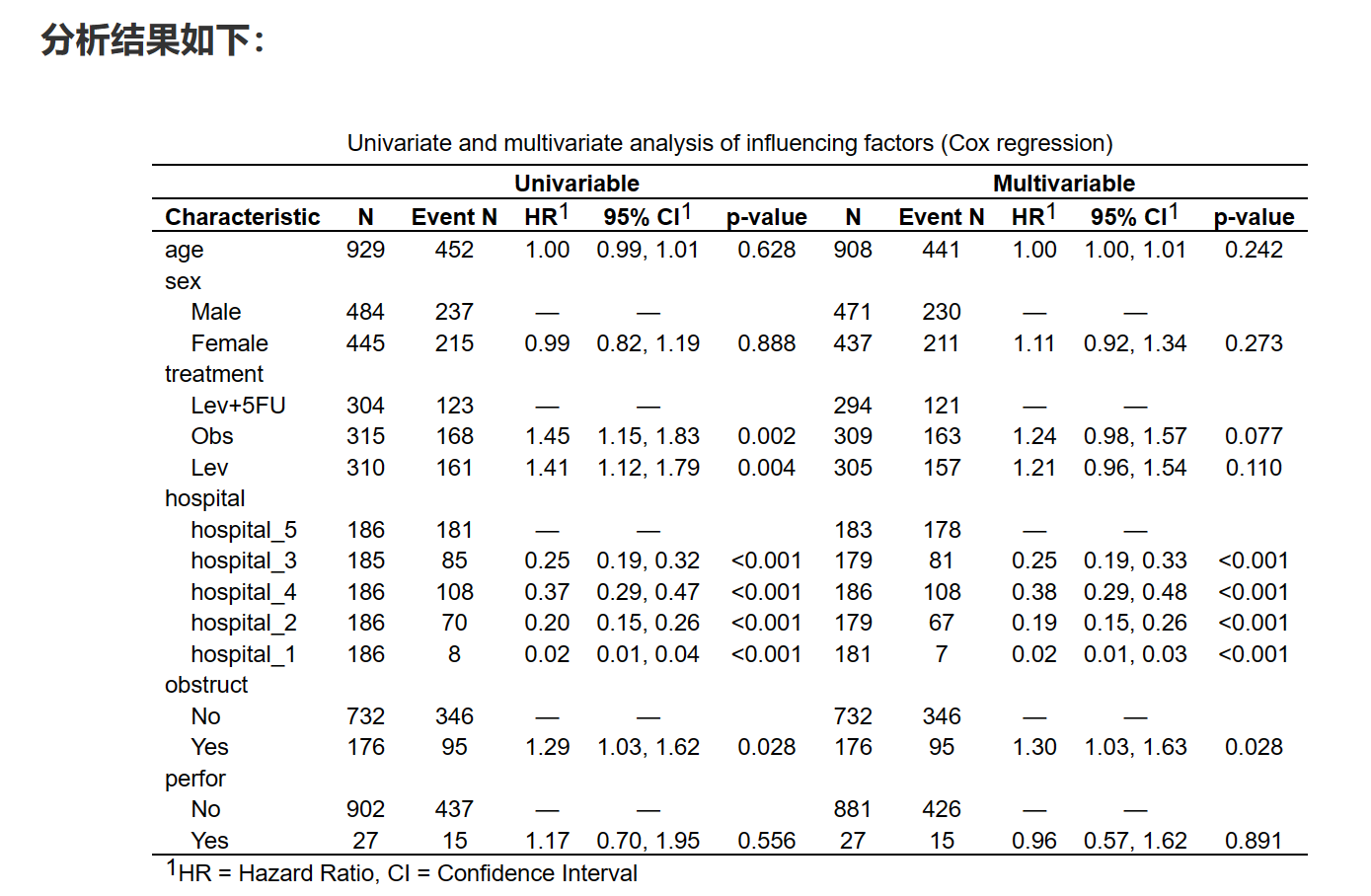
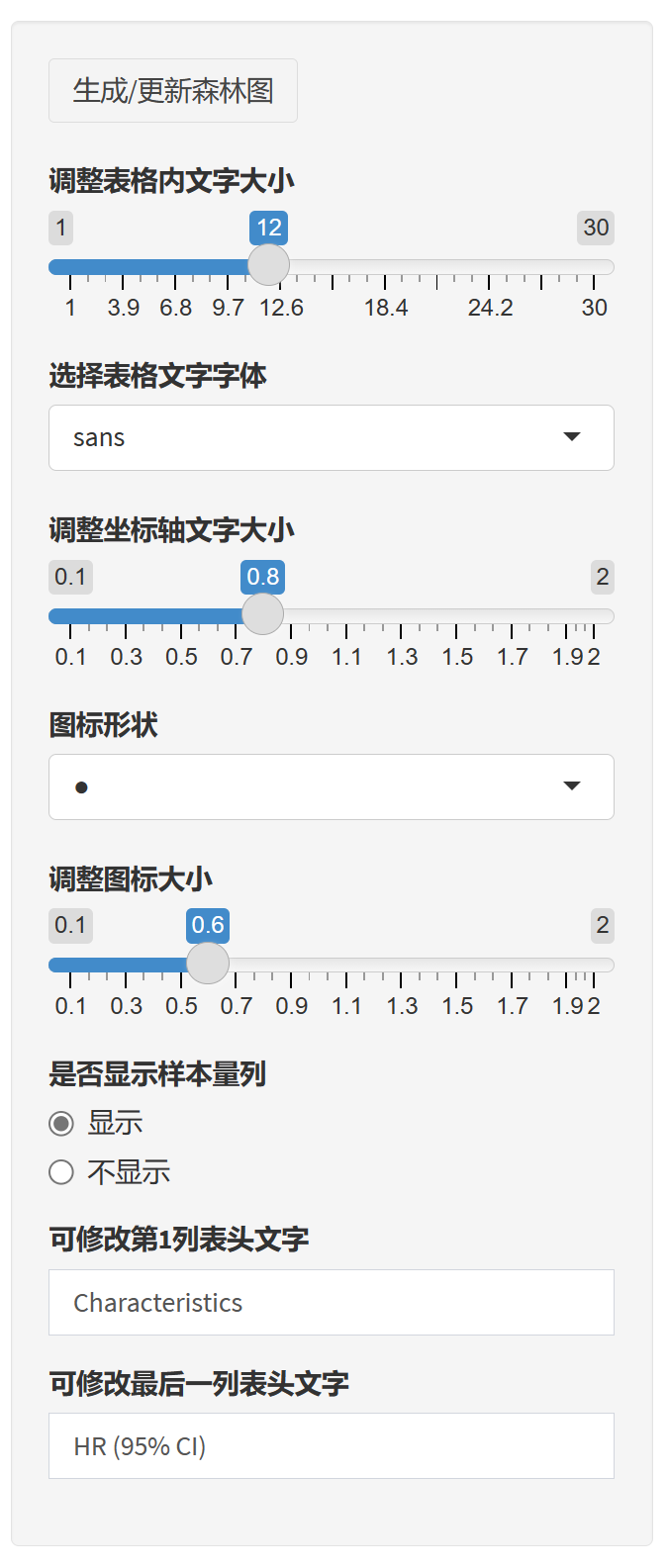
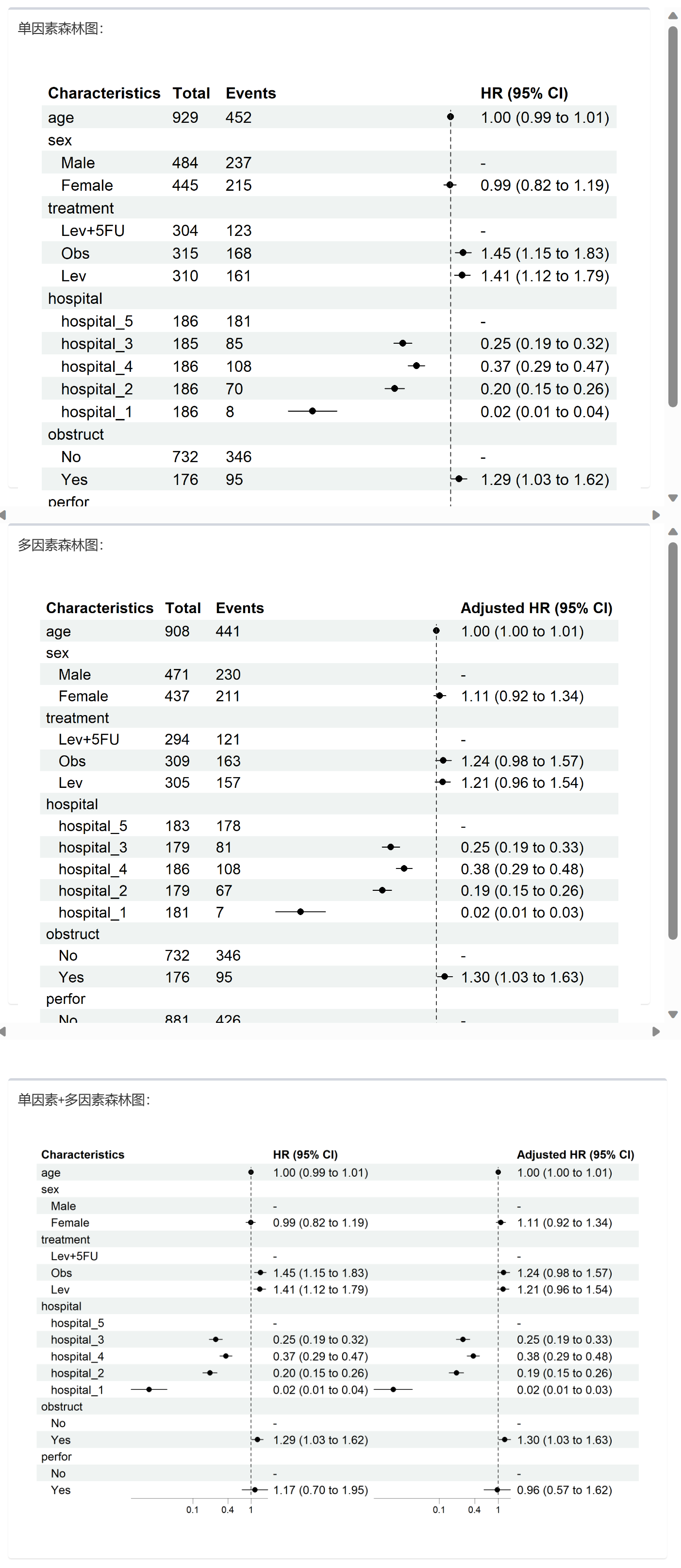
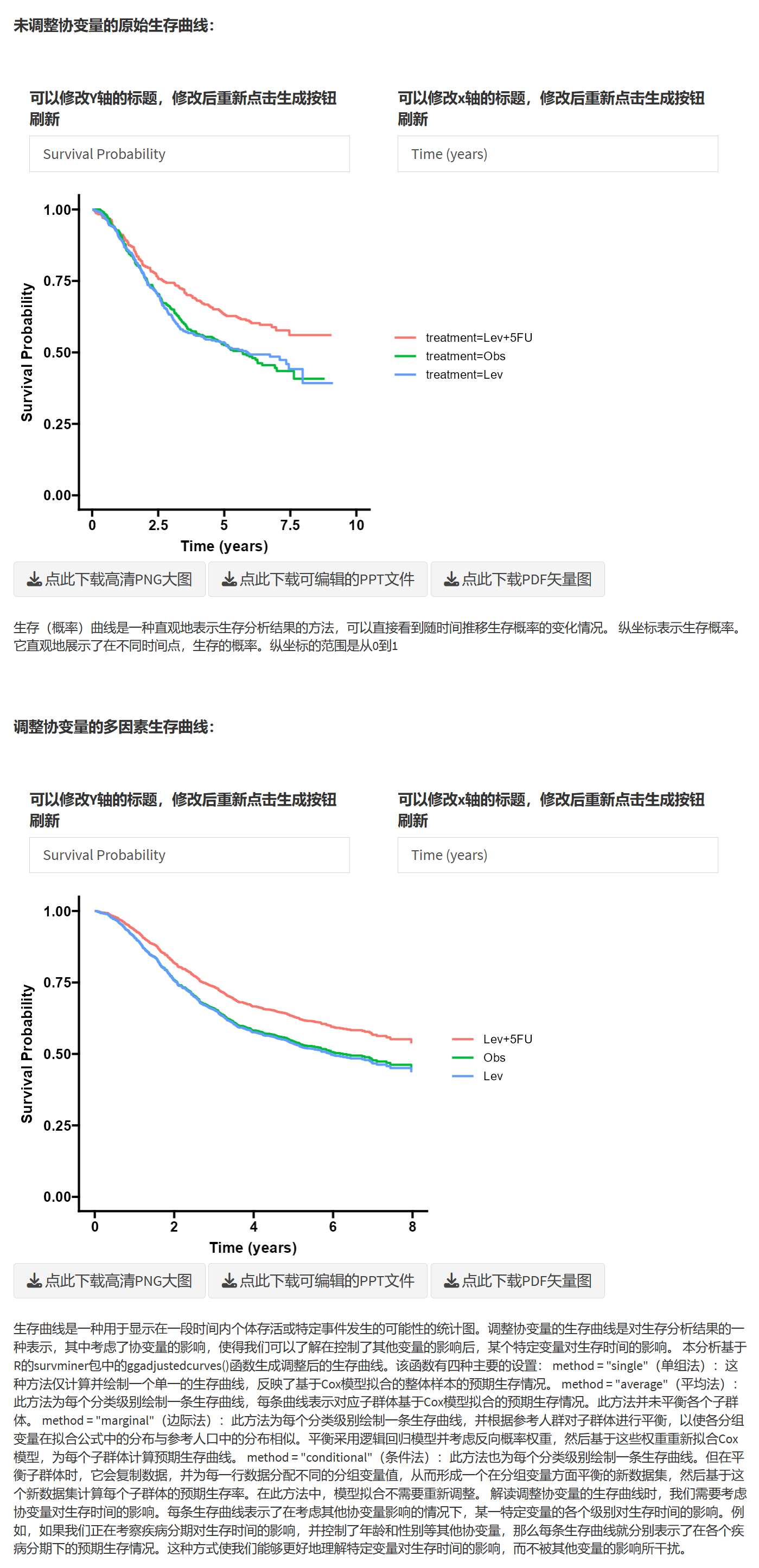
9.25.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
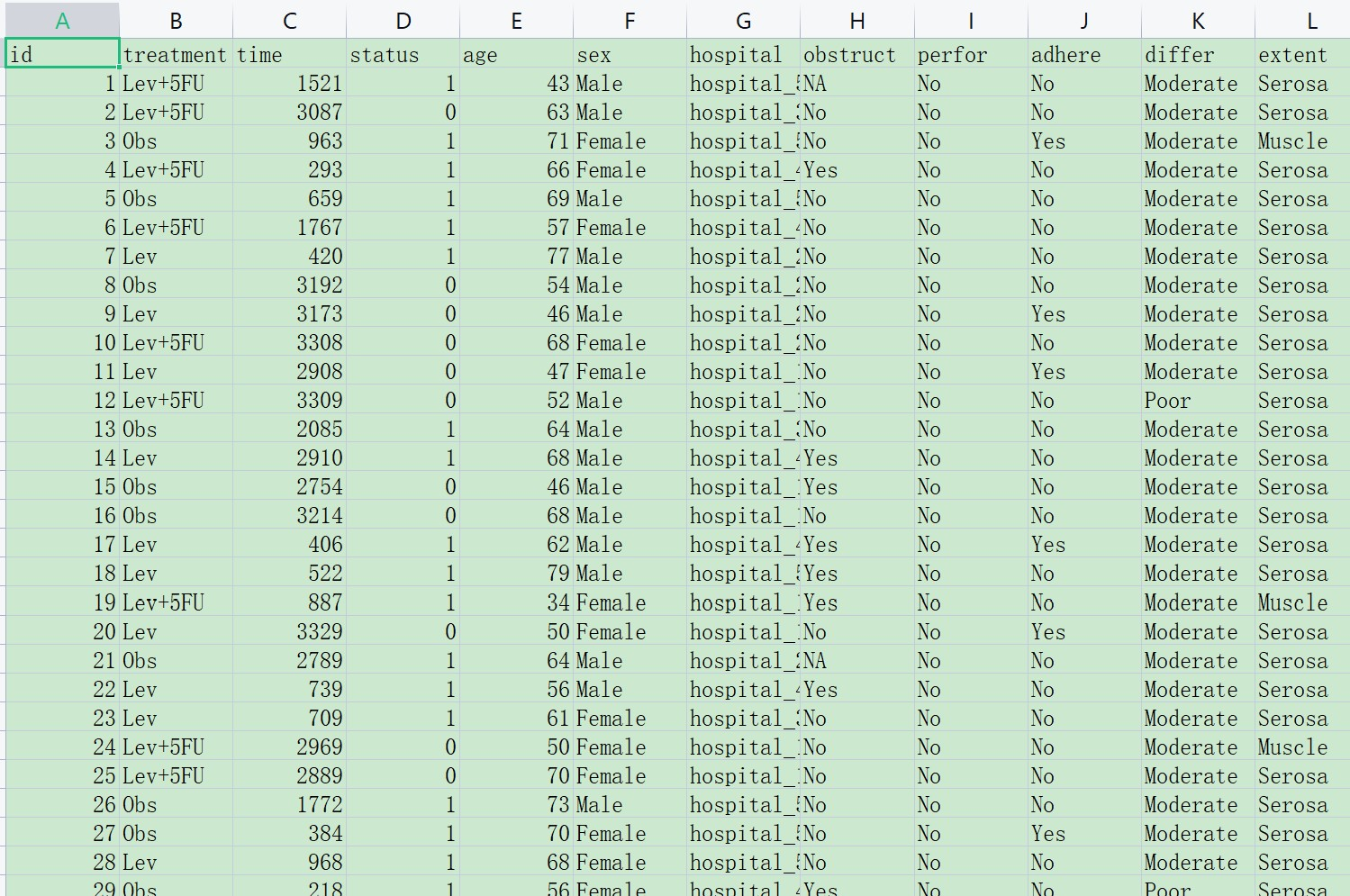
在使用MSTATA软件进行单组生存分析之前,您需要准备包含三个关键变量的数据:分组变量(treatment)、时间变量(time)和生存状态变量(status)。这两个变量的详细说明如下:
生存状态变量(status):表示患者在研究结束时的生存状态。在本工具中,您可以为status设置任意标签,但为了简单明了,我们建议使用数字 0 或 1。具体而言:
0 代表未观察到感兴趣事件发生(例如患者尚未死亡或失访)。
1 代表已观察到感兴趣事件发生(例如患者死亡,并记录了死亡日期)。 在MSTATA软件中,您可以设定哪个标签代表发生事件,确保标签和实际含义相符。
时间变量(time):表示从研究开始日期到观察结束日期的时间差。研究开始日期的定义根据您的研究目的而定,例如随机对照研究通常以随机分组日期为开始,而观察性研究可以选择首次诊断日期或首次治疗日期等。关于time变量,请注意以下事项:
当status为 1 时,观察结束日期为感兴趣事件发生(如死亡)的日期。
当status为 0 时,观察结束日期为最后一次确认患者生存的日期(如研究结束日或随后一次随访日)。
自变量/解释变量,包括性别、年龄、代表治疗分组的变量:例如上图中的treatment, 分成了Lev、Obs和Lev+5FU三个组以及其他协变量
总之,time是一个数值型变量,表示患者从研究开始到观察结束所经历的时间。例如,若time为56,status为1,则表示患者从研究开始到死亡共生活了56天;若time为56,status为0,则表示患者从研究开始到最后一次随访共生活了56天。time的单位可以是天、月或年,MSTATA软件可以在分析时进行转换。
在准备数据时,请确保为每个患者填写非负整数的 time 和相应的status标签。time 和 status均不能为空,否则将无法进行分析。若 time 或 status 的数值不确定或缺失,建议不要将该患者纳入数据库。
为了便于理解,我们还是建议在举例时使用 0和 1这样简单的数字标签。当然,在实际操作中,您可以根据自己的需求为status设置合适的标签,比如 “死亡”, “生存或未知(失访)”等标签,然后在软件里把死亡设置为发生事件。只要确保在MSTATA软件中正确设定标签含义即可。这将有助于用户更加灵活地应对不同的研究需求,并且更容易地理解和操作数据。
9.25.3 多因素生存分析
步骤1:选择时间变量
- 在 “请选择代表时间的变量” 的下拉菜单中选择一个适当的变量。这个变量应该代表已死亡的患者从开始到死亡的时间差值,或者未死亡的/生死未知的患者从开始到末次随访的时间差值。如果您的数据中没有这样的时间变量,只有开始和结束的日期变量,您可以使用 MSTATA 的”生存数据预处理”模块来计算时间差值。
步骤2:选择状态变量
- 在 “请选择代表患者最终状态的变量” 的下拉菜单中选择一个适当的变量。这个变量应该只有两个取值,例如 1 代表发生事件,0 代表删失,如1-死亡,0-存活或未知。
步骤3:选择结局变量
- 在 “请下拉选择结局变量的哪个水平表示发生事件” 的下拉菜单中选择一个适当的水平。请注意不要选择错误的水平,因为选中的水平在建模时系统会设定为1,剩下的水平会设定为0。
步骤4:设置时间单位
- 在 “请告诉系统您数据中的时间变量每1个单位代表的时间长度” 和 “请选择后续统计图表中的时间单位,系统会自动转换” 中,选择适当的时间单位。
步骤5:选择解释变量
- 在 “请点击空白框选择纳入模型的解释变量/自变量” 的下拉菜单中选择一个或多个适当的解释变量。这些变量可以是连续的,也可以是分类的。
步骤6:对数值型变量进行处理
- 在 “对数值型变量进行转换处理” 中,选择是否要将取值范围较少的数值型变量自动转换为分类变量。
步骤7:调整小数位数
- 使用滑块调整效应量的小数位数和 P 值的小数位数。
步骤8:生成影响因素分析表
- 点击 “生成/更新影响因素分析表” 按钮。
步骤9:生成森林图
- 点击 “生成/更新森林图” 按钮。
步骤10:绘制生存曲线
在 “如何进行生存曲线的绘制” 中,选择是按整体人群绘制曲线,还是分组绘制曲线。如果选择分组绘制曲线,还需要选择代表患者分组的字段。
设置图像的宽度和高度。
下面是对调整协变量的多因素生存曲线方法学的解释:
在使用MSTATA的过程中,我们主要使用的是基于R的survminer包中的ggadjustedcurves函数来生成调整后的生存曲线。这个函数是基于Cox比例风险模型(Cox Proportional Hazards Model)来计算和绘制调整后的生存曲线。其主要的理念是为了展示基于Cox模型计算的各个亚群体的预期生存曲线。在Terry Therneau, Cynthia Crowson, Elizabeth Atkinson (2015)的论文’Adjusted Survival Curves’中有关于调整曲线的非常详细的描述和有趣的讨论。该函数目前实现了四种方法:两种非均衡方法,一种条件方法和一种边际方法。
“单一”方法 (“single”):在这种方法下,计算并绘制一个单一的生存曲线,该曲线表示基于Cox模型拟合的全体人群数据计算的预期生存率。
“平均”方法 (“average”):在这种方法下,根据作为变量列表的每一级别,分别计算并绘制一个生存曲线。如果未指定此参数,则会从fit参数的分层组件中提取。每条曲线表示基于Cox模型拟合的数据亚群体的预期生存率。值得注意的是,这种方法下,亚群体并未被平衡。
“边际”方法 (“marginal”):此方法将根据由变量参数选择的分组变量的每个级别绘制一个生存曲线。如果未指定此参数,则会从fit对象的分层组件中提取。子群体将根据fit公式中的变量进行平衡,以使分布类似于参考群体中的分布。如果未指定参考群体,则将整个数据作为参考群体。平衡是以以下方式进行的:(1)对于每个子群体,创建一个逻辑回归模型,模型模拟了考虑fit对象中列出的其他变量后,子群体与参考群体之间的几率,(2)使用到指定子群体的反向概率作为Cox模型的权重,(3)考虑权重的影响,重新拟合Cox模型,(4)根据重新拟合的加权模型,计算每个子群体的预期生存曲线。
“条件”方法 (“conditional”):此方法将对由变量参数选择的分组变量的每个级别绘制一个生存曲线。如果未指定此参数,则会从fit对象的分层组件中提取。平衡子群体的方式是:(1)数据复制的次数与考虑的子群体的数量相同(即k),(2)对于原始数据中的每一行,创建k个副本,并为每个副本分配一个不同的分组变量值,这将创建一个新的在分组变量方面平衡的数据集,(3)根据新的人工数据集,计算每个子群体的预期生存。在这里,模型拟合不会重新进行。
这四种方法都以各自的方式解决了协变量的调整问题,从而提供了更准确的生存曲线预测。选择哪种方法取决于具体的研究目的和数据的特性。不同的方法会给出不同的预期生存曲线,这反映了协变量如何影响生存时间的不同假设。
综上所述,MSTATA通过提供上述四种基于Cox比例风险模型的方法,使用户能够根据他们的具体需求和数据特性选择最适合的方法进行生存曲线的调整。同时,这些方法也使得生存曲线的结果更具有可解释性,可以更清晰地理解协变量如何影响生存时间。
9.26 广义线性混合效应模型(Logistic、Poisson等)
广义混合效应模型是一类非常重要的统计模型,它广泛应用于各种科学研究领域。广义混合效应模型是广义线性模型的推广,它引入了固定效应和随机效应。固定效应通常是我们主要关注并且在所有个体或样本中都相同或者类似的因素,如年龄、性别等。固定效应参数是常数,不随个体或样本的不同而变化。
相反,随机效应则是指影响结果的因素在不同的个体或样本之间具有差异性,这种差异性通常是随机的,无法用固定的数值来描述。随机效应在个体或样本之间是变化的,并且通常假设服从正态分布。
医学中混和效应模型常见的场景有:多水平模型和重复测量模型
1) 多水平模型主要是患者之间有地区聚集性,导致个体之间并不独立,例如多中心研究中,每个中心的患者的环境有相似性,每个不同医生治疗的患者也有相似性。
举例:
在医学研究中,比如我们想研究心脏病的发病率与吸烟、年龄、性别等因素的关系。这些吸烟、年龄、性别就是固定效应,因为我们假设这些因素的效应是在所有个体之间都保持不变的。
然而,如果我们的数据来自不同的医院或者不同的城市,我们可能会考虑到医院或者城市对疾病发生率的影响。这种影响可能是由于各个医院或者城市的医疗条件、生活环境、生活习惯等多种因素造成的。这时,医院和城市就可以被看作是随机效应。我们无法具体衡量每个医院或者城市对疾病发生率的具体影响,但是我们可以假设这种影响在各个医院或者城市之间是存在差异的,并且这种差异是随机的。
因此,通过引入随机效应,广义混合效应模型可以更好地拟合这种数据,并且可以更准确地估计固定效应(如吸烟、年龄、性别)对疾病发生率的影响。
广义混合效应模型可以用于更加复杂的场景,例如研究对象之间存在群体差异(如不同医院的病人、不同地区的居民等)或者观测数据存在时间序列关系(如对同一病人多次进行的观测)等情况。
例如,在医学研究中,我们可能关注某种疾病的发生率是否与特定的风险因素有关,同时考虑到各个医院的影响。此时,我们的因变量是二项分布(患病与否),自变量是风险因素(如年龄、性别、吸烟与否等),随机效应可以是医院(即不同医院可能会对疾病的发生率产生不同的影响)。通过广义混合效应模型,我们可以有效地建立因变量、自变量和随机效应之间的关系,从而更准确地探索特定风险因素对疾病发生的影响。
2) 重复测量模型
在医学研究中,广义混合效应模型通过引入固定效应和随机效应,可以有效处理多次重复测量数据,例如在一年内每月对一组糖尿病患者的血糖水平进行监测。
固定效应是我们关心的、并且在所有个体或样本中都相同或类似的因素,如饮食控制和运动治疗。这些因素是我们想要研究其对血糖水平影响的主要变量。
然而,每个患者的血糖水平并不是只受固定效应影响,他们的基线健康状况、生活习惯、遗传背景等个体特性也会对血糖水平产生影响。同一患者在不同时间的血糖水平测量值之间往往存在一定的相关性,即他们具有聚集性,这是由于他们受到同一个个体特定特性的影响。这种在个体间的测量值的聚集性或相关性,可以通过引入随机效应来进行建模。
具体来说,我们可以假设每个患者都有自己的随机效应,这个效应对该患者所有的测量值都有影响。引入随机效应后,我们就可以在模型中同时考虑到个体间的差异(即随机效应)和治疗效应(即固定效应)。
因此,广义混合效应模型可以更好地处理这种重复测量数据,可以更准确地估计固定效应对血糖水平的平均影响,并且可以更好地预测每个患者在未来的血糖变化趋势。这在医学研究中具有重要的应用价值,对于疾病的治疗和预防提供了重要的参考依据。
MSTATA是一款强大的统计软件,它提供了广义混合效应模型模块,可以用于估计具有类别和/或连续因变量和自变量的广义混合效应模型,还提供了各种选项来方便用户估计交互作用、简单斜率、简单效应等。
MSTATA可以估计多种线性模型,包括固定效应和随机效应模型。公式的写法和R中lme4包相同,例如 (1|hospital) 表示将医院作为随机效应。
MSTATA支持的分布有:高斯分布、二项分布、伽马分布、逆高斯分布。支持的链接函数有:身份、对数、逆函数、逆平方函数。虽然软件不会检查分布/链接函数组合的合理性,但如果数据不符合选定的自定义模型,将会发出错误信息。
MSTATA支持的功能有:设置模型、设置分布、设置链接函数、设置交互作用、设置分类变量参照组、设置连续性变量转换和标化、设置Contrast分析编码、进行事后检验、多重比较P值调整、进行简单效应(Simple effect)分析、进行边际估计均值(LSmeans、事件发生概率等)分析、绘制统计图,以及设置随机效应和固定效应。



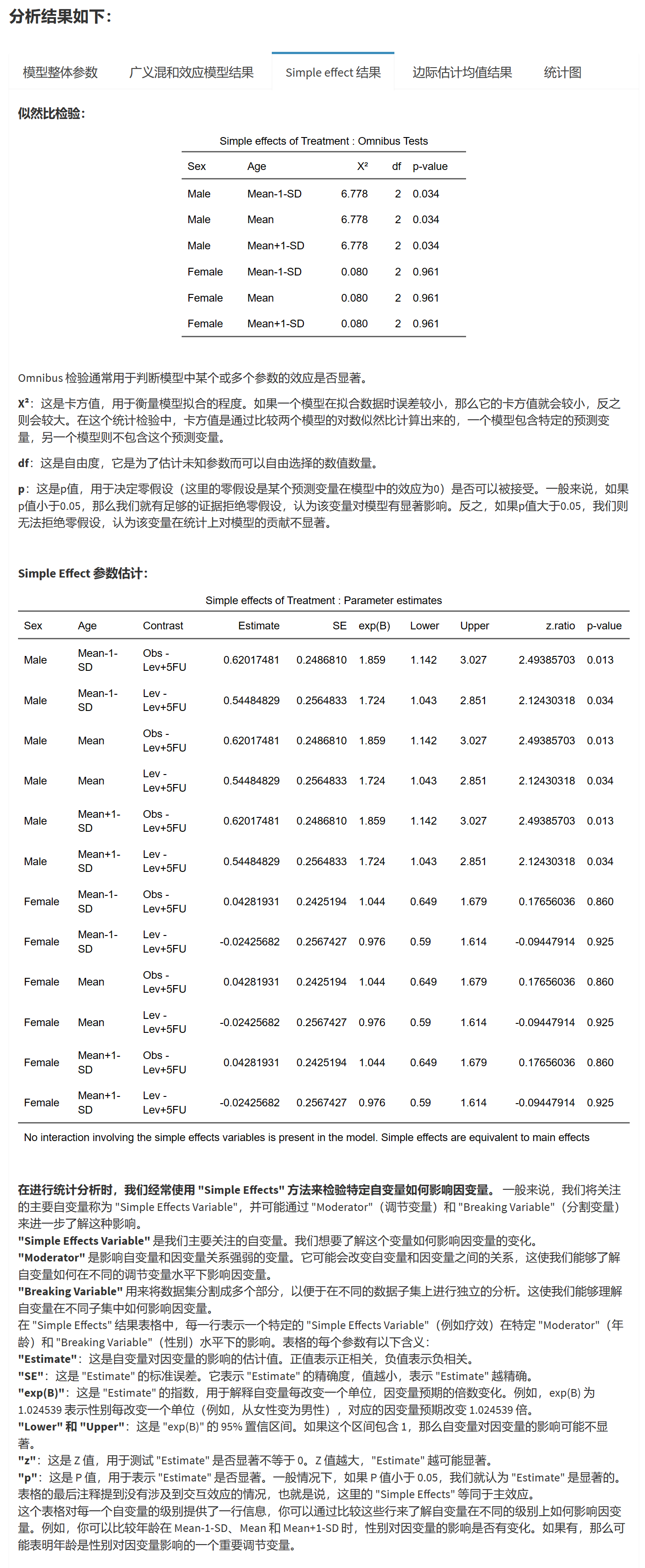
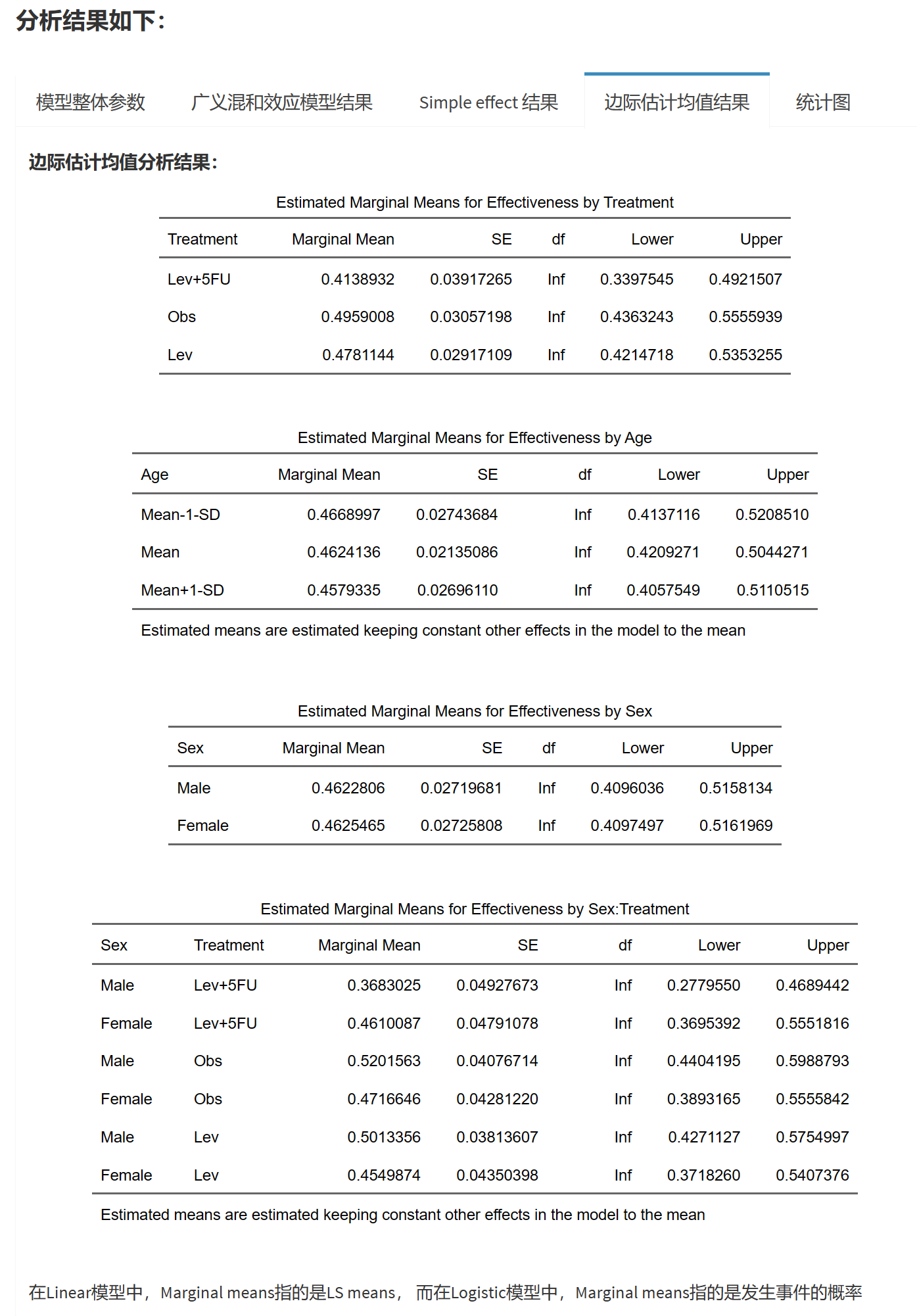
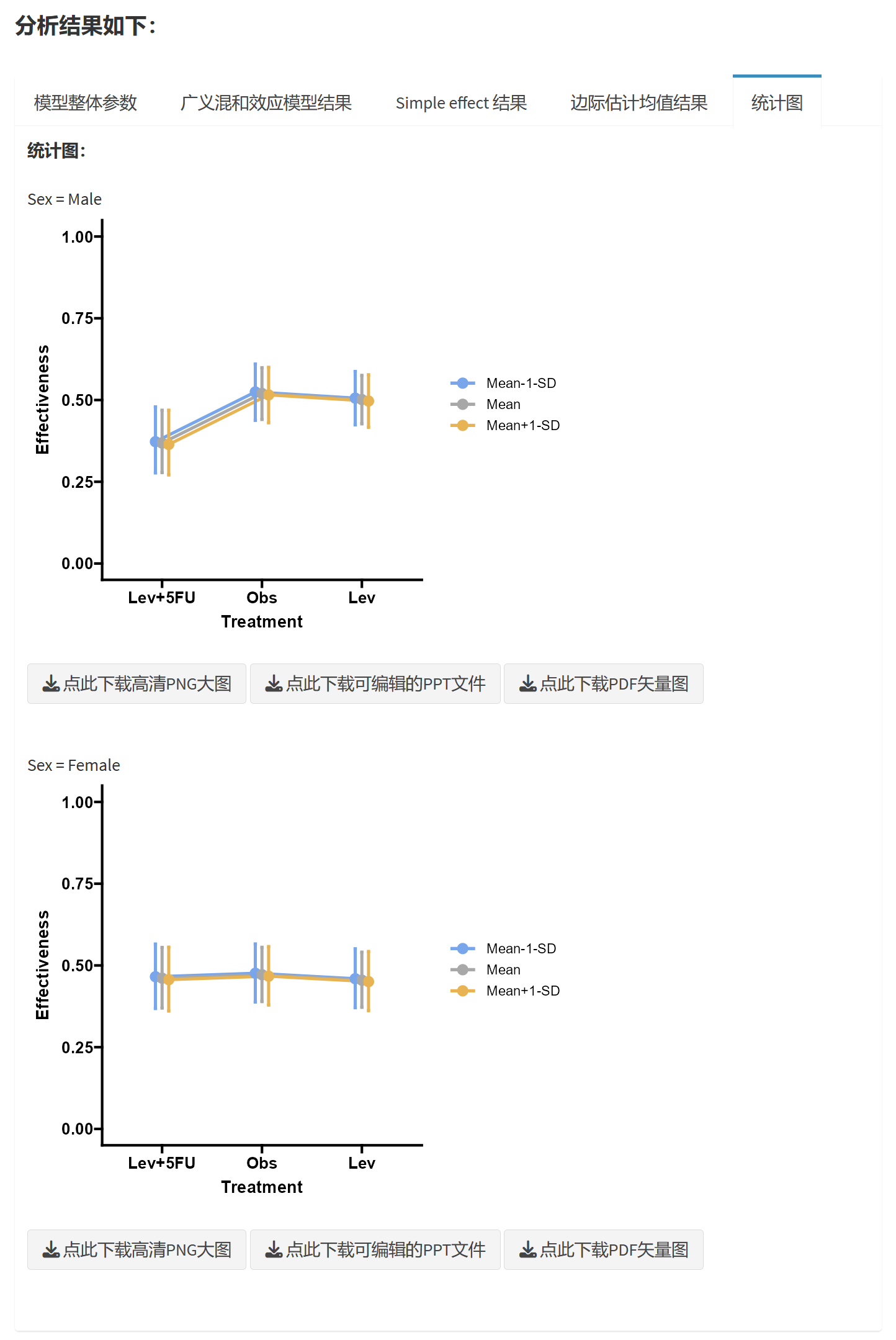
9.26.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
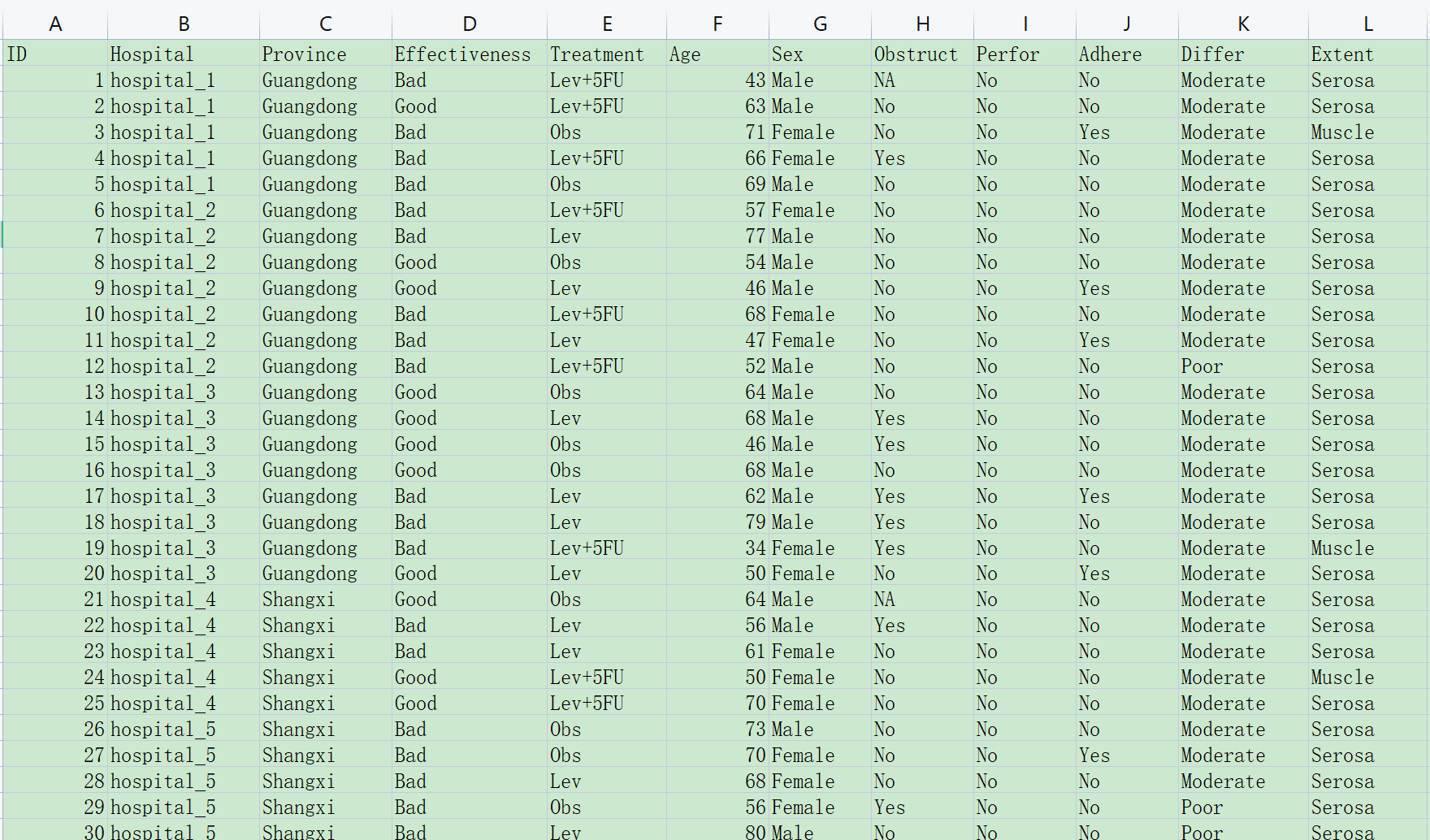
本样例数据的特点:
表示群组(聚集)的变量,如 Hospital
代表结局的应变量:例如上图中的Effectiveness,是一个二分类变量,代表疗效。
解释变量(自变量):例如上图中的Age、Sex、Treatment等等一系列指标,应当设置成固定效应
9.26.3 广义混和效应模型分析
下一步就是分析啦:
步骤1:选择模型
您需要在”模型选择”框中选择一个统计模型。可选的模型包括 Logistic 模型、Probit模型、泊松模型、负二项分布模型等。如果您选择”自定义”,那么您将可以选择具体的”自定义家族”和”自定义链接函数”。
统计模型是描述变量间关系的数学方程。例如,线性模型假设因变量和自变量之间的关系是线性的;逻辑斯蒂模型常用于处理因变量为二分类的情况;泊松模型则常用于描述计数数据。
“自定义家族”和”自定义链接函数”让您可以选择更复杂的模型。例如,高斯分布(家族)和恒等链接函数(链接函数)构成的模型就是普通最小二乘回归模型。
步骤2:选择因变量
您需要在”请选择结局(应)变量”框中选择一个因变量。因变量也就是您希望通过模型来预测或解释的变量。
可供选择的因变量会根据您之前选择的模型类型自动调整。例如,对于二分类逻辑斯蒂模型,因变量应该是一个二分类变量。
步骤3:选择固定效应
在”请点击空白框选择自变量/解释变量”框中,您需要选择一个或多个自变量,即您希望用来预测或解释因变量的变量。这些变量可以根据您的需要进行选择。
另外,还可以选择固定效应间的交互作用项
步骤4:选择群组聚集(Cluster)变量
选择聚集性的群组变量,例如患者ID、医院、省份、国家等,本例选择 Hospital
步骤5:选择随机效应
如果选择了 Hospital,则随机效应的下拉选单里,会出现 Intercept | Hospital, 表示随机截距,还会出现前面选择的固定效应 | Hospital 的选项,表示随机斜率。如果只是校正一下人群在医院的聚集性,因为疗效可能受到医院医生、条件、软硬件的影响,从而疗效不同,但又无法详细探究这些因素(无法在固定效应中定义)时,选择 Intercept | Hospital 就够了,用随机截距模型。
如果在每家医院,治疗方法对结局的影响都不一样(斜率不同),每家医院采用不同的治疗方法疗效可能不同(例如有些医院A疗法就是好,B疗法不好,有些医院则相反),这时候用随机斜率模型,可以把 Treament | Hospital 也选上。如果有些医院就是擅长治疗老年人,年轻人疗效不行,有些医院反过来,这样也可以把 Age | Hospital 也选上。
步骤6:选择参照类别
对于每一个分类自变量,您需要选择一个参照类别。在模型预测时,其它类别会与此参照类别进行比较。选择参照类别的界面是动态生成的,具体取决于您选择的自变量。
步骤7:选择对比(Contrast)分析的编码
您可能需要为分类自变量选择一种对比分析的编码方式,比如”简单(simple)“、”离差(deviation)“、”哑变量(dummy)“等。这决定了如何在数学模型中表示您的分类变量。
编码方式是统计分析中的重要概念。不同的编码方式会导致模型的解释方式有所不同,但并不会影响模型的预测能力。
步骤8:选择自变量的处理方式
对于连续的自变量,您需要选择一种处理方式,例如”不做处理”、“中心化处理(centered)”、“标准化处理(standardized)”或”进行Log变换”。
这些处理方式可以帮助改善模型的性能和稳定性,或者使模型的参数解释更加容易。例如,中心化可以使得自变量的平均值为0,标准化可以使得自变量的标准差为1,Log变换可以帮助处理右偏的数据。
步骤9:绘制统计图
选择横坐标变量:此处应选择您想要在图形中表示的水平轴的变量,例如性别。
选择区分线条的变量:选择此选项可以使您的折线图中的线条以不同的方式表示,例如表示不同的治疗方法。
选择分层图的变量:这是一个可选项,如果你有一个分层的变量(例如医院),你可以在这里选择它。
步骤10:简单效应(Simple effects)分析
选择 Simple Effects Variable:这是您想要检验其对因变量影响的主要自变量。这通常是您的模型中的主要关注点,您想要了解它如何影响因变量的变化。
选择 Moderator:调节变量是影响自变量和因变量关系强弱的一个变量。也就是说,它可能会改变自变量和因变量之间的关系。
选择 Breaking Variable:分割变量,也就是分层变量,用来将数据集分割成多个部分,以便于在不同的数据子集上进行独立的分析。
步骤11:事后检验(post-hoc tests)
指在收集和分析数据后进行的统计方法,用于比较多个研究组之间的差异。事后检验通常在全局性检验表明存在显著差异之后进行,以确定哪些具体组间比较存在显著差异。
步骤12:边际估计均值(Estimated Mariginal Means)分析
进行边际估计均值(Estimated Mariginal Means)分析:如果你希望进行边际估计均值分析(例如LSMeans等),你可以选中这个选项。
9.27 主成分分析
主成分分析(PCA)是一种统计学方法,用于降低高维数据的维数,同时保留数据的主要变异信息。通过将原始数据集的多个相关变量转换为一组不相关的新变量(即主成分),可以更有效地识别和解释数据中的模式。主成分分析广泛应用于多领域,如医学研究、市场分析和财务分析等。
在医学研究中,例如,我们可以用主成分分析来研究一组患者的多个生物标志物数据,以发现这些生物标志物之间的潜在关联,为疾病分类和风险评估提供依据。
MSTATA统计软件的主成分分析模块提供了全面的PCA功能,包括:
适用条件判断:
进行Bartlett’s球形检验,检查数据集是否适合进行主成分分析。
进行KMO抽样适合性检验,评估观测值的数量是否足够。
主成分分析方法:
- 提供旋转(rotation)选项,以便更清晰地解释主成分。
最终提取多少个主成分的方法依据:
基于平行性分析(parallel analysis)选择。
基于特征值(Eigenvalue)选择。
自定义主成分个数。
成分载荷(Loadings):
隐藏低于设定值的成分载荷。
按载荷大小排序。
输出其他统计表:
主成分摘要。
主成分相关性。
初始特征值。
输出统计图:
输出统计图。
绘制碎石图,直观展示主成分的数量选择。
绘制变量贡献图,显示各变量对主成分的贡献。
绘制个体分布图,展示观测值在主成分空间的分布。
绘制双标图,同时展示观测值和变量在主成分空间的分布。
MSTATA的主成分分析模块为您提供了一个强大、全面且易于使用的PCA工具,帮助您从复杂的高维数据中提取有意义的信息。
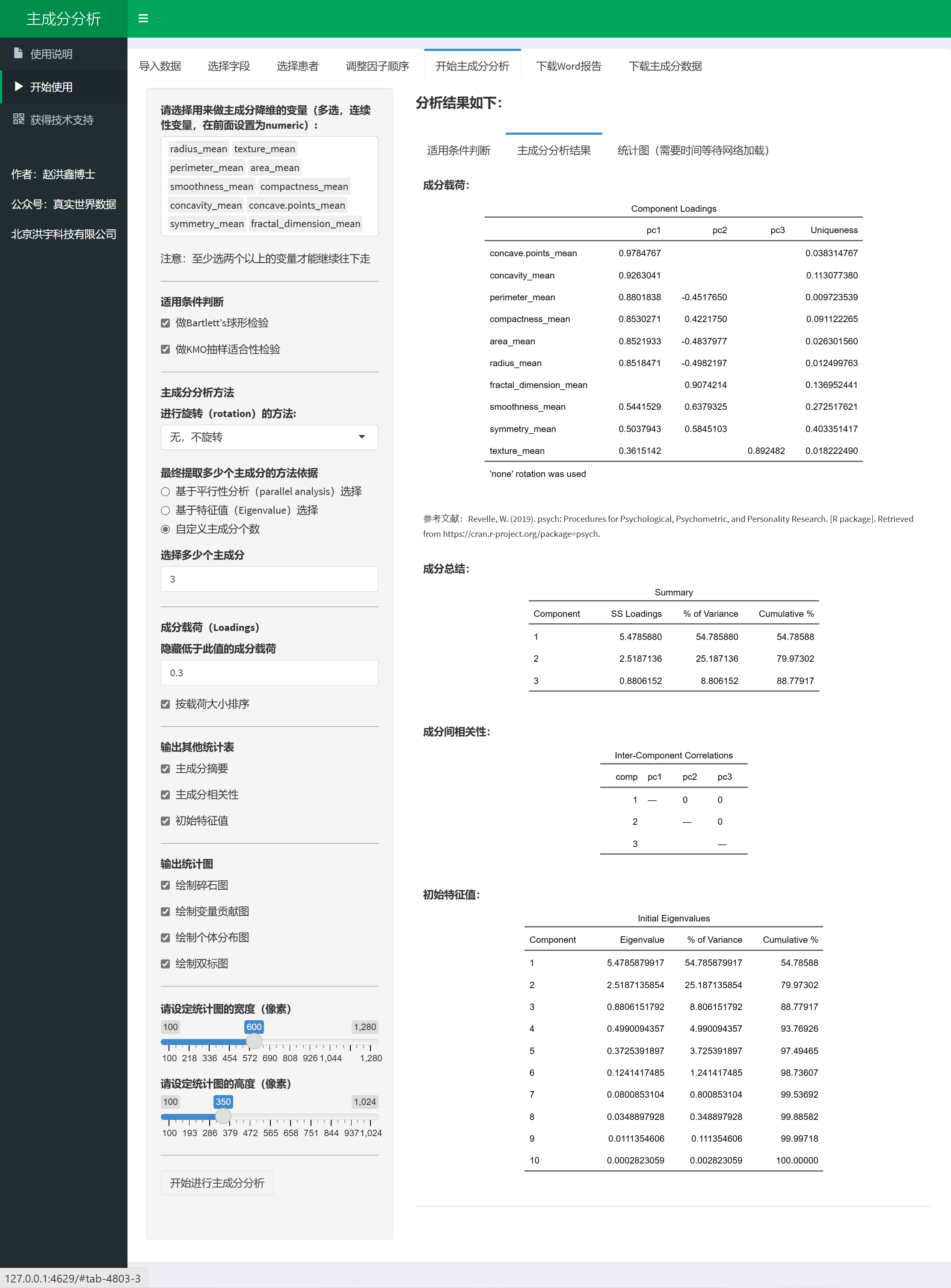
9.27.1 准备数据
首先务必按照下面的格式准备数据(网站上可下载,下载后在此基础上修改):
打开如下图:
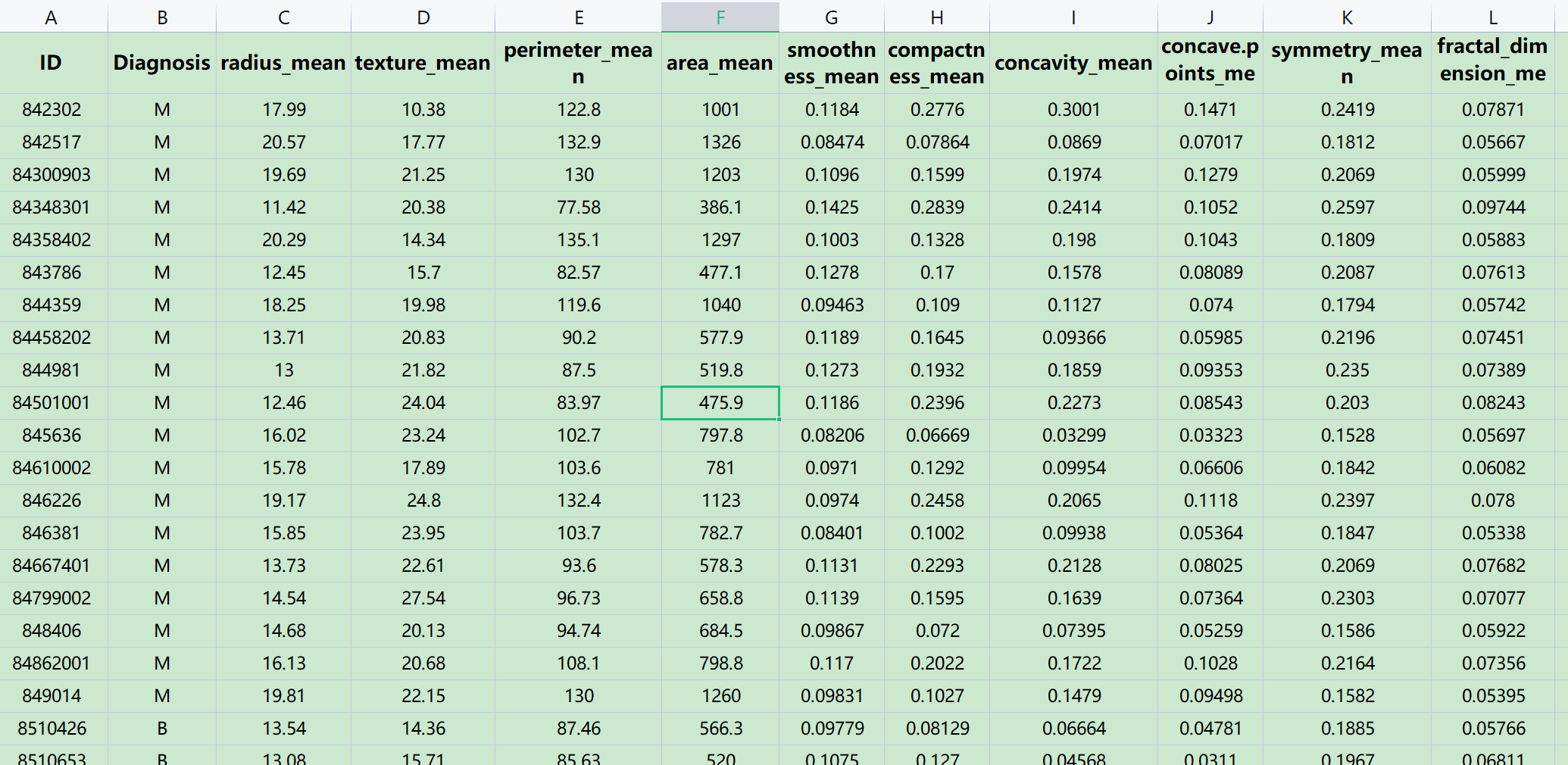
本样例数据的规则:
一个患者一行(这是准备数据最重要的前提)。
分类变量,如diagnosis,不能用来做主成分分析
有相关性的连续性变量,直径,位置,密度等,用来做主成分分析
以上概念很重要,后面有一个页面专门设置连续变量和分类变量。
9.27.3 主成分分析
下一步就是主成分分析啦:
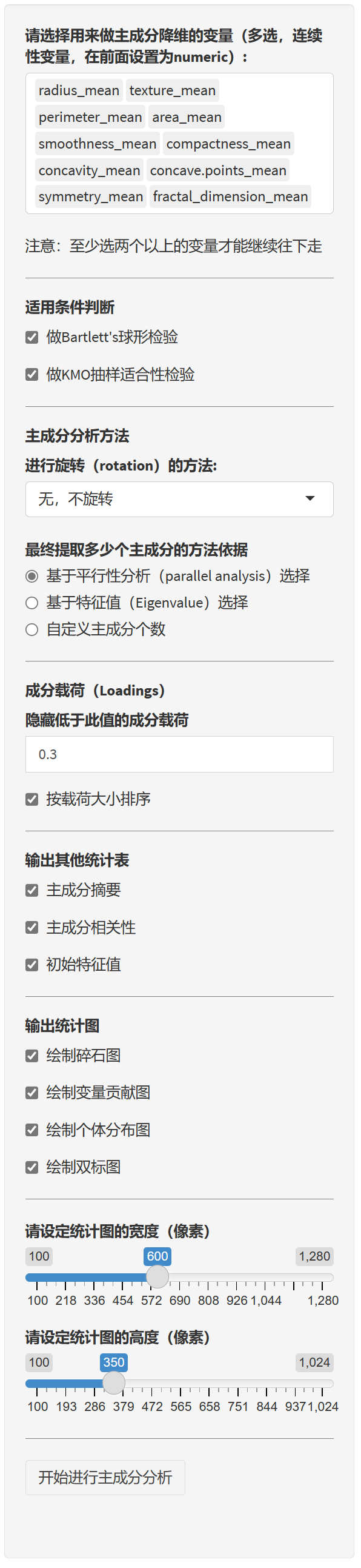
在”选择用来做主成分降维的变量”下拉框中,选择连续性变量(至少选择两个以上的变量才能继续往下走)。
在”适用条件判断”部分,勾选”做Bartlett’s球形检验”和”做KMO抽样适合性检验”,以确定数据集是否适合进行主成分分析。
Bartlett’s球形检验:Bartlett’s球形检验用于检验数据集的协方差矩阵是否为单位矩阵。如果协方差矩阵为单位矩阵,则各变量之间无相关性,不适合进行主成分分析。当检验的P值较小(通常小于0.05)时,我们拒绝原假设(协方差矩阵为单位矩阵),认为数据集适合进行主成分分析。
KMO抽样适合性检验(Kaiser-Meyer-Olkin):KMO检验用于评估数据集的抽样适合性,即各变量之间的相关性是否足够强烈,以便对数据集进行主成分分析。KMO值范围为0到1,值越接近1,表示变量间的相关性越强,主成分分析的结果越可靠。通常,KMO值大于0.6时认为数据集适合进行主成分分析。以下是对KMO值的一般解释:
KMO值大于0.9:非常适合进行主成分分析。
KMO值在0.8至0.9之间:适合进行主成分分析。
KMO值在0.7至0.8之间:较为适合进行主成分分析。
KMO值在0.6至0.7之间:适合性一般,可以进行主成分分析,但需谨慎解释。
KMO值小于0.6:不适合进行主成分分析。
在”主成分分析方法”部分,从下拉框中选择进行旋转(rotation)的方法,如无需旋转、最大方差法、四次方极大法、最优法、斜交法或最简法。
无需旋转(none):在这种情况下,主成分分析不会对主成分进行旋转。这意味着原始主成分将保持不变。无需旋转的主成分分析可以直接反映数据的基本结构,但可能较难解释。
最大方差法(varimax):这是一种正交旋转方法,旨在使主成分的平方载荷在主成分之间的方差最大化。这使得每个主成分都尽可能解释较少的原始变量,从而使结果更易于解释。
四次方极大法(quartimax):这是另一种正交旋转方法,旨在使主成分的四次方载荷在主成分之间的方差最大化。这通常会导致每个主成分解释更多原始变量,但解释性可能较差。
最优法(promax):这是一种斜交旋转方法,先进行正交旋转(通常是 varimax 旋转),然后应用某种幂变换。最优法允许主成分之间存在相关性,并试图使旋转后的载荷矩阵更加稀疏,从而更容易解释。
斜交法(oblimin):这是一种斜交旋转方法,允许主成分之间存在相关性。斜交法试图使每个主成分与尽可能少的原始变量高度相关,从而使结果更易于解释。
最简法(simplimax):这是一种正交旋转方法,类似于 varimax 和 quartimax,旨在使主成分载荷矩阵更加简单。最简法试图使每个主成分只与少量原始变量高度相关,这有助于提高结果的解释性。
在进行主成分分析时,可以根据数据集的特点和需求选择合适的旋转方法。正交旋转方法(如最大方差法和四次方极大法)通常更容易计算和理解,但斜交旋转方法(如最优法和斜交法)可能在某些情况下提供更好的解释性。
在”最终提取多少个主成分的方法依据”部分,选择基于平行性分析(parallel analysis)、基于特征值(Eigenvalue)或自定义主成分个数。
a. 若选择基于特征值(Eigenvalue)选择,设置特征值大于多少时的主成分。
- 若选择自定义主成分个数,设置要提取的主成分个数。
平行性分析(Parallel Analysis):平行性分析是一种基于随机数据模拟的方法,用于确定保留的主成分个数。通过比较实际数据的特征值与随机数据的特征值,确定应保留的主成分数量。具体而言,如果实际数据的特征值大于相应的随机数据特征值,则认为该主成分是重要的,应该保留。平行性分析被认为是在主成分分析中选择保留主成分数量的较为稳健和准确的方法。
特征值(Eigenvalue):特征值是主成分分析中用于衡量主成分解释方差的重要性的指标。在基于特征值的方法中,通常使用”特征值大于1”的准则来确定保留的主成分个数。这意味着,只有那些解释的方差大于原始变量平均方差的主成分才会被保留。然而,这种方法有时会保留过多或过少的主成分,因此它可能不是最稳健的选择方法。
自定义主成分个数:在某些情况下,研究者可能希望根据特定的理论或实践需求来指定保留的主成分个数。这种方法允许研究者根据他们对数据集和研究问题的理解来选择适当的主成分数量。然而,这种方法可能受到主观因素的影响,并且在缺乏理论支持的情况下,可能导致不准确的结果。
在进行主成分分析时,可以根据数据集的特点和需求选择合适的主成分数量选择方法。平行性分析通常被认为是一种较为稳健和准确的方法,而特征值方法和自定义主成分数量方法可能在特定情况下更适用。
在”成分载荷(Loadings)“部分,设置隐藏低于此值的成分载荷,并勾选按载荷大小排序。
成分载荷表示每个原始变量与主成分之间的关系。隐藏低载荷值有助于更容易地识别与主成分密切相关的变量。按载荷大小排序可以帮助用户更直观地了解每个主成分中最重要的变量。
在”输出其他统计表”部分,勾选”主成分摘要”、“主成分相关性”和”初始特征值”。这些选项将在结果中生成额外的统计表,提供更多关于主成分分析的详细信息。
主成分摘要提供了每个主成分的方差解释百分比和累积方差解释百分比等信息。主成分相关性表显示了各个主成分之间的相关性,有助于理解它们之间的关系。初始特征值表显示了每个主成分的特征值,以及与其相关的方差解释百分比和累积方差解释百分比。
在”输出统计图”部分,勾选”绘制碎石图”、“绘制变量贡献图”、“绘制个体分布图”和”绘制双标图”。这些图形可以帮助用户直观地了解主成分分析的结果。
碎石图展示了每个主成分的特征值,有助于确定保留的主成分数量。变量贡献图显示了每个变量对各个主成分的贡献程度。个体分布图描绘了观测值在主成分空间中的位置,以便了解它们在主成分上的分布。双标图综合展示了观测值和变量在主成分空间中的关系,有助于解释主成分在实际问题中的意义。
设置统计图的宽度(像素)和高度(像素)。
点击”开始进行主成分分析”按钮,开始分析。
通过以上步骤,您可以使用MSTATA进行主成分分析,根据您的需求定制化分析过程并输出相关统计表和图形。